10.5. Определение функций Формулы Эйлера.
Известно, что
(1)
(2)
(3)
Положим:
(4)
(5)
(6)
Если
в рядах (4),(5),(6) положить z=x,
то получим соответственно ряды
(1),(2),(3). Это означает, что функции
на
действительной прямой z=x
совпадают соответственно с ранее
определенными функциями
.
Покажем, что функции определены на всей комплексной плоскости. Для этого надо показать, что ряды (4),(5),(6) сходятся во всей комплексной плоскости.
Ряды (4),(5),(6) являются степенными, поэтому нам достаточно показать, что радиусы сходимости этих рядов равны .
Например,
найдем радиус сходимости ряда (4).
Рассмотрим ряд из модулей членов ряда
(4), т.е. ряд
и применим к этому ряду признак Даламбера.
Так как 0<1 для любого Z, то ряд (4) сходится абсолютно, а, следовательно, сходится на всей комплексной плоскости, R= . Аналогично доказывается, что ряды (5) и (6) сходятся на всей комплексной плоскости.
Теперь рассмотрим функцию
Итак,
получена формула
,
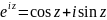которая называется формулой Эйлера.
Из формулы Эйлера можно получить следующие формулы:
Отметим,
что
является четной функцией, а
– нечетной функцией.
.
Пользуясь
формулами Эйлера, можно доказать, что
функция
является периодической с периодом
,
а функции
тоже являются периодическими с периодом
.
Лекция 11
Тема: Комплексные функции. Предел, непрерывность, производная. Аналитическая функция. Условие Коши-Римана.
11.1.Комплексные числа в алгебраической и тригонометрической форме и действия над ними.
Число
z=x+iy,
где х и у действительные числа, а
или
,
называется комплексным числом в
алгебраической форме.
Число
называется
действительной частью комплексного
числа, а
- мнимой частью. Комплексное число
изображается точкой на комплексной
плоскости.
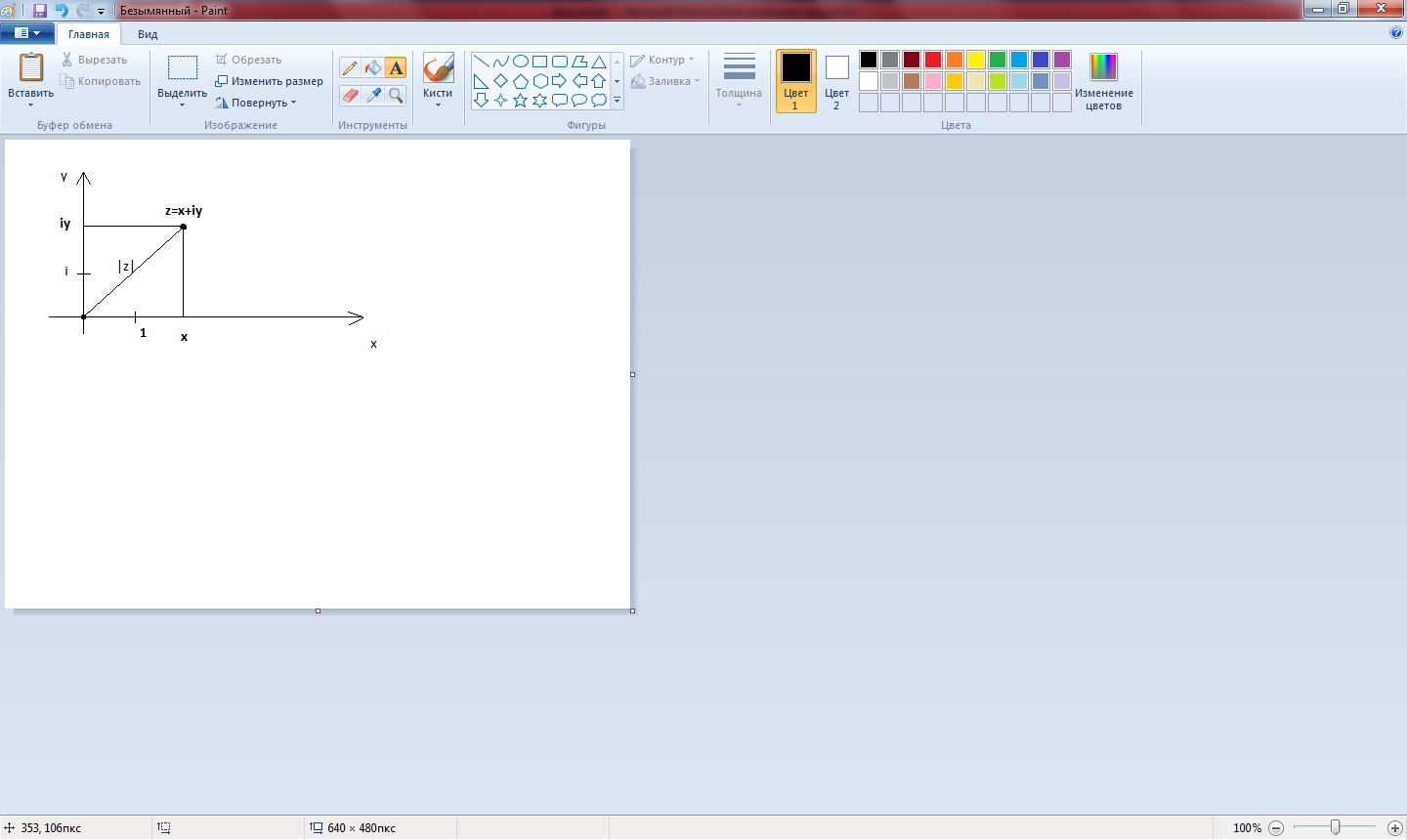
Модуль
комплексного числа есть расстояние от
точки z
до начала координат и обозначается |z|,
.
Сопряженным числом для z=x+iy
называется число
=x-iy.
.
11.2. Действия над комплексными числами в алгебраической форме.
Сложение комплексных чисел.
Умножение комплексных чисел.
Умножение комплексных чисел производится по правилу умножения многочлена на многочлен, учитывая, что .
Деление комплексных чисел.
Тригонометрическая форма комплексного числа.
Пусть z=x+iy.
Рассмотрим полярную систему координат с полюсом в т. О и полярой ОХ. В этом случае формулы перехода от декартовой системы координат к полярной имеют вид:
,
и
комплексное число z
запишется в виде z=
+i
=
,
z=|z|(cos
+isin
)
– Это
и есть тригонометрическая форма
комплексного числа,
.
Модуль
комплексного числа, определяется
однозначно:
а Argz
определен лишь с точностью до любого
слагаемого, кратного 2π. Через argz
обозначается главное значение Argz,
которое является одним из значений
Argz.
Умножение комплексных чисел в тригонометрической форме.
В
частности,
.