Д) Параллель жалғанған қоректендіргіштерді бір балама қоректендіргішпен айырбастауға (түрлендіруге) болады (5-сурет) .

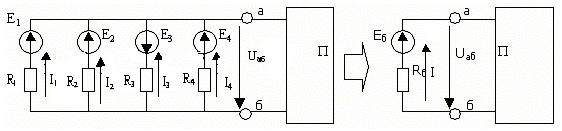
5-сурет

Кирхгофтың бірінші заңы бойынша: I=I₁+I₂+I₃+I₄, немесе

(E_б – U_аб)/R_б =(E₁ – U_аб)/R₁+(E₂ – U_аб)/R₂ +(-E₃ – U_аб)/R₃+(E₄ – U_аб)/R₄. Бұдан

E_б= (E₁G₁+ E₂G₂-E₃G₃+E₄G₄ )/(G₁+G₂+G₃+G₄ ), 1/R_б=1/R₁+1/ R₂+1/ R₃+1/R₄= G₁+G₂+G₃+G₄.

Жалпы жағдайда У_б= /

Электр тізбегінің негізгі принциптері (қасиеттері). 1)Беттестіру принципі: Егер тізбекте бірнеше электр қозғаушы күштер болса, онда осы тізбектің кез келген тармағындағы ток осы электр қозғаушы күштердің сол тармақта әрқайсы тудырған токтарының алгебралық қосындысына тең.

2)Теңгеру принципі: Тізбектің тармағындағы кедергіні сандық мәні сол кедергі мен токтың көбейтіндісіне тең, ал бағыты токтың бағытына қарама- қарсы электр қозғаушы күшімен айырбастауға болады.

3)Өзаралық принцип: Тізбектің k тармағына орналасқан э.қ.к. m тармағында I_m (I_m=E_к ∙G_km) тогын тудырса, онда m тармағындағы э.қ.к. Е_m=E_к k тармағында мәні I_m-ге тең I_k (I_к =E_m ∙G_mk )тогын тудырады. G_km , G_mk -өзаралық өткізгіштіктер.

Қуаттар балансы:Тізбектегі қоректендіргіштердің қуаттарының алгебралық қосындысы сол тізбектегі тұтынушылардың қуаттарының арифметикалық қосындысына тең. Қоректендіргіштің қуаты

Р_қ =E∙I, ал тұтынушы қуаты P_т =I² ∙R формулалары арқылы анықталады.

Потенциалдық диаграмма потенциалдың тізбектің өн бойындағы өзгерісін сипаттайды. Тізбектің бір нүктесінің потенциалын нөлге тең деп алады да, қалған нүктелердің потенциалдарын осы нүктенің потенциалымен салыстыра отырып анықтайды. Абцисса осіне масштаб бойынша кедергілерді салады, ал ордината осінде потенциалдарды көрсетеді.

Негізгі әдебиеттер: [1(21-24, 33-35, 42-54), 3(71-74, 80-91, 94-96, 104-108)]

Қосымша әдебиеттер: [ 4,5,7,8]

Бақылау сұрақтары:

1.Бір э.қ.к-і бар электр тізбектерін есептеу. Балама түрлендіру тәсілі. Кедергілердің бірізді, параллель және аралас жалғануы.

2.Кедергілердің жұлдызша және үшбұрыштап жалғануы.

3.Э.қ.к-тердің бірізді және параллель жалғануы. Балама генератордың параметрлері.

4.Электр тізбегінің негізгі принциптері

5.Қуаттар тепе-теңдігі. Потенциалдық диаграмманы құру.

№3 Дәріс. Тұрақты токтың бірнеше э.қ.к.-тері бар күрделі тізбектерін есептеу тәсілдері. Кирхгоф заңдарын пайдалану арқылы есептеу тәсілі. Контурлық токтар тәсілі. Түйіндік потенциалдар тәсілі

Тұрақты токтың күрделі тізбектерін есептеу үшін мынандай тәсілдерді қолдануға болады:

1) Кирхгофтың заңдарын пайдаланып есептеу тәсілі; 2) Контурлық токтар тәсілі; 3) Түйіндік потенциалдар тәсілі; 4) Екі түйіндік тәсіл; 5) Балама генератор тәсілі.

Кирхофтың заңдарын пайдалану арқылы есептеу тізбектің тармақтарындағы анықталуға тиісті токтарға қатысты теңдеулер құрудан басталады. Құрылатын теңдеулер саны белгісіз токтар санына тең. Кирхгофтың бірінші заңы бойынша құрылатын теңдеулер саны тізбектегі түйін санынан біреуге кем болады, яғни т-1 тең. Мұндағы т- тізбектегі түйіндер саны. Кирхгофтың екінші заңы бойынша құрылатын теңдеулер саны жалпы құрылатын теңдеулер саны мен бірінші заңы бойынша құрылатын теңдеулер санының айырмасына тең, яғни к -( т-1). Мұндағы к-тізбектегі тармақтар саны. Кирхгофтың екінші заңы бойынша теңдеулер құру кезінде басқа контурға кірмеген тармағы бар тәуелсіз контурлар үшін құруға тырысқан жөн.

Кирхгофтың заңдары бойынша

6-суретте көрсетілген тізбек үшін теңдеулер құру:

Түйіндер үшін

а) –I₁– I₆ – I₃ =0

б) I₁+I₂ – I₅ =0

в) I₆ – I₂ – I₄ =0

Контурлар үшін

1-контур) E₁ – E₃=I₁∙R₁+I₅∙R₅ – I₃∙R₃

2-контур) –E₂+E₄= -I₂∙R₂+I₄∙R₄ – I₅∙R₅

3-контур) E₃ – E₄= –I₆∙R₆–I₄∙R₄ + I₃∙R₃

Теңдеулер жүйесін өзімізге белгілі әдестер арқылы шешеміз де, I₁,I₂,I₃,I₄,I₅,I₆ токтарды табамыз

6-сурет

2.Контурлық токтар тәсілі. Бұл тәсілді қолданған кезде электр сұлбасының тәуелсіз контурында тек өзінің контурлық тогы жүреді деп есептейді. Контурлық ток деп қарастырылған контурдың барлық тармақтарымен жүреді деп шартты түрде қабылданған ток. Бұл тәсіл бойынша теңдеулер Кирхгофтың екінші заңы бойынша контурлық токтарға байланысты құрылады. Сондықтан есептеу жұмысы көп жеңілдейді.

Контурлық токтар тәсілінің есептеу жұмысында қолданылуын 6-суретте көрсетілген тізбектің тармақтарындағы токтарды анықтау арқылы қарастырайық. Әрбір контур үшін контурлық токтың бағытын өз қалауымызша, мысалы сағат тілінің жүрісінің бағытымен бағыттас етіп таңдап аламыз. Екі контурға ортақ тармақпен жүретін контурлық токтар бағыттас болса, онда олардың қосындысы алынады. Керісінше жағдайда олардың айырмасын алады. Жалпы жағдайда қарастыралатын тізбек үшін теңдеулер мынадай түрде жазылады:

Е ₁₁= I₁₁∙R₁₁+ I₂₂∙R ₁₂ + I ₃₃∙ R ₁₃

Е₂₂= I₁₁∙R₂₁+ I₂₂∙R ₂₂ + I ₃₃∙ R ₂₃

Е₃₃= I₁₁∙R₃₁+ I₂₂∙R ₃₂ + I ₃₃∙ R ₃₃

Мұндағы Е₁₁, Е₂₂, Е₃₃- бірінші, екінші және үшінші контурлардың контурлық э.қ.к.-тері;

R₁₁, R₂₂, R ₃₃- бірінші, екінші және үшінші контурлардың өзіндік кедергілері,

R₁₁= R₁+R₅ +R₃; R₂₂= R₂+R₄+R₅; R ₃₃= R₆+R₄ +R₃.

R ₁₂=R₂₁- бірінші мен екінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

R₁₃= R₃₁- бірінші мен үшінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

R ₂₃= R ₃₂- екінші мен үшінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

Теңдеулер 6-суретте көрсетілген тізбек үшін былай жазылады:

E₁ – E₃=I₁₁∙(R₁+R₅ +R₃) – I₂₂∙R₅ –I₃₃∙R₃

– E₂+E₄= I₂₂∙ (R₂+R₄+R₅) – I₃₃∙R₄ –I₁₁∙R₅

E₃ – E₄=I₃₃∙ (R₆+R₄ +R₃) – I₁₁∙R₃– I₂₂∙R₄

Әр теңдеудегі жақшаның ішінде кедергілердің қосындысы контурдың өзіндік кедергісі деп аталады. Теңдеулер жүйесін шешеміз де I_11, I_22, I₃₃ контурлық токтарын табамыз. Тармақтардың токтарын (I₁ ... I₆) контурлық токтар арқылы табамыз:I₁=I₁₁, I₂= –I ₂₂, I₃= I₃₃ – I₁₁, I₄=I₂₂–I₃₃, I₅=I₁₁ – I₂₂, I₆= –I₃₃

3.Түйіндік потенциалдар тәсілі. Сұлбалардағы түйіндердің потенциалдарын белгісіз ретінде қабылдап, электр тізбектерін есептеу тәсілін түйіндік потенциалдар тәсілі деп атайды.Айталық, сұлбада n-түйін болсын. Сұлбаның кез-келген бір нүктесін ойша жермен қосамыз, яғни оның потенциалын нөлге тең деп аламыз.Соның нәтижесінде белгісіздер саны n-1-ге дейін азаяды. Бұл тәсіл бойынша теңдеулер Кирхгофтың бірінші заңы бойынша түйінде түйіскен токтарға арнап құрылады. Токтарды түйіндердің потенциалдары арқылы Ом заңы бойынша өрнектеуге болады. Нәтижесінде теңдеулер жүйесі мынадай түрде жазылады:

φ ₁G₁₁ + φ₂G₁₂ + φ₃G₁₃= I₁₁

φ₁G₂₁ + φ₂G₂₂ + φ₃G₂₃= I₂₂

φ₁G₃₁ + φ₂G₃₂ + φ₃G₃₃= I₃₃

φ₁, φ₂, φ₃- бірінші, екінші және үшінші түйіндердің потенциалдары; G₁₁, G₂₂, G₃₃-- бірінші, екінші және үшінші түйіндерде түйіскен тармақтардың өткізгіштердің қосындысы; G_km- k мен m түйіндерді байланыстыратын тармақтың өткізгіштігі, “минус” таңбасымен алынады; I₁₁, I₂₂, I₃₃- түйіндердің түйіндік токтары. Белгілі бір түйіннің түйіндік тогы сол түйінмен байланысқан тармақтардағы э.қ.к.-терді сол тармақтардың кедергілеріне бөлу арқылы табылған токтардың алгебралық қосындысына тең. Э.қ.к.-тері түйінге бағытталған тармақтардың токтары «плюс» таңбасымен алынады, ал керісінше жағдайда «минус»таңбасы алынады.

Берілген тізбектің (6-сурет) « г» түйінінің потенциалын нөлге тең деп аламыз.Теңдеулер көрсетілген тізбек үшін былай жазылады:

φ _а(g₁+g₃+g₆) - φ_бg₁ - φ_вg₆= -E₁g₁-Е₃g₃

φ_б(g₁+g₂+g₅) - φ_аg₁ - φ_вg₂= E₁g₁ + E₂g₂

φ_в(g₂+g₄+g₆) - φ_бg₂ - φ_аg₆= -E₂g₂ -E₄g₄

Мұндағы g₁=1/R ₁, g₂=1/R₂, g₃=1/R₃ , g₄=1/R₄ , g₅=1/R₅ , g₆=1/R₆.

Теңдеулер жүйесін шешу арқылы φ_а, φ_б, φ_в табамыз. Токтардың мәндерін Ом заңы арқылы табамыз:

I₁= (E₁+ U_аб)/R₁ = [E₁+(φ_а - φ_б)]/R₁, I₂= (E₂+ U_вб)/R₂=[E₂+(φ_в- φ_б) ]/R₂, I₃= (E₃+ U_аг)/R₃=[E₃+ (φ_а - φ_г) ]/R₂

I₄= U_вг/R₄=(φ_в - φ_г)/R₄ = φ_в/R₄ I₅= U_бг/R₅=(φ_б - φ_г)/R₄ = φ_б/R₅ I₆= (E₆+ U_ав)/R₆=[ E₆+ (φ_а - φ_в) ]/R₆

Негізгі әдебиеттер: [1(24-33, 35-40), 3(68-71, 74-80, 98-103)]

Қосымша әдебиеттер: [ 4,5,7,8]

Бақылау сұрақтары:

1.Бірнеше э.қ.к-ілері бар күрделі тұрақты ток тізбектерін есептеу тәсілдері. Ом және Кирхгоф заңдарын пайдалану арқылы есептеу.

2.Контурлық токтар тәсілі.

3.Түйіндік потенциалдар тәсілі.

№4 Дәріс. Екі түйіндік тәсіл. Екіұштықтар. Балама генератор тәсілі. Энергияны активті екіұштықтан пассивті екіұштыққа беру

Е кі түйіндік тәсіл. Көп жағдайда екі түйіннен тұратын электр сұлбалар кездеседі. Мұндай сұлбаларды есептеу үшін түйіндік потенциалдар тәсілінің жеке бір түрі –екі түйіндік тәсілді қолданған тиімді. Бұл тәсіл бойынша екі түйін арасындағы кернеуді табу арқылы тармақтардағы токтарды анықтайды. Мысалы, 7-суреттегі тізбектің тармақтарындағы токтарды табайық. Ол үшін алдымен U_аб кернеуін табамыз. Тізбектің «б » түйінінің потенциалын нөлге тең деп аламыз. Сонда U_аб=φ_а – φ_б = φ_а – 0 = φ_а.

Тізбектің «а » түйіні үшін: I₁ + I₂ +I₃ + I₄=0,

мұндағы I₁= (E₁ - U_аб)/R₁=(E₁-φ_а)/R₁,

I₂= - U_аб . R₂= -φ_а . R₂, I₃= (-E₃ - U_аб).R ₃=(-E₃-φ_а).R₃, I₄= -φ_а . R₄.

Токтардың өрнектерін теңдеуге қоямыз да , φ_а табамыз:

φ_а(g₁+g₂+g₃+g₄)= E₁g₁ – E₃g₃,

φ_а=(E₁g₁ – E₃g₆)/ (g₁+g₂+g₃+g₄).

Табылған φ_а мәнін токтардың өрнектеріне қойып, олардың мәндерін анықтаймыз. Табылған φ_а мәнін токтардың өрнектеріне қойып, олардың мәндерін анықтаймыз. Жалпы жағдайда U_аб =∑ E_кg_к /∑g_к.

Балама генератор тәсілі. Бұл тәсіл күрделі тізбектің бір тармағындағы токты табу үшін қолданылады. Бұл тәсіл бойынша есептеу үшін қарастырылатын тармақты тізбектің басқа бөлігінен бөліктеп аламыз. Қалған бөлікті активті екіұштық деп қарастырамыз. Активті екіұштық дегеніміз екі ғана жалғану ұшы бар, ал ішінде э.қ.к. мен резисторлар бар тізбекті айтамыз (8-сурет).

8-сурет

Егер екіұштықтың ішінде энергия көзі (қоректендіргіш) болмаса, онда оны пассивты екіұштық дейді және оны электр энергиясын қабылдаушы деп санайды. Балама сұлбада пассивты екіұштықты бір кедергімен бейнелейді. Ол кедергіні екіұштықтың ішкі немесе кірістік кедергісі деп атайды.

Тізбектің бөлектенген тармағына байланысты активті екіұштықтықты балама генератормен айырбастауға болады. Бұл генератордың э.қ.к.-і E_б бос жүріс режимі кезінде бөлектенген тармақтың қысқыштарындағы кернеуге U_бж тең, ал _, ішкі кедергісі R_б екіұштықтықтың кірістік кедергісі R_i тең.

Қарастырылатын тармақтағы токты табуды мынадай ретпен жүргізген жөн:

а)E_б-ні табу үшін бос жүріс режимін қарастырамыз, яғни тогы анықталуға тиісті тармақты а және б нүктелерінде үзіп, екіұштыдан оны айырып тастаймыз. Онан кейін а және б нүктелерінің арасындағы кернеуді U_аббж есептік жолмен немесе өлшеу арқылы табамыз.

ә) Генератордың ішкі кедергісі R_б табу үшін а және б нүктелеріне байланысты екіұштықтың толық кедергісін анықтаймыз. Ол үшін екіұштықтың сұлбасындағы э.қ.к.-терді алып тастап, олардың орындарын қысқы тұйықтаймыз. Сұлбада тек кедергілерді қалдырамыз.

б) Қарастырылатын тармақтағы токты мына формула бойынша табамыз: I= U_аббж /( R_ж+ R_i) .

Егер қарастырылатын тармақтың кедергісін нөлге теңестірсе ( R_ж =0), онда ол үшін қысқаша тұйықталу режимі орын алады. Тармақпен қысқаша тұйықталу тогы (I_қ.т) жүреді: I_қ.т= U_аббж /R_і. Бұдан

R_і .=U_аббж /I_қ.т , яғни ішкі кедергіні табу үшін бос жүріс режимі кезінде өлшенген кернеуді U_аббж қысқаша тұйықталу режимі кезінде өлшенген токқа I_қ.т бөлу керек.

Энергияны активтік екіұштықтан жүктемеге беру. Активті екіұштыққа қосылған жүктемеде R_ж бөлінетін қуат P = I² R = U_аббж R_ж /( R_ж+ R_i). Қабылдағышқа максимал қуат беру шартын анықтау үшін P-ның R_ж бойынша бірінші ретті туындысын тауып,оны нөлге теңейміз. Осыдан R_ж = R_i. Демек осы теңдік орындалған жағдайда жүктемеде максимал қуат бөлінеді: P_max= U²_аббж /4R_і. Балама генераторда бөлінетін толық қуат P_тол =U_аббж I =U²_аббж /( R_ж+ R_i). Пайдалы әсер коэффициенті ( п.ә.к.): η= P/ P_тол = R_ж /( R_ж+ R_i). Егер R_ж = R_i болса, онда η=0,5.

Активті екіұштықтың кірістік кедергісіне R_i тең жұктеме кедергіні R_ж келістіру немесе үйлестіру жүктемесі деп атайды.

Б айланыс жүйелерінде, электроникада көп жағдайда қабылдағышқа максимал қуат берудің маңызы зор.

Беріліс желісі арқылы энергияны тасымалдау. Электр желісінің сұлбасы 9а-суретте бейнеленген, мұндағы U₁ –желінің басындағы генератордың кернеуі; U₂ – желінің соңындағы жүктеменің кернеуі; R_с –желінің сымдарының кедергісі; R_ж – жүктеменің кедергісі.

Нақты желілер арқылы үлкен қуат бергенде η = 0,94...0,99 болса онда U₂ кернеуі U₁ – ден бірнеше пайызға кіші болады. Өте үлкен қуатты алыс қашықтыққа тасымалдағанда п.ә.к.- тің жоғары болуы экономикалық жағынан тиімді. Желінің басындағы қуаттың P₁ және жүктемедегі қуаттың P₂ , п.ә.к пен U₂ –нің жүктемедегі токта тәуелді өзгерістерін сипаттайтын сызықтар 9ә-суретте бейнеленген. Олар төмендегі теңдеулер негізінде салынған: P₁=U₁I; P₂=U₁I- I² R_с; η = R_ж /( R_ж+ R_с); U₂=U₁ - I R_с. Токтың максималдық мәні I_max = U₁ / R_с жүктеменің қысқаша тұйықталу кезінде орын алады.

Желінің п.ә.к.-інің мәні U₁ кернеуі неғұрлым жоғары болған сайын, соғұрлым жоғары болады.

Негізгі әдебиеттер: [1(40-41, 54-58), 3(97-98, 109-118)]

Қосымша әдебиеттер: [ 4,5,7,8]

Бақылау сұрақтары:

1.Қандай тізбектерді есептеу үшін екі түйіндік тәсіл қолданылады? Бұл тәсіл бойынша тізбекті есептеу қалай жүргізіледі?

2.Қандай жағдайда тізбекті есептеу үшін балама генератор тәсілін қолданады? Бұл тәсіл бойынша тізбекті 9-сурет есептеу қалай жүргізіледі?

3.Энергияны активті екіұштыдан пассивті екі ұштыға беру. Қабылдағышқа максимал қуат беру шарты қандай? Пайдалы әсер коэффициенті ( п.ә.к.) қалай анықталады?

4.Энергияны беріліс желісі арқылы тасымалдаған кезде жүктемедегі кернеудің, жүктемеде бөлінетін қуаттың және п.ә.к.-тің токқа тәуелді өзгерістерінің сипаты қандай?

№5 Дәріс. Синусоидалы ток тізбегі. Синусоидалы шамаларды сипаттайтын параметрлер. Синусоидалы шамалардың мәндері және оларды бейнелеу жолдары

Синусоидалы ток практикада кеңінен қолданылады. Синусоидалы токтың тұрақты токқа қарағанда мынадай артықшылықтары бар: а) Синусоидалы ток өндіретін қондырғылардың (генераторлардың) құрылысы тұрақты ток генераторларына қарағанда қарапайым, жұмыс істеу сенімділігі өте жоғары және бағасы арзан; ә) Трансформаторларды қолдану арқылы синусоидалы кернеудің мәнін өте жоғары дәрежеге көтеруге болатындықтан синусоидалы токты алыс қашықтыққа жеткізу арзанға түседі; б)Синусоидалы токты пайдаланып жұмыс жасайтын электр қондырғылардың құрылысы тұрақты ток қондырғыларына қарағанда әлде қайда қарапайым және арзан.

Синусоидалы ток деп мәні уақытқа тәуелді синусоидалық заңдылықпен өзгеретін токты айтамыз: i=I_m*sin( t+ ). Оның графигі 10-суретте көрсетілген. Синусоидалы токты мынадай параметрлер арқылы сипаттауға болады:

1)Амплитудалық мән ( I_m, U_m, E_m ) – синусоидалық шаманың ең үлкен максимал мәні.

2)Периоды ( Т ) – толық бір тербеліс жасауға кететін уақыт.[c]

3)Жиілік ( f ) – бір секунда ішінде жасалатын тербеліс саны.[1/c];[Гц] f=1/T; T=1/f

4 )Бұрыштық жиілік (ω) ω =2πf= 2π/ T, [рад/с]

5)Фаза ( t+ φ ) – кез келген сәттегі синусоидалық шаманың мәнін анықтауға мүмкіндік береді.

6)Бастапқы фаза φ - синусоидалық шаманың уақыт нөлге тең болған кездегі мәнін анықтауға мүмкіндік береді. Егер φ таңбасы оң болса, онда синусоида ордината осі бойынша солға қарай φ бұрышқа ығысады. ,

ТМД елдерінде және Еуропаның біраз елдерінде жиілігі 50Гц синусоидалы кернеу кеңінен қолданылады.

10-сурет Синусоидалы шамалардың мәндері: а) Амплитудалық мән ( Im, Um, Em ); ә) Лездік мән ( i, u, e ) - синусоидалы шаманың кез келген сәттегі мәні: i=Imsin( t+ _i); u=U_msin( t+ _u); e=E_msin( t+ _e); б) Орташа мән (I_ор, U_ор, E_ор) - синусоидалы шаманың жарты период ішіндегі орташа мәні:

I_ор= = = I_m=o.638I_m: U_ор= = U_m=0.638U_m.

Сонымен орташа мән амплитудалық мәннен π/2 есе аз.

в)Әрекеттік мән ( I, U, E ) немесе орташа квадраттық мән

I= = = I_m/ =0.707I_m, сол сияқты U= U_m/ = 0.707U_m, Е=0.707E_m.

Синусоидалы шамалардың әрекеттік мәндері олардың амплитудалық мәндерінен есе аз. Синусоидалы ток әрекеттік мәні кедергі арқылы жүрген кезде бір период ішінде синусоидалы ток қанша жылу бөлсе, сонша уақытта сондай жылу бөліп шығаратын тұрақты токтың мәніне тең.

Өлшеу аспаптардың көпшілігі синусоидалы шаманың әрекеттік мәнін көрсетеді.

Синусоидалы шамаларды бейнелеу жолдары: а) Тригонометриялық функциялар арқылы бейнелеу: i=I_msin( t+ _i) ; u=U_msin( t+ _u);

ә) Тікбұрыштық координаталарда уақыттық диаграмма арқылы бейнелеу ( 10-сурет);

б ) Айнымалы вектор арқылы бейнелеу. Тікбұрыштық координаталар жазығында ұзындығы синусоидалы токтың i=I_msin( t+ ) амплитудасына I_m тең вектор тең бұрыштық жылдамдықпен айналып тұр делік (11-сурет). Бастапқы жағдайда вектор абцисса осінен бұрышына ығысқан. Уақыт өткен сайын вектор t жылдамдығымен айналып, шеңбер сызып шығады Егер вектордың әрбір сәттегі ордината осіндегі проекциясыларын уақыттық диаграмма түрінде бейнелесек, онда проекцияның синусоидалы заңдылықпен өзгеретіндігін көреміз, яғни вектордың ордината осіндегі проекциясының уақытқа тәуелді өзгерісі синусоидалы шаманың лездік мәндерін өзгерісін сипаттайды. Демек, синусоидалы шаманы ұзындығы оның амплитудасына тең, жылдамдығы оның бұрыштық жиілігіне тең айналмалы вектор түрінде бейнелеуге болады. Вектордың бастапқы жағдайы синусоидалы шаманың бастапқы фазасымен анықталады. Бұрыштық жиілігі бірдей бірнеше синусоидалы шамалардың векторлары бірдей жылдамдықпен айналады. Сондықтан олардың өзара орналасуы өзгермейді. Сол себепті практикада оларды айналдырмайды, оларды бастапқы фазаларына сәйкес жазықтықта өзара орналастырады. Векторларды айналдыру қажеттігі болмағандықтан координаталар осьтерін көрсетудің қажеті болмайды. Бірінші векторды горизонталь немесе вертикал орналастырады да, қалғандарын бастапқы фазаларына сәйкес осы векторға байланысты орналастырады.

Синусоидалы шамалардың векторларлар түрінде бейнелеу оларды геометриялық жолмен қосу немесе алу операциясын орындауға мүмкіндік береді.

в) Синусоидалық шамаларды комплекс сандар арқылы бейнелеу. Синусоидалы шама тригонометиялық функция түрінде берілсін: i=I_msin( t + φ). Комплекстік жазықтыққа ұзындығы амплитудаға I_m тең, ал нақты осьпен құрайтын бұрышы бастапқы фазаға φ тең вектор саламыз (12- сурет). Бұл вектордың ұшы белгілі бір комплекс санға - синусоидалы шаманың комплекстік амплитудасына сәйкес келеді. I_m = I_me^j - комплекстік амплитуда.Уақыт өткен сайын фаза өседі де, бұл вектор айналмалы векторға айналады: I_me^{j( t+ )}= I_mcos( t+ )+ jI_msin( t+ ). Жорамал бөлік синусоидалы шамаға тең, яғни синусоидалы шаманы комплекс санның жорамал бөлігі арқылы көрсетуге болады.

Синусоидалы шамаларды комплекстік жазықтықта векторлар арқылы көрсету оларды қосып, алуға (геометриялық жолмен) мүмкіндік береді.

Векторлық диаграмма деп жиіліктері бірдей синусоидалық шамаларды комплекстік жазықтықта олардың бастапқы фазаларына сәйкес өзара орналасқан векторларының жиынтығын айтады. Фазалық ығысу деп синусоидалық шамалардың бастапқы фазаларының айырмасын айтады: =φ₂ - φ₁.

Негізгі әдебиеттер: [1(59-72), 3(136-145)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1.Синусоидалы ток деп қандай токты атайды?. Синусоидалы шамаларды сипаттайтын қандай параметрлерді білесіз?

2.Синусоидалы шамалардың қандай мәндері бар? Олар қалай анықталады?

3. Синусоидалы шамаларды тікбұрыштық координаталарда уақыттық диаграмма арқылы бейнелеуге түсініктеме беріңіз.

4. Синусоидалы шамаларды айнымалы вектор арқылы бейнелеуге түсініктеме беріңіз.

5. Синусоидалық шамаларды комплекс сандар арқылы бейнелеуге түсініктеме беріңіз.

№6 Дәріс. Активті кедергісі бар тізбек. Идеал индуктивті элементі бар тізбек. Идеал сыйымдылық элементі бар тізбек

Активті кедергісі бар тізбек. Кедергісі бар элементті резистор дейді. Осы резистордың айнымалы токқа көрсететін кедергісін активті кедергі деп атайды. Активті кедергі айнымалы токтың электр энергиясының жылу энергиясына айналуын сипаттайды.

13-сурет	Синусоидалы кернеуді u=Umsin( t+ u) активті кедергісі бар тізбекке берсек ( 13а-сурет) , онда кедергі арқылы жүретін токтың лездік мәні i=u/r= Um/r sin( t+ u)=Imsin( t+ i). Бұдан токтың әрекеттік мәні I= (Um/ ) /r, ал фазасы i= u, Фазалық ығысу = u- i = 0 Сонымен токтың I және кернеудің комплекстердің U векторлары өзара бір түзудің бойында орналасады және бағыттас болады ( 13б-сурет). Лездік қуат деп кернеудің лездік мәнінің токтың лездік мәніне көбейтіндісін айтады: р=ui = UmImsin2 t = UmIm( )=
14-сурет		Лездік қуат тұрақты құраушыдан және екі еселенген жиілікпен өзгеретін айнымалы құраушыдан тұрады ( 14-сурет). Оның таңбасы әр уақытта оң, яғни электр энергиясы тұрақты түрде басқа түрлі энергияға түрленеді. Период ішіндегі орташа қуатты активті қуат деп атаймыз: P= , немесе P=UI= =I2 r = . Активті қуаттың өлшем бірлігі ретінде Ватт ( Вт) қабылданған. Идеал индуктивті элементі бар тізбек (15-сурет). Индуктивтік элемент уақытқа байланысты магнит ағынының өзгерісінен э.қ.к.-тің туу құбылысын және нақты электр тізбегінің элементінде магнит өрісінің

энергиясының жинақталу құбылысын есептеуге мүмкіндік береді. Индуктивті орамамен айнымалы ток жүрген кезде оның бойында бағыты сол токқа қарама- қарсы өзіндік э.қ.к. e_L пайда болады.

15-сурет 16-сурет 17-сурет

Оны берілген кернеу теңгереді: u = -eL, мұндағы eL= - L . Бұдан uL= L . Егер ток синусоидалы болса i=Imsin t, онда uL = L = Im Lcos t = Umsin( t+90o), мұндағы Um=Im* L=Im xL, ал xL= L индуктивті кедергі деп аталады. Фазалық ығысу = u - i =90o , яғни векторлық диаграммада кернеудің U векторы токтың I векторы фаза бойынша 90о-қа озады(16-сурет). Лездік қуат: p = iu = Im sin t Umcos t = (sin2ωt) UmIm/2, яғни оның екі еселенген жиілікпен өзгеретіндігін көреміз. Оның амплитудасын QL реактивті индуктивті қуат деп атайды. QL= ; Өлшем бірлігі - вольтампер реактивтік [ВАр]. Периодтың бірінші ширегінде индуктивті элемент электр желісінен энергия алып, оны магнит өрісінің энергиясына айналдырады да, бойына жинайды(17-сурет). Екінші ширекте лездік қуаттың таңбасы теріс, яғни индуктивті элемент бойына жинақтаған магнит энергиясын электр энергиясына түрлендіріп, электр желісіне қайтарады. Үшінші ширекте индуктивті элемент электр желісінен энергия алады да,

төртінші ширекте сол энергияны қайтарады. Период ішіндегі орташа қуат нөлге тең( P=0). Сонымен индуктивті элементте электр энергиясының магнит энергиясына, магнит энергиясының электр энергиясына айналу құбылысы алма кезек жүріп жатады.

Идеал сыйымдылық элементі бар тізбек ( 18-сурет). Егер сыйымдылық элементке синусоидалы кернеу u = U_msin t берілген болса, ондағы заряд та синусоидалы заңдылықпен өзгереді:

18-сурет 19-сурет

q=Cu= СUmsin t. Сыйымдылық элементпен жүретін ток i = dq/dt = C . Бұдан Im= UmC = = Um/xc , мұндағы xC= сыйымдылық кедергі. Токтың әрекеттік мәні I= Uc/xc. Фазалық ығысу = u - i =0-90o= -90o, яғни векторлық диаграммада сыйымдылық элементпен жүретін токтың I векторы кернеудің U векторынан фаза бойынша 90о-қа озады (19-сурет). Лездік қуат: p = i u = Imsin( t+90o)Umsin t = (sin2 t) , яғни ол екі еселенген жиілікпен өзгереді Оның амплитудасын реактивті сыйымдылық қуат Qс деп атайды. QC= ; Өлшем бірлігі- [ВАр]

Конденсатор периодтың бірінші және үшінші ширектерде қоректендіргіштен энергия алып, бойына жинайды( яғни зарядталады ). Ал екінші және төртінші ширектерде бойына жинаған энергияны электр желісіне қайтарып береді (17-сурет) . Сонымен конденсаторда энергия алмасу құбылыстары жүріп жатады. Период ішіндегі орташа қуат, яғни активті қуат нөлге тең (Р= 0).

Негізгі әдебиеттер: [1(72-78, 94-98), 2(145-152)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1. Активті кедергісі бар тізбек үшін ток және фазалық ығысу қалай анықталады? Бұл тізбек үшін векторлық диаграмма тұрғызыңыз. Тізбектің лездік қуатын аналитикалық және графикалық жолмен сипаттаңыз. Активті қуат неге тең?

2.Идеал индуктивті элементі бар тізбек үшін кернеуді, индуктивті кедергіні және фазалық ығысуды қалай анықталады? Векторлық диаграммада кернеу мен токтың векторларының өзара орналасуына түсініктеме беріңіз.Лездік қуаттың сипаты қандай? Индуктивті реактивті қуат қалай анықталады?

3. Идеал сиымдылық элемент бар тізбек үшін ток, сиымдылық кедергі және фазалық ығысу қалай анықталады? Бұл тізбек үшін векторлық диаграмма тұрғызыңыз. Тізбектің лездік қуатын аналитикалық және графикалық жолмен сипаттаңыз. Сыйымдылық реактивті қуат неге тең?

№7 Дәріс. Активті кедергісі, идеал индуктивті элемент және сыйымдылық элементтер бірізді жалғанған тізбек

Бірізді жалғанған r, L және C элементтерден тұратын электр тізбегі арқылы ( 20-сурет) синусоидалы ток i=I_msin t жүргенде, осы тізбектегі кернеулердің лездік мәндері үшін Кирхгофтың екінші заңы бойынша теңдеу құруға болады: u= u_r+u_L+u_C. Онда тізбек күйінің теңдеуі:

20-сурет

u= ri+ L + = rImsin t+Im Lcos t - немесе u=rImsin t+Im Lsin( t+90o)+ =Umrsin t+UmLsin( t++90o) +Umcsin( t - 90o). Уақытқа тәуелді үш синусоидалы функцияның қосындысын комплекстік тәсілмен есептеген тиімді. Лездік кернеу мен ток негізінде комплекстік ток пен кернеуді жазайық: I ,

U_r I, U_L I , U_C= I , U= , j=e^j90˚ , -j=e ^--j90˚

Комплекстік кернеулер мен токты векторлық диаграммада көрсетейік. Фаза бойынша U_r кернеу I токпен дәл келеді, U_L фаза бойынша I токтан 90^o алға озады, ал U_C кернеуі фаза бойынша I токтан 90^o

21-сурет 22-сурет 23-сурет

кеш қалады (17-сурет). Ur, UL, және UC векторларды қосу нәтижесінде U векторын аламыз. Бұл векторлар кернеулер үшбұрышын құрайды (21-сурет). Оның бір катетін активті кернеу Ur, екінші катеті реактивті кернеу Up= UL – UC , ал гипотенузаны толық кернеу U құрайды. Пифагор теоремасы бойынша: U= = = = =Iz, мұндағы z - толық кедергі. U кернеуінің векторымен I ток векторының арасындағы бұрыш - фазалық ығысуды φ анықтайды: φ= arctg . Егер UL<UC болса, онда φ таңбасы теріс болады. Кернеулер үшбұрышынан активті кернеуді Ua және реактивті кернеуді Up толық кернеу U мен фазалық ығысу φ арқылы табуға болады: Ua= Ur= Ucos φ ; Up= Usin φ. Тізбектің толық кедергісінің z формуласындағы xL – xC айырмасын реактивті кедергі xp деп атайды, яғни xp= xL – xC.. Толық кедергінің өрнегі бір катеті активті кедергіге r, екінші катеті реактивті кедергіге xp, ал гипотенузасы толық кедергіге z тең тікбұрышты үшбұрышқа сәйкес келеді. Бұл үшбұрышты кедергілер үшбұрышы деп атайды (22-сурет). Бұл үшбұрыштан фазалық ығысу φ= arctg xp / r. Оның таңбасы xL < xC болғанда теріс болады. Егер z және φ белгілі болса, онда кедергілер үшбұрышынан r = z cos φ ; xp= z sin φ.

Лездік қуат: p= ui= -

= , мұндағы p_a= -активті лездік қуат; ал p_p= - реактивті лездік қуат;

Активті лездік қуат p_a=U_aI – U_aIcos2 t= UIcos - UIcos cos2 t, яғни ол тұрақты құраушыдан және айнымалы құраушыдан тұрады. Айнымалы құраушы екі еселенген жиілікпен өзгеретін, амлитудасы UIcos -ге тең косинусоида болады. Лездік қуаттың бір период ішіндегі орташа мәні активті қуат деп аталады. Ол лездік қуаттың тұрақты құраушысына тең: P= UI cos = u_aI= rI².

Индуктивті лездік қуат: p_L= , сиымдылық лездік қуат: p_C= . Бұл қуаттардың фазалары қарама-қарсы. Тізбектің реактивті қуаты:

p_p= p_L+p_C=( x_L – x_C) I² sin2 t = x_p I² sin2 t = U_p I sin2 t= UI sinφsin2 t.

Лездік қуат: p= UIcos - UIcos cos2 t + UIsin sin2 t = UIcos + UIsin(2 t+ - 90^o), яғни

24-сурет

ол тұрақты құраушыдан және айнымалы құраушыдан тұрады (24-сурет). Айнымалы құраушының амплитудасы UI тұрақты құраушыдан артық болғандықтан лездік қуат кейбір сәттерде теріс таңбалы болады. Бұл кезде тізбек қоректендіргішке энергияны қайтып береді. Қайтарылатын энергия тізбектің реактивті бөлігінің энергиясының есебінен жүреді. Айнымалы бөліктің амплитудасын S деп белгілейміз де, толық қуат деп атаймыз: S= IU. Өлшем бірлігі- вольтампер [ВА]. Лездік реактивті қуаттың амплитудасын (UIsin ) реактивті қуат Qp= UIsin деп атайды. Өлшем бірлігі- вольтампер реактивтік [ВАр]. Qp= QL – QC= xLI2 – xCI2= ULI – UC I =Up I.

Кедергілер үшбұрышының қабырғаларын I² көбейтсек, онда қуаттар үшбұрышын аламыз. Оның бір катеті активті қуатқа P, екінші катеті реактивті қуатқа Q_p , ал гипотенузасы толық қуатқа S сәйкес келеді. Бұл үшбұрыштан толық қуат:S= , φ= arctg Q_p/ P, немесе P= Scos , Q_p = Ssin .

Әр түрлі электротехникалық қондырғыларда бір мезгілде электр энергиясының жылулық немесе механикалық энергияға айналуының қайтымсыз процестерімен қатар қайтымды процесс- электр энергиясының магнит энергиясына айналуы жүріп жатады. Активті қуат пайдалы жылуға немесе механикалық жұмысқа жұмсалатын болғандықтан электр энергиясының бір бөлігі ғана жұмсалады. Реактивті қуат пайдалы жұмыс жасамайды.

Активті қуаттың толық қуатқа қатынасын электротехникада қуат коэффициенті деп атайды: cos = P/ S.

Негізгі әдебиеттер: [1(78-86, 94-98), 3( 152-156, 190-196)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1. Бірізді жалғанған r, L және C элементтерден тұратын электр тізбек күйінің теңдеуіне түсініктеме беріңіз.

2.Векторлық диаграммада токтың және кернеулердің векторларының өзара орналасуы. Кернеулер үшбұрышы. Активті, реактивті және толық кернеулер.

3. Кедергілер үшбұрышы. Тізбектің активті, реактивті және толық кедергілері.

4. Тізбектің лездік қуаты. Активті, реактивті және толық қуат.

5. Қуаттар үшбұрышы. Қуат коэффициенті.

№8 Дәріс. Активті кедергі, идеал индуктивті элемент және сыйымдылық элементтер параллель жалғанған тізбек

П араллель қосылған активті кедергі r, идеал индуктивті элемент L және сыйымдылық элементтен C тұратын электр тізбегін синусоидалы кернеуге u=U_msinωt қосайық(25-сурет). Барлық тармақтардағы токтарды анықтайық. Кирхгофтың бірінші заңы бойынша:

, немесе i=(U_m/r)sinωt+(U_m/ωL) sin(ωt-90˚)+ωCU_m sin(ωt+90˚).

Комплекстік әрекеттік мәндерге көшейік:

I =Ie^jφ, I_a= I_ae^j0, I_L=I_Le^-j90˚ , I_C=I_Ce^j90˚ , мұндағы I_a=U/r, I_L=U/ωL,

I_C=UωC – токтардың модульдері, ал U=U_m/ . Алынған теңдеуден активті кедергідегі токтың фаза бойынша кернеумен бірдей болатынын көреміз. Ток индуктивті элементте фаза бойынша 90˚ артта қалады, ал ток сыйымдылық элементтегі кернеуден фаза бойынша 90˚ озады. Кернеу мен токтардың векторларының өзара орналасуы 26-суреттегі векторлық диаграммада көрсетілген. Индуктивті ток I_L пен сыйымдылық токтың I_C фазалары қарама-қарсы болғандықтан олар бір бірінен алынады. Олардың айырымын реактивті ток деп атайды: I_p= I_L- I_C. Векторлық диаграммадан активті ток I_a, реактивті ток I_p және тізбектің толық тогы I тікбұрышты үшбұрыш құрайтынын көреміз. Бұл токтар үшбұрышының катеттерін I_a және I_p токтары құрайды да, ал гипотенузасы I тогы болады. Пифагор теоремасы бойынша : , ,

мұндағы – тізбектің толық өткізгіштігі. Бұл өрнектегі g=1/r-активті өткізгіштік деп, b_L=1/x_L=1/ ωL реактивті индуктивті өткізгіштік деп, ал b_C=1/x_C=1/ ωC реактивті сыйымдылық өткізгіштік деп аталады.

Токтар үшбұрышынан тізбектегі кернеудің U толық токтан I фаза бойынша қаншалықты ығысқандығын табуға болады: . Егер b_L > b_C болса φ таңбасы оң, ал b_L < b_C болғанда таңбасы теріс болады.

Егер толық ток I және φ белгілі болса, онда I_a= Icosφ, I_p= Isinφ.

27-сурет

Тізбектің толық өткізгіштігінің өрнегі бір катеті активті өткізгіштікке g тең, екінші катеті реактивті өткізгіштікке тең b (b= bL - bC), ал гипотенузасы толық өткізгіштікке y тең тікбұрышты үшбұрышқа сәйкес келеді( 27-сурет). Бұл үшбұрышты өткізгіштер үшбұрышы деп аталады Ток пен кернеу арасындағы фазалық ығысуды өткізгіштер үшбұрышы арқылы табуға болады: φ=arctg( bL - bC)/g. Бұл өрнектен фазалық ығысу индуктивті және сиымдылық өткізгіштіктердің өзара қарым-қатынасына байланысты екендігі көрінеді.

Егер b >0 болса, онда реактивті өткізгіштік b индуктивті сипатта, ал b_L < 0 сыйымдылық сипатта болады. Егер b = 0 болса, онда тізбекте токтар резонансы болды.

Егер y және φ белгілі болса, онда g= ycos φ, b= ysin φ.

Токтарды да, қуаттарды да өткізгіштіктер арқылы есептеуге болады: активті ток I_a=Ug, реактивті индуктивті ток I_L=Ub_L,, реактивті сыйымдылық ток I_C= Ub_C , ал тізбектің реактивті тогы I_p= Ub, толық ток I=U y.

Тізбекте бөлінетін активті қуат P=U²g, реактивті индуктивті қуат Q_L=U² b_L,, реактивті сыйымдылық қуат Q_C= U² b_C,, толық қуат S= U² y.

Негізгі әдебиеттер: [1(86-91), 3(167-171)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1.Параллель қосылған активті кедергі r, идеал индуктивті элемент L және сыйымдылық элементтен C тұратын электр тізбек күйінің теңдеуі. Активті, реактивті және толық токтар.

2. Векторлық диаграмма. Токтар үшбұрышы.

3.Тізбектің активті, реактивті және толық өткізгіштіктері. Өткізгіштіктер үшбұрышы.

4.Фазалық ығысу. Тізбектегі энергетикалық үрдістер.Активті, реактивті және толық қуаттар.

№9 Дәріс. Синусоидалы ток тізбегін есептеудің комплекстік тәсілі.

К омплекстік тәсіл лездік мәндер үшін құрылатын дифференциалдық теңдеуден комплекстік мәндер үшін құрылатын алгебралық теңдеуге өткізуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде синусоидалық шамаларды комплекстік сандар ретінде көрсетеді:

А , мұндағы b/a.

Егер , онда . Егер , онда

К ез-келген векторды -ға көбейткенде, ол вектордың модулін өзгертпей 90^о-қа бұрады.,ал - -ға көбейткенде векторды - 90^о-қа бұрады ( 28-сурет). Комплекстік тәсілді пайдалану арқылы синусоидалы шамалардың лездік мәндерін анықтайтын дифференциалдық теңдеулерден комплекстік мәндер арқылы өрнектелген алгебралық теңдеулерге көшуге болады. Бұл есептеу жұмысын жеңілдетуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде токтың лездік мәнін (i) оның комплекстік амплитудалық мәніне ( I _m) айырбастаймыз, ал лездік активті кернеуді u_a=ir комплекстік активті кернеумен. I_m r, лездік индуктивті кернеуді u_L=L di/dt комплекстік индуктивті кернеумен I_m jωL , ал лездік сыйымдылық кернеуді u_C=(1/C) ∫idt комплекстік сыйымдылық кернеумен I_m(-j/ωC), лездік э.қ.к.-ті e комплекстік кернеумен E_m айырбастаймыз.

29-суретте көрсетілген тізбекке Кирхгофтың екінші заңы бойынша лездік мәндер үшін теңдеу құрайық: u_a+ u_L+ u_C= e, немесе

I_m r

Теңдеуді комплекстік түрде жазайық: I_m r + I_m jωL - I_m(j/ωC) = E_m, I_m [ r + j( ωL --1/ωC)] = E_m ,

бұдан I_m = E_m / [ r +j ( ωL --1/ωC)]= E_m /Z .

Бұл теңдеудің оң жағын да, сол жағын да √2 бөлсек, онда комплекстік әрекеттік мәндер үшін Ом заңын аламыз: I =E /Z . Мұндағы Z– тізбектің комплекстік кедергісі: Z=[ r +j( ωL --1/ωC)]= r+jx = ze^{j φ}. Комплекстік кедергінің нақты бөлігі активті кедергіге r, ал жорамал бөлігі реактивті кедергіге x = ( ωL --1/ωC) тең. Комплекстік кедергінің модулі .

Комплекстік өткізгіштік деп комплекстік кедергіге кері шаманы айтады:

, , мұндағы ,

- активті өткізгіштік, - реактивті өткізгіштік, - толық өткізгіштік.

Ом заңын комплекстік өткізгіштік арқылы жазайық: I =UY, I =Ug – U b= I_a + I_p.

Сонымен электр тізбегінің толық өткізгіштігі нақты бөлігі активті өткізгіштікке, ал жорамал бөлігі реактивті өткізгіштікке тең комплекс сан ретінде жазылады.

30-сурет

30-суретте көрсетілген тізбектің тармақтарының комплекстік кедергілерін жазайық. Ол үшін алдымен активті және реактивті кедергілердің комплекстік түрде жазылуын көрсетейік: = r, XL , .

X_C

Тізбектің тармақтарының комплекстік кедергілері:

Тізбектің толық комплекстік кедергісі:

Комплекстік қуат деп кернеудің комплекстік әрекеттік мәнін түйіндес токтың комплекстік әрекеттік мәніне көбейткенге тең: Ỉ. Берілген комплекстік токқа түйіндес токтың модулі осы токтың модулімен бірдей, ал фазасы қарама-қарсы болып келетін токты айтады. Айталық, - берілген ток болса, онда түйіндес ток Ỉ .

Егер болған жағдайда , мұндағы

P = UIcosφ - активті қуат; = UIsinφ - реактивті қуат. Бұдан комплекстік қуаттың нақты бөлігі активті қуатқа тең, ал жорамал бөлігі реактивті қуатқа тең.

Комплекстік қуаттың көрсеткіш түрде жазылуы: =se^jφ, мұндағы , .

Синусоидалы ток тізбегіндегі қуаттар тепе-теңдігі мынаны білдіреді: біріншіден, тізбектегі барлық қоректендіргіштердің активті қуаттарының алгебралық қосындысы сол тізбектегі резистивті элементтердің активті қуаттарының арифметикалық қуаттарының қосындысына тең:

∑U_қорI_қор cos(φ_u – φ_i)= ∑rI_r ² немесе ∑P_қор = ∑P_r ,

екіншіден, тізбектегі барлық қоректендіргіштердің реактивті қуаттарының алгебралық қосындысы сол тізбектегі индуктивті элементтердің реактивті қуаттарының арифметикалық қосындысы мен сыйымдылық элементтердің реактивті қуаттарының арифметикалық қосындысының айырмасына тең: ∑U_қорI_қор sin(φ_u – φ_i)= ∑x_LI² _L -∑ x_CI² _C , немесе ∑Q_қор =∑Q_L - ∑Q_C.

Қоректендіргіштердің активті және реактивті қуаттарының алгебралық қосындысының қосылғыштарының таңбасы токтың оң бағыты э.қ.к.-тің бағытымен сәйкес болған жағдайда плюс болады, егер, ал керісінше жағдайда минус болады. Қуаттар тепе-теңдігін комплекс түрде өрнектеуге болады: ∑ _қор =∑ _қаб, немесе ∑ _қор =∑U_қор Ỉ_қор = ∑P_қор +j∑Q_қор , ∑ _қаб =∑U_қаб Ỉ_қаб= ∑P_қаб +j∑Q_қаб. Сондықтан ∑P_қор = ∑P_қаб, ∑Q_қор = ∑Q_қаб.

Топографиялық диаграммада оның белгілі бір нүктесіне тізбек сұлбасының белгілі бір нүктесінің комплекстік потенциалы сәйкес келеді. Потенциалы нөлге тең деп алынған сұлба нүктесі координаталар басына тура келеді. Топографиялық диаграмма тізбектің кез-келген нүктелерінің арасындағы кернеуді оңай анықтауға мүмкіндік береді. Ол үшін диаграммадағы тиісті нүктелерді түзумен қосады.

Негізгі әдебиеттер: [1(83-91, 97-102), 3(172-209)]

Қосымша әдебиеттер: [5,6,7,8]

Бақылау сұрақтары:

1.Синусоидалы токтың комплекстік мәндері үшін Ом және Кирхгоф заңдары.

2.Комплекстік кедергі. Комплекстік өткізгіштік.

3.Комплекстік қуат. Қуаттар тепе –теңдігі. Қуатты ваттметрмен өлшеу.

4. Топографиялық диаграммаға түсініктеме беріңіз.

№ 10 Дәріс.Екіұштылардың жиіліктік сипаттамалары. Кернеулер резонансы. Токтар резонансы

Екіұштық бір немесе бірнеше индуктивтіліктен және бір немесе бірнеше сыйымдылықтан тұрады делік. Мұндай екіұштықтың резонанстық режимі деп осы екіұштықтың кірістік кедергісі тек активті сипатта болып, реактивті кедергі немесе реактивті өткізгіштік нөлге тең болған жағдайды айтамыз. Басқаша айтқанда, сыртқы тізбекке қатысты екіұштық өзін резонанстық режимде активті кедергі секілді сезінеді. Сондықтан соның кірісіндегі кернеу және токтың фазалары бір-біріне сәйкес келеді. Ал екіұштықтың бұл кездегі реактивті қуаты нөлге тең болады. Резонанстық режимді екі түрге бөледі: кернеулер резонансы және токтар резонансы.

Электр тізбегінде кернеулер резонансы болу үшін мынадай екі шарт бір мезгілде орындалуы қажет: 1) r, L, C - элементтері тізбектей жалғануы керек; 2) индуктивті кедергі x_L сыйымдылық кедергіге x_C тең болу керек.

Резонанс кезінде:

а) Тізбектің толық кедергісі: , яғни толық кедергі, біріншіден, активті кедергіге тең болады, екіншіден, оның мәні минималды болады; ә) Тізбектегі ток: I= U/z = U/r, демек токтың мәні максималды болады; б) Фазалық ығысу: , яғни қоректендіргіштің кернеуі мен токтың векторлары бір түзудің бойында жатады; в) Тізбектің элементтеріндегі кернеулер: U_a =Ir=(U/r)r=U, яғни активті кернеу толық кернеуге тең болады; индуктивті кернеу U_L =Ix_L =(x_L /r)U , сыйымдылық кернеу U_C =Ix_C =(x_C /r)U ; x_L =x_C болғандықтан U_L = U_C,, демек, резонанс кезінде индуктивті кернеу сыйымдылық кернеуге тең болады, ал реактивті кернеу U_p =U_L - U_C =0;

Егер x_L= x_C >>r болса, онда U_L= U_C >U, яғни резонанс кезінде реактивті элементтердегі кернеу тізбекке берілген кернеуден бірнеше есе көп болуы мүмкін. Бұл апаттық жағдай тудыруы мүмкін.

31-сурет

г) Резонанс кезіндегі токтың және элементтердегі кернеулердің векторларың өзара орналасуы 31-суреттегі векторлық диаграммада көрсетілген; д) Резонанстық бұрыштық жиілік: ω0=1/ , резонанстық жиілік ƒ0=1/2π ; е) Сипаттамалық кедергі деп индуктивті кедергінің xL немесе сыйымдылық кедергінің xC резонанс кезіндегі мәнін айтады

ж) Контурдың сапалылығы: ; з) Өшу коэффициенті: , демек, ол сапалылыққа кері шама; и) Қуаттар: активті қуат P= I²r, индуктивті қуат Q_L= x_LI², сыйымдылық қуат Q_C= x_CI², реактивті қуат Q_р= Q_L - Q_C=0, яғни резонанс кезінде реактивті қуат нөлге тең болады. Сонымен кернеулер резонансы кезінде ток максималды, ал x_L= x_C, U_L= U_C, Q_L= Q_C.

r, L, C элементтері бірізді жалғанған тізбектің жиілік сипаттамалары. Мұндай тізбектегі ток:

. Егер ω =0 немесе ω = ∞ болса, онда болады. Ал ω₀ = 1/ болса, онда ток I=U/r максималды болады. Айталық, 0<ω<∞. Онда индуктивті кернеу: .

Егер , онда , ал егер онда . -дің қандай жиілікте максималды болатындығын анықтау үшін бөлшектің бөлімін минимумға зерттейміз. Ол үшін бөлімнен бірінші ретті туынды алып, оны нөлге теңестіріп, -дің максималды болатын жиілігін табамыз: > . Бұл жиілікте максималды мән >U_L0. U_L0 – кернеу резонансы кезіндегі мәні.

С ыйымдылық элементтегі кернеу .

Бұл өрнектің бөлімнен бірінші ретті туынды алып, оны нөлге теңестіріп, U_C-дің максималды болатын жиілігін табамыз: < ω₀. Бұл жиілікте -дің максималды мәні =U_Lmax. Егер , онда ,ал болса, онда .

Сонымен U_C максималды болатын жиілік ω_С резонанстық жиіліктен ω₀ кіші болады, ал -дің максималды болатын жиілігі ω_L резонанстық жиіліктен ω₀ үлкен болады. Контурдың сапалылығы Q неғұрлым үлкен болған сайын, соғұрлым ω_С пен ω_L мәндері ω₀-ден азырақ ауытқиды және резонанстық қисықтар тігірек, үшкірлеу болады (32- сурет).

Т октар резонансы тізбекте мынадай шарттар бір мезгілде пайда болғанда болады: а) r, L, C элементтері параллель жалғануы керек (24-сурет); ә)сыйымдылық өткізгіштік b_L индуктивті өткізгіштікке b_C тең болуы керек, яғни b_L=b_C.

Резонанс кезінде:а) Тізбектің толық өткізгіштігі , яғни толық өткізгіштік минималды, ал толық кедергі максималды болады;

ә) Тізбектің толық тогы =Ug, демек ток минималды болады.

б ) Фазалық ығысу ;

в) Тізбектің тармақтарындағы токтар: I_a= Ug, I_L=Ub_L,, I_C=Ub_C , яғни I_L= I_C,. Реактивті ток I_р=I_L-I_C=0. Ал I=Uy=Ug=I_a, демек ,толық ток активті токқа тең. г) 33-суреттегі диаграммада резонанс кезіндегі токтардың векторларының өзара орналысуы көрсетілген; д) резонанстық жиілік ƒ₀=1/2π ; е) Қуаттар: активті қуат P= U²g, индуктивті қуат Q_L= U²b_L, сыйымдылық қуат Q_C= U²b_C, демек Q_L= Q_C; Реактивті қуат Q_p= Q_L - Q_C= 0;

34-суретте параллель контурдың жиіліктік сипаттамасының қисықтары көрсетілген. Сыйымдылық элементтегі ток I_C =ωCU жиілікке пропорционал өседі, ал индуктивті элементтегі ток I_L=U/ωL жиілікке кері пропорционал өзгереді. Резистивті элементтегі ток I_r=U/r жиілікке тәуелді емес. I_C мен I_L қисықтарының қиылысқан нүктесі токтар резонансына сәйкес келеді. Бұл жағдайда I=I_r.

Реалды жағдайда 24-суреттегі индуктивті элемент пен активті кедергі r₂, ал сыйымдылық элемент пен активті кедергі r₃ бірізді жалғануы мүмкін. Бұл кедергілер арқылы сымдардағы энергия шығыны есепке алынады. Мұндай тізбекте токтар резонансы болу шарты: b_L=b_C, , бұдан резонанстық бұрыштық жиілік .

Бұл жағдайда да резонанс кезінде толық ток пен кернеумен фаза бойынша сәйкес келеді.

Негізгі әдебиеттер: [1(113-123, 97-102), 2(223-234)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1.Екіұштықтың резонанстық режим кезіндегі жұмыстарына тоқталыңыз. Резонанстық режим деген қандай режим және оның қандай түрлері бар?

2. Активті және реактивті элементтерді тізбектей қосқанда байқалатын кернеулер резонансына түсініктеме беріңіз. Кернеулер резонансы кезінде тізбекті сипаттайтын электрлік параметрлердің мәндері мен сипаттары қандай өзгеріске түседі?

3. Токтар резонансына түсініктеме беріңіз. Резонансы кезіндегі тізбектің толық өткізгіштігін, тізбек тармақтарындағы токтарды және фазалық ығысуды сипаттаңыз.

4.Резонанстық жиіліктік сипаттамаға түсініктеме беріңіз.

№11 Дәріс. Индуктивті байланысқан элементтері бар тізбектер

Тізбектің бір контурында немесе бір элементінде ток өзгерген кезде басқа контурда немесе басқа элементте э.қ.к. пайда болса, онда осы екі контурды немесе екі элементті бір-бірімен индуктивті байланысқан (магнитті байланысқан) дейді, ал екінші контурда немесе екінші элементте пайда болған э.қ.к.-ті өзаралық индукцияның э.қ.к.-і деп атайды.

Өзара қатар ораласқан, орам сандардары w₁ және w₂ тең екі индуктивтілік орамалармен i₁ және i ₂ токтары жүрсе, онда әр ораманың барлық магнит сызықтары екінші ораманың орамдарымен ілінісуі мүмкін, яғни Ф₂₁ =Ф₁₁, Ф₁₂ =Ф₂₂. Сондықтан мұндай тізбектерді талдау кезінде орамалардың өздерінің ағын ілінісулерінен ( Ψ₁₁ және Ψ₂₂) басқа қосымша ағын ілінісулерін ( Ψ₁₂ және Ψ₂₁) есепке алу керек. Бірінші ораманың өзіндік ағын ілінісуі Ψ₁₁=Ф₁₁ w₁=L₁ i₁, бірінші ораманың тогының әсерінен пайда болған екінші орамадағы қосымша ағын ілінісуі Ψ₂₁= Ф₂₁ w₂=Ф₁₁ w₂=М₂₁ i₁ , мұндағы М₂₁= Ψ₂₁/i₁ –пропорциональдық коэффициент, өзаралық индуктивтілік деп аталады. Бұл өрнектерден

L₁/ М₂₁= w₁/ w₂.

Екінші ораманың өзіндік ағын ілінісуі Ψ₂₂=Ф₂₂ w₂=L₂ i₂, екінші ораманың тогының әсерінен пайда болған бірінші орамадағы қосымша ағын ілінісуі Ψ₁₂= Ф₁₂ w₁=Ф₂₂ w₁=М₁₂ i₂ . Бұл өрнектерден L₂/ М₁₂= w₂/ w₁. Көрсетілген екі қатынастан М₁₂ М₂₁= L₁L₂ екендігін көруге болады. Тәжірибе М₁₂ = М₂₁=М екендігін көрсетеді. Демек, өзаралық индуктивтілік М= .

Егер бір ораманың магнит сызықтарының тек біраз бөлігі ғана екінші орамамен ілініссе, яғни Ф₂₁ <Ф₁₁, Ф₁₂ <Ф₂₂ болса, онда өзаралық индуктивтілік М=К , мұндағы К= М / - байланыс коэффиценті деп аталады. Бұл коэффициенттің мәні бірден кіші К<1, өйткені Ф₂₁ <Ф₁₁, Ф₁₂ <Ф₂₂, яғни бір ораманың магнит ағыны екінші ораманы толық қамтымайды.

­Өзаралық индуктивтілік токтардың мәндері мен бағыттарына тәуелді емес , ол орамалардың құрылысымен және өзара орналасуымен анықталады. Қарастырылған екі ораманың толық ағын ілінісуі Ψ екі құраушыдан тұрады. Құраушылар токтардың бағыттарына және өзара орналасуына байланысты қосылуы немесе бірі бірінен алынуы мүмкін. Сұлбада орамалардың аттас ұштарын ( қысқыштарын) нүктелер арқылы белгілейді (35-сурет). Егер токтар бағыттары орамалардың аттас ұштарына байланысты бірдей болса, онда орамалар өзара үйлесімді қосылған (35а-сурет). Бұл жағдайда бірінші ораманың толық ағын ілінісуіΨ₁= Ψ₁₁+ Ψ₁₂, ал екінші ораманың толық ағын ілінісуі Ψ₂= Ψ₂₂+ Ψ₂₁.Егер токтар бағыттары орамалардың аттас ұштарына байланысты бірдей болмаса, онда орамалар өзара қарсы қосылған (35ә-сурет). Бұл кезде бірінші ораманың толық ағын ілінісуі Ψ₁= Ψ₁₁ - Ψ₁₂, ал екінші ораманың толық ағын ілінісуі Ψ₂= Ψ₂₂ - Ψ₂₁.

Өзаралық индукцияның э.қ.к.-і. Егер өзаралық ағын ілінісуі уақытқа тәуелді өзгерсе, онда орамаларда өзаралық индукцияның э.қ.к.-тері пайда болады: е_2м= -dΨ₂₁ /dt , немесе е_2м= -Mdi₁/dt, ал бірінші орамада е_1м= -dΨ₁₂ /dt, немесе е_1м=- Mdi₂/dt. Екінші орамада пайда болған өзіндік индукция э.қ.к.-і бірінші орамадағы токтың өзгерісіне қарсы әсер етеді.

а) б) 35-сурет а) ә) б) 36-сурет

Индуктивті байланысқан элементтер бірізді жалғанған тізбек (36а-сурет). Тізбек бірізді қосылған r1 мен r2 активті кедергілерден және L1 мен L2 индуктивтіліктен құралсын. Индуктивті элементтер арасындағы магниттік байланысты өзара индуктивтілік М сипаттайды. Оларды тізбекке қосудың екі сұлбасы болуы мүмкін. Индуктивтілік орамаларды үйлесімді қосқан кезде олардың аттас ұштарымен салыстырғанда тізбектегі ток бір бағытта жүреді. Сондықтан әр индуктивті элементпен ілінісетін өзіндік индукцияның және өзара индукцияның магнит ағындары қосылады. 36а–суретте көрсетілген тізбек үшін Кирхгоф екінші заңы бойынша теңдеу құрайық. Егер токтар бағыттары орамалардың аттас ұштарына байланысты бірдей болмаса, онда орамалар өзара қарсы қосылған. Бұл жағдайда бірінші ораманың толық ағын ілінісуі Ψ1= Ψ11 - Ψ12, ал екінші ораманың толық ағын ілінісуі Ψ2= Ψ22 - Ψ21. Ir1+L1 di/dt + M di/dt+L2 di/dt+ M di/dt+ir2 =e. Комплекстік түрде: I [r1+r2+jω(L1+L2+2M)]=E. Бұдан орамалар үйлесімді қосылған кездегі олардың толық индуктивтілігін анықтаймыз: Lүйл =L1+L2+2M. Тізбектің толық кедергісі Zүйл= r1+r2+jω(L1+L2+2M)=Z1+Z2+2Zm, мұндағы Z1=r1+ jωL1, Z2= r2+jωL2,, Zm= jωM.-орамалардың комплекстік кедергілері және өзара индукцияның комплекстік кедергісі. Орамалар үйлесімді қосылған жағдайға сәйкес келетін векторлық диаграма 36ә–суретте көрсетілген. Орамаларды қарсы қосқан кезде олардың аттас ұштарымен салыстырғанда тізбектегі ток қарама-қарсы бағытта жүреді. Сондықтан әр индуктивті элементпен ілінісетін өзіндік индукцияның және өзара индукцияның магнит ағындары бір-біріне қарсы бағытталады, яғни толық магнит ағыны азаяды. Бұл жағдайда Кирхгофтың екінші заңы

бойынша құрылған теңдеу:

Ir₁+L₁ di/dt - M di/dt+L₂ di/dt- M di/dt+ir₂ =e.

Комплекстік түрде: I [r₁+r₂+jω(L₁+L₂ -2M)]=E

Орамалар қарсы қосылған кездегі олардың толық индуктивтілігін анықтаймыз: L_қар =L₁+L₂ -2M. Тізбектің толық кедергісі Z_қар= r₁+r₂+jω(L₁+L₂ -2M)=Z₁+Z₂ - 2Z_m,

36б -суретте орамалардың қарсы қосылған сұлбасына сәйкес келетін векторлық диаграмма көрсетілген.

Индуктивті байланысқан элементтер параллель жалғанған тізбек. Өзара индуктивтігі М, кедергілері r₁ мен r₂ , ал индуктивтері L₁ мен L₂ болатын екі қабылдағыш параллель қосылған.

37-сурет

Орамалардың аттас ұштары бір түйінге қосылған (37 -сурет). Токтар мен кернеулердің таңдап алынған оң бағытында I=I1+I2; U=Z1I1+Zm I2; U=ZmI1+Z2 I2, ,мұндағы Z1=r1+ jωL1,, Z2=r2+jωL2,, Zm=jωM. Бұл теңдеулерді шешкенде ; ; ;

Бұдан тізбектің комплекстік кедергісі .

Тізбектің толық индуктивтігі L_үйл . Тармақтар арасында индуктивтік байланыс болмаған жағдайда, яғни Z_m=0 болғанда, бұл өрнек мына түрге келеді: .

Егер орамалардың аттас ұштары әр түйінге қосылған болса, яғни орамалар қарсы қосылған жағдайда, кернеудің теңдеуіндегі Z_m таңбасы минусқа өзгереді. Демек, бұл жағдайда тізбектің кірістік комплекстік кедергісі , ал толық индуктивтілігі L_қар .

Индуктивті байланысқан элементтер бар күрделі тізбекті есептеу. Мұндай тізбектерді есептеу үшін Кирхгоф екінші заңы бойынша теңдеулер құрған кезде, индуктивті орамалар үшін жазылатын кернеулердің өрнегіне өзара индукцияның комплекстік кернеуін jωMI қосу керек. Егер орамалар үйлесімді қосылса, онда бұл комплекс оң таңбалы, ал қарсы қосылған жағдайда теріс таңбалы болады.

Индуктивті байланысқан элементтері бар тізбекті индуктивті байланысы жоқ балама сұлбамен ауыстыру арқылы тізбекті есептеуді жеңілдетуге болады. Екі элементтен (Z₁ және Z₂) тұратын индуктивті байланысы бар тізбекті балама сұлбамен ауыстырғанда Z₁ мен Z₂ кедергілеріне Z_м кедергісі жалғанады және олар мен жаңа пайда болған түйін арасына Z_м кедергісі қосылады. Егер индуктивті байланысқан үш элементтер үш сәулелі жұлдызша немесе ұшбұрыш арқылы жалғанған болса , онда жоғарыда келтірілген тәсіл бойынша индуктивті байланыстан құтылып, оған балама сұлбаға көшуге болады.

Темір өзекшесіз трансформатор (ауа трансформаторы). Трансформатор деп тізбектегі энергияны басқа тізбекке электромагниттік индукция құбылысы арқылы беретін аппаратты айтады.

Оның қарапайым түрі ферромагниттік өзекшесіз индуктивті байланысқан екі орамадан тұрады. Кернеу көзі бірінші орамаға қосылады, ал жүктеме екінші орамаға қосылған.

Трансформатордың теңдеулері мына түрде жазылады:

Мұндағы r₁ , L₁ және r₂ , L₂ – бірінші және екінші орамалардың активті кедергілері және индуктивтері; Z _қ =r_қ +jX_қ –жүктеменің кедергісі; I₁, I₂ – бірінші және екінші орамадағы токтар.

Екінші орамадағы ток: I₂ =-jX_m I₁ /( r_2қ +jX_2қ ). Токты трансформациялау коэффициенті: k_i=I₂ /I₁ =X_m /z_2қ . Кернеуді трансформациялау коэффициенті: k_u =U₂ / U₁ . Егер L₁ <M<L₂ болса,онда L₁ -M теріс, яғни сиымдылық сипатта болады. Бұл жағдайда U₂ >U₁ , демек, трансформатор кернеуді жоғарлатады. Егер L₁ >M>L₂ болса,онда L₂ -M теріс, яғни сиымдылық сипатта болады. Бұл жағдайда U₂ <U₁ , демек, трансформатор кернеуді төмендетеді.

Негізгі әдебиеттер: [1(124-144), 3(278-302)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1.Тізбектің индуктивті байланыстағы элементтері жөнінде түсініктеме беріңіз. Байланыс коэффициенті қалай анықталады?

2. Өзара индукцияның э.қ.к.-і дегеніміз не? Орамалардың өзара үйлесімді және қарсы қосылуы туралы түсініктеме беріңіз.

3. Индуктивті байланысқан элементтері бірізді жалғанған тізбекті есептеу жұмысы қалай жүргізіледі? Векторлық диаграммасына түсініктеме беріңіз

4. Индуктивті байланысқан элементтері параллель жалғанған тізбекті есептеу жұмысы қалай жүргізіледі? Векторлық диаграммасына түсініктеме беріңіз

5. Темір өзекшесіз трансформатор (ауа трансформаторы туралы түсініктеме беріңіз.

№12 Дәріс. Үш фазалы қоректендіргіштер және үш фазалы тізбектер туралы түсініктемелер. Қоректендіргіш пен қабылдағыштың фазалары жұлдызша сұлбасы бойынша жалғанған үш фазалы тізбек

Электр тізбегінің көп фазалы жүйесі деп жиіліктері бірдей, ал фаза бойынша бірі бірінен ығысқан бірнеше айнымалы э.қ.к-тер тізбектерінің жиынтығын айтады. Көбінесе практикада амплитудалары тең және фазалары бойынша 2π/т – бұрышқа ығысқан ( мұндағы т-фаза саны) бірнеше э.қ.к.-терден тұратын көп фазалық симметриялық жүйелер қолданылады. Қазіргі кезде көп фазалық жүйелердің ішінде ең көп тарағаны -үш фазалы жүйелер.

Үш фазалы симметриялы э.қ.к.-тер жүйесі деп бірдей жиілікті және бірдей амплитудалы, ал фаза бойынша 120⁰ ығысқан үш синусоидалы э.қ.к.-тердің жиынтығын айтады.

Үш фазалы симметриялы э.қ.к.-тер жүйесін алу үшін үш фазалы синхронды генератор қолданылады. Оның статорында бірі бірінен 120⁰-қа ығысқан және өзара оқшауланған үш фазалық орама орналасқан. Ротор айналғанда осы орамаларда амплитудалары бірдей, жиіліктері бірдей, бірақ фаза бойынша 120⁰- қа ығысқан үш э.қ.к.-тер пайда болады. Олардың біреуін е_А (Е_А ), одан фаза бойынша 120⁰ кеш қалған екіншісін е_В (Е_В), ал біріншіден фаза бойынша 120⁰ озған э.қ.к.-і е_С (Е_С) белгілейміз.

Генератордың орамаларын оның фазалары деп атайды да, А,В,С латын әріптері арқылы белгілейді. Фазалар кезектесуі деп э.қ.к.-тердің белгілі бір мәнге ие болу кезіндегі ретін айтады . Егер бұл рет Е_А , Е_В , Е_С болса, онда мұндай кезектесу тура кезектесу деп аталады.

Симметриялы генератордың фазалық орамаларының э.қ.к.-тердің лездік мәндері:

е_А =Е_тsinωt, е_В =E_msin(ωt-120⁰), е_С=E_msin(ωt+120⁰).

Э.қ.к.-тердің комплекстік әрекеттік мәндері: Е_А =Е_фе^j0˚, E_B= Е_фе ^-j120˚, E_C= Е_фе ^j120˚ .

Э.қ.к.-тердің комплекстік әрекеттік мәндерінің алгебралық қосындысы нөлге тең және э.қ.к.-тердің лездік мәндерінің алгебралық қосындысы да нөлге тең: Е_А+E_B+E_C=0; е_А+ е_В+ е_С =0.

Ү ш фазалы тізбек деп үш фазалы э.қ.к.-тер жүйесі мен үш фазалы қабылдағыштың ( жүктеменің) және жалғау сымдарының жиынтығын айтады. Үш фазалы тізбектің фазасы деп оның бойымен белгілі бір ток ғана жүретін бөлігін айтады. Үш фазалы жүйе алу үшін генератордың мен жүктеменің фазаларын өзара әр түрлі сұлба бойынша қосады:

1.Алты сым арқылы жалғану сұлбасы (38-сурет). А, В,С- генератор орамаларының басқы ұштары; x,y,z- орамалардың аяққы ұштары;

Бұл сұлба бойынша генератордың әр фазасы жүктеменің әр фазасымен екі сым арқылы жалғанады. Барлығы алты сым керек болады.. Бұл сұлба экономикалық жағынан тиімсіз.

2 .Жұлдызша сұлба бойынша жалғағанда ораманың аяққы ұштары x,y,z бір нүктеге ( түйінге) қосылады және ол нүктені үш фазалы қоректендіргіштің нөлдік нүктесі немесе бейтарап нүктесі ( О) деп атаймыз(39а-сурет). Сол сияқты жүктеменің де фазаларының бір ұштары бір нүктеге ( түйінге) қосылады және ол нүктені жүктеменің нөлдік нүктесі немесе бейтарап нүктесі ( О′) деп атаймыз. Генератордың орамаларының басқы ұштарын жүктемемен қосатын сымдарды желілік сымдар деп атайды, ал олар арқылы жүретін токтар желілік токтар I_A , I_B, I_C деп аталады. Бұл токтар генератордан жүктемеге қарай бағытталған. Генератордың бейтарап нүктесін жүктеменің бейтарап нүктесімен жалғайтын сымды нөлдік немесе бейтарап сым деп аталады. Бейтарап сыммен жүретін ток нөлдік ток (I₀) немесе бейтарап ток деп аталады және ол жүктемеден генераторға карай бағытталады.

Үш фазалық жүйеде генератордың фазалық орамаларының ұштарының арасындағы немесе жүктеменің фазаларының ұштарының арасындағы кернеулерді (U_A, U_B ,U_C ) фазалық кернеулер деп аталады. Бұл кернеулерді желілік сымдар мен нөлдік сым арасындағы кернеулер деп де қарастыруға болады. Симметриялы жүйеде фазалық кернеулердің әрекеттік мәндері бірдей болады: U_A =U_B=U_C = U_ф.

Фазалық токтар деп генератордың фазалық орамалары немесе жүктеменің фазалары арқылы жүретін токты айтады.

Желілік кернеулер (U_AB, U_BC ,U_CA ) деп желілік сымдар арасындағы кернеулерді айтамыз. Желілік кернеулерді фазалардың бастапқы ұштарының арасындағы кернеулер деп де қарастыруға болады. Симметриялы жүйеде желілік кернеулердің әрекеттік мәндері бірдей болады: U_AB = U_BC = U_CA = U_ж .

Егер U_A = Е_А , U_B = E_B , U_C = E_C ескерсек, онда желілік кернеулердің комплекстік мәндері: U_AB = Е_А - E_B = U_A - U_B = U_ж e^j30˚ , U_BC= E_B- E_C= U_B- U_C = U_ж e ^–j90˚ , U_CA= E_C- E_A= U_C- U_A = U_ж e ^j150˚ .

Үш фазалы симметриялы қоректендіргіштің фазалары жұлдызша жалғанған кезде фазалық және желілік кернеулер үшін векторлық диаграмма 39ә – суретте көрсетілген. Бұл диаграммадан фазалық және желілік кернеулердің комплекстік мәндері үш бірдей теңбүйірлі үшбұрыш құрайтындығын көреміз. Бұл үшбұрыштан желілік және фазалық кернеулердің әрекеттік мәндері өзара мынадай қатынаста болатындығын көреміз: U_ж =2U_Фcos30˚= .

Қоректендіргіш пен қабылдағыштың ( жүктеменің) фазаларының токтары: I=E_A/Z_A =U_A/ Z_A, I_B= E_B/Z_B= U_B/ Z_B, I_C= E_C/Z_C= U_C/ Z_C. Бейтарап сымдағы ток I₀ = I_A + I_B + I_C. Қоректендіргіш пен қабылдағыштың ( жүктеменің) фазалары жұлдызша сұлба бойынша жалғанса, желілік токтар оларға сәйкес фазалық токтарға тең болады.

Егер жүктеме симметриялы болса, яғни оның фазаларының кедергілері бір біріне тең болса (Z_A= Z_B = Z_C) болса, онда =0, яғни нөлдік сыммен ток жүрмейді. Бұл жағдайда нөлдік сымды сұлбадан алып тастауға болады және желілік пен фазалық токтардың әрекеттік мәндері тең: I_Ж=I_Ф.

Негізгі әдебиеттер: [1(156-168), 3(378-393)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1. Үш фазалы симметриялы э.қ.к.-тер жүйесі туралы түсініктеме беріңіз.

2. Желілік және нөлдік (бейтарап) сымдар, желілік және фазалық кернеулер мен токтардың анықтамасына тоқталыңыз.

3. .Қоректендіргіш пен қабылдағыштың фазаларының жұлдызша сұлбасы бойынша жалғануын қарастырып, векторлық диаграмманы тұрғызыңыз. Бейтарап сымның қызметіне тоқталыңыз.

4 Үш фазалық симметриялы жүйедегі желілік және фазалық кернеулер, токтар арасындағы қатынастар қандай түрде болады?

№13 Дәріс. Қоректендіргіш пен қабылдағыштың фазаларының үшбұрыш сұлбасы бойынша жалғануы. Нөлдік сымсыз жұлдызша сұлбасы бойынша жалғанған үш фазалы тізбектегі симметриялы емес режим және оны есептеу

Қоректендіргіштің фазаларын үшбұрыш сұлбасы бойынша қосу үшін бір фазаның аяқы ұшын екінші фазаның басқы ұшымен, екінші фазаның аяқы ұшын үшінші фазаның басқы ұшымен, ал үшінші фазаның аяқы ұшын бір фазаның басқы ұшымен қосады (40-сурет). Сұлбада бейтарап сым болмайды. Сондықтан қоректендіргіштің желілік кернеулері оның фазалық кернеулеріне тең болады:

Егер U_AB = Е_А , U_BC = E_B , U_CA = E_C. Ом заңы бойынша қабылдағыштың фазалық токтары:

I_АВ= /Z_AВ =U_AВ/ Z_AВ, I_BС= E_B/Z_BС= U_BС/ Z_BС, I_CА= E_C/Z_CА= U_CА / Z_CA.

Егер қабылдағыш симметриялы (Z_AВ= Z_BС = Z_CА) болса, онда барлық фазалық токтардың әрекеттік мәндері бірдей болады және олардың желілік кернеулерге байланысты фазалық ығысулары да бірдей болады.

Кирхгофтың бірінші заңы бойынша желілік токтар: I_A= I_AB - I_CA, I_B= I_BC - I_AB, I_C= I_CA - I_BC. Бұл желілік және фазалық токтардың комплекстік мәндері үшін құрылған векторлық диаграмадағы токтар үшбұрышынан желілік токтардың модулдері мен фазалық токтардың модулдері арасында мынадай байланыс барынан көрінеді:

I_ж =2I_Фcos30˚= I_Ф.

Үш фазалы тізбектің операторы деп модулі 1-ге тең, фазасы 120⁰-қа тең комплекс санды атайды. Оны , , ;Үш вектор 1, а, а² симметриялы үш фазалы жүйе құрайды (41-сурет), сондықтан ; Кез-келген векторды операторға а көбейткенде ол вектордың модулі өзгермейді, бірақ ол 120⁰-қа бұрылады. Ал векторды а² көбейтсек, онда ол 240⁰ бұрылады. Операторды а пайдаланып E_B және E_C –ні E_A арқылы өрнектеуге болады: E_B=a² E_A, E_C= aE_A (42-сурет).

Нөлдік сымсыз жұлдызша сұлбасы бойынша жалғанған симмериялы емес үш фазалы тізбек (43-сурет). Егер жүктеме симметриялы емес (Z_A ≠Z_B ≠Z_C) болса, сұлбаның екі түйіні ( О және О′ нүктелері) арасында потенциалдар айырымы - U_00′ кернеуі пайда болады. Бұл кернеуді анықтау үшін екі түйіндік потенциалдар тәсілін қолданамыз. Бұл тәсіл бойынша:

U_00′ = (Е_А Y_A + E_B Y_B + E_C Y_C)/( Y_A+ Y_B+ Y_C)= =(Е_А Y_A+ +a² E_A Y_B +a E_A Y_C)/( Y_A+ Y_B+ Y_C)= =Е_А (Y_A + a²Y_B +a Y_C)/( Y_A+ Y_B+ Y_C), мұндағы Y_A=1/Z_A, Y_B=1/Z_B, Y_C=1/Z_C – жүктеменің фазаларының комплекстік өткізгіштері.

Желілік токтарды анықтаймыз: I_A =U_A0′ / Z_A , I_B = U_B0′ / Z_B , I_C= U_C0′ / Z_C .

Бұл өрнектердегі кернеулер

U_A0′ = Е_А- U_00′ , U_B0′ = Е_B- U_{00′ ,} U_С0′ = Е_С- U_00′ .

Егер Z_A = Z_B = Z_C болса, онда Y_A = Y_B= Y_C=Y. Сондықтан U_00′ =Е_А Y (1 + a² +a )/3 Y =0.

Бұл жағдайда U_A0′ = Е_А, U_B0′ = Е_{B ′}, U_C0′ = Е_С , сол себепті де I_A = Е_А / Z_A , I_B = Е_B / Z_B , I_C= Е_С / Z_C;

Негізгі әдебиеттер: [1(156-168), 3(378-393)]

Қосымша әдебиеттер: [ 4,6,7,9,14 ]

Бақылау сұрақтары:

1.Қоректендіргіш пен қабылдағыштың фазаларының үшбұрыш сұлбасы бойынша жалғануына түсініктеме беріңіз. Токтар үшін векторлық диаграмма тұрғызыңыз.

2. Желілік токтарды фазалық токтар арқылы қалай табуға болады? Жүйе симметриялы болған кезде желілік токтардың модульдары мен фазалық токтардың модульдарының арасындағы қатынас қандай болады?

3. Үш фазалы тізбектің операторы дегенімз не? Оператор арқылы симметриялы э.қ.к.-тер қалай бейнелінеді?

4. Нөлдік сымсыз жұлдызша сұлбасы бойынша жалғанған симмериялы емес үш фазалы тізбек туралы түсініктеме беріңіз және есеп тәсіліне тоқталыңыз.

5. Осы тізбек симметриялы болса, онда есептеу жұмысы қалай жүргізіледі?

№14 Дәріс. Үш фазалы тізбектердің қуаттары және оларды өлшеу. Өзара индуктивті байланысқан элементтері бар үш фазалы тізбектер. Үш фазалы желінің балама сұлбасы

Үш фазалы тізбектің активті қуаты жүктеменің фазаларының активті қуаттарының және нөлдік сымның кедергісінде бөлінетін активті қуаттың қосындысына тең:

,[Вт].

Үш фазалы тізбектің реактивті қуаты:

, [ВАр].

Толық қуат: , [ВА].

Жүктеме симметриялы болса болса, онда: , , , .

Фазалық активті қуат: ; Фазалық реактивті қуат: . Үш фазалы тізбектің активті және реактивті қуаты: , .

Үш фазалы тізбектің толық қуаты: ;

Жүктеменің фазаларының өзара жалғану сұлбаларына ( жұлдызша немесе үшбұрыш) байланыссыз үш фазалы тізбектің қуаттарын желілік кернеу мен желілік ток арқылы анықтауға болады.: , , ;

Үш фазалы тізбектің активті қуатын өлшеу. Егер үш фазалы тізбекте нөлдік сым болса, бірақ жүктеменің фазаларының кедергілері Z_A , Z_B , Z_C бірдей болмаса, онда тізбектің активті қуатын өлшеу үшін үш ваттметр қолданылады (44-сурет).

44-сурет

45-сурет

Тізбектің активті қуаты осы үш ваттметр көрсетуінің қосындысына тең.

Егер тізбектің нөлдік сымы болмаса, онда активті қуатты өлшеу үшін екі ваттметр қолданылады (45-сурет). Бұл екі ваттметрдің көрсетуілері көбінесе бірдей болмайды. Бұл жағдайда үш фазалық жүйенің қуаты екі ваттметрдің көрсетулерінің алгебралық қосындысына тең.

Айталық, бірінші ваттметрдің көрсетуі P₁=Re[U_AC Ī_A] , ал екінші ваттметрдің көрсетуі P₂= Re[U_BC Ī_B]. Бұл жағдайда ваттметрлердің көрсетулерінің қосындысы

U_AC Ī_A+ U_BC Ī_B=( U_A - U_C) Ī_A+( U_B - U_C) Ī_B= U_A Ī+U_B Ī_B+ U_C Ī_C.

Соңғы өрнек үш фазаның активті қуаттарының қосындысын көрсетеді.

Егер жүктеме симметриялы болса, онда бір фазаның активті қуатын үшке көбейтеміз.

Өзара индуктивті байланысқан элементтері бар үш фазалы тізбектерді есептеу бір фазалық синусоидалық токтың индуктивтік байланысы бар тізбегінің есебіне ұқсас жүргізіледі.

Үш фазалы желінің балама сұлбасын тұрғызу үшін желінің өнбойында болып жатқан электромагниттік құбылыстар есепке алынуы керек. Магниттік құбылыстарды индуктивтілк, электр өрісііне байланысты құбылыстарды сыйымдылық, ал жылу бөліну құбылысын кедергі арқылы сипаттайды.

Үш фазалы желінің балама сұлбасына оның сымдарының индуктивтілігі және сымдар арасындағы өзара индуктивтілік, сымдар мен жер арасындағы сиымдылық, сымдардың арасындағы сиымдылық, сымдарың активті кедергілері және оқшаулағыштардың ( изоляцияның) өткізгіштері енуі тиіс. 46 –суретте үш фазалы желінің бір фазасының «П » және «Т » тәрізді балама сұлбалары келтірілген. Суретте көрсетілген индуктивтілік L_ф симметриялы үш фазалы желінің индуктивтілігі деп

46- сурет

аталады: L_ф=L_з - М_з. Мұндағы L_з -сымның индуктивтілігі, ал М_з. – сымдар арасындағы өзара индуктивтілік. Желі симметриялы болу үшін, яғни L_з және М_з барлық фазалар үшін бірдей болуы үшін, желінің ұзындығын үшке бөліеді де, сымдардың өзара орналасу ретін әр бөлікте өзгертіп отырады. Бұл тәсілді сымдардың транспозициясы деп аталады.

Суретте көрсетілген сиымдылық С_ф фаза сыйымдылығы деп аталады: С_ф =С_о +3С_м . Мұндағы С_о- сым мен жер арасындағы сыйымдылық, ал С_м – сымдар арасындағы сыйымдылық. Желі сымдарын транспозициялау арқасында С_ф мәні үш фаза үшін бірдей болады.

Суреттегі кедергі R - сымның активті кедергісі. Желі симметриялы болғандықтан бейтарап сыммен ток жүрмейді. Сондықтан бейтарап сымның кедергісі сұлбаға енбеді.

Үш фазалы жүйенің артықшылықтары: а) Электр энергиясын бір фазалық жүйемен алыс қашықтыққа жеткізу үшін қажетті алты сым орнына үш фазалық жүйемен тасымалдағанда небәрі үш сым ғана керек болады, яғни үш фазалық жүйемен тасымалдаған экономикалық жағынан тиімді;

б) Үш фазалы электр қондырғылары құрылысы жағынан қарапайым , бағасы арзан, жұмыс істеуі сенімді болады;