8.4 Расчет прочности сечений, наклонных к продольной оси плиты

Расчет ведем аналогично расчету второстепенной балки.

Прочность железобетонной балки на действие поперечной силы определяем, в первую очередь, проверкой условия:

(8.15)

Определим значение поперечной силы, воспринимаемой сечением без поперечного армирования:

,но не менее (8.16)

где , d — в мм; 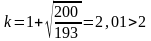, т.е. подставляем максимальное значение 2;

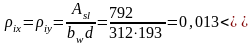0,02 (минимальное значение коэффициента армиро­вания, регламентированное СНБ 5.03.01).

Тогда расчетный коэффициент армирования

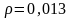
Тогда, с учетом рассчитанных величин получим:

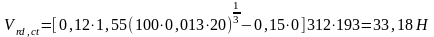
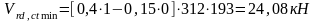
Условие не выполняется, тогда используя метод ферменной аналогии, поперечное армирование определим из условий и

Зададимся углом наклона трещин к горизонтали и шагом поперечной арматуры S=150мм.

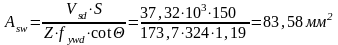
Где Z-расстояние между равнодействующими в сечении:

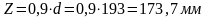
Принимаем четыре стержня диаметром 6мм класса S500 (A_sw=113 мм²) c шагом S=150мм.

При этом должны выполняться условия:

(8.17)

(8.18)

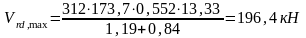
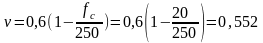
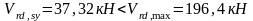-условие выполняется, прочность по сжатой полосе обеспечена.

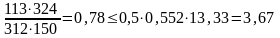-условие выполняется, что означает оптимальность принятого армирования.

8.5 Определение геометрических характеристик приведенного сечения

1. Площадь приведенного сечения.

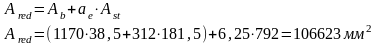(8.19)

Отношение модулей упругости 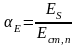(8.20)

где Е_cm=32·10³МПа– модуль упругости бетона класса С20/25 марки П2 по удобоукладываемости (таблица 6.2[2]).

Еs=20·10⁴ МПа – модуль упругости для ненапрягаемой арматуры.

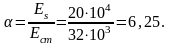
2.Статический момент площади приведенного сечения относительно нижней грани.

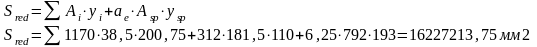(8.21)

где y-расстояние от нижней грани до центра тяжести i-ой части сечения;

3.Расстояние от нижней грани до центра тяжести приведенного сечения.

(8.22)

4.Момент инерции приведенного сечения относительно оси, проходящей через центр тяжести сечения.

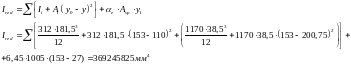
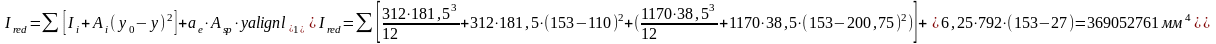
5.Момент сопротивления приведенного сечения относительно нижней его грани.

(8.23)

6. Момент сопротивления приведенного сечения с учетом неупругих деформаций растянутого бетона.

(8.24)

где =1,75 для тавровых сечений с полкой в сжатой зоне.

8.6 Расчет по образованию трещин

Расчет трещиностойкости сечений, нормальных к продольной оси для изгибаемых элементов следует производить из следующего условия:

М_sd,k ≤ M_сr, (8.25)

Где М_sd,n – изгибающий момент от нормативной нагрузки,

М_сr – изгибающий момент, воспринимаемый сечением, нормальным к продольной оси элемента при образовании трещин (усилие трещинообразования).

Усилие трещинообразования допускается определять по упрощенной зависимости как для бетонного сечения по формуле:

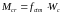, (8.26)

где f_ctm – средняя прочность бетона на осевое растяжение (для бетона класса С20/25 f_ctm=1,9 МПа).

W_c – момент сопротивления бетонного сечения.

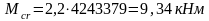
М_сr=9,34кН∙м>М_sd,к=33.9кН∙м

Условие не соблюдается, следовательно, производим расчет по раскрытию трещин.