Вопрос 30.

Плоскость общего положения

Плоскость, которая занимает произвольное положение по отношению к плоскости проекций (углы наклона этой плоскости к плоскостям проекций - произвольные, но отличные от 0° и 90°) называется плоскостью общего положения (рис. 2.12.а).

На комплексном чертеже следы плоскости общего положения составляют с осью проекций также произвольные углы.

Рассмотрим изображение на комплексном чертеже и свойства плоскостей частного положения: плоскости, перпендикулярные и параллельные плоскостям проекций.

Вопрос 31.

Плоскости частного положения - это плоскости, параллельные или перпендикулярные к плоскостям проекций.

Плоскости частного положения параллельны или перпендикулярны плоскостям проекций.

Плоскостью частного положения называется плоскость, параллельная или перпендикулярная по отношению к одной из плоскостей проекций. Плоскости частного положения подразделяют на проецирующие и плоскости уровня.

Плоскостью частного положения будем называть плоскости, которые параллельны или перпендикулярны хотя бы одной из плоскостей проекций. В системе трех плоскостей проекций они делятся на две группы.

Для плоскостей частного положения соответствующие прямые уровня одновременно являются и проецирующими. Например, у горизонтально-проекцирующей плоскости ее фронтали одновременно являются и горизонтально-проецирующими прямыми.

К плоскостям частного положения относятся проектирующие плоскости, они перпендикулярны одной или двум плоскостям проекций.

Прямые и плоскости частного положения разделяются на проецирующие прямые и плоскости, перпендикулярные плоскости проекций, и на прямые и плоскости уровня, параллельные плоскости проекций. Нетрудно видеть, что каждая проецирующая прямая является вместе с тем и прямой уровня, а каждая плоскость уровня - и проецирующей плоскостью.

Рассмотрим применение способа плоскостей частного положения на двух примерах.

Какие плоскости называют плоскостями общего и частного положения.

Если секущая плоскость - плоскость частного положения, то задача упрощается, так как одна проекция линии пересечения плоскости с кривой поверхностью уже имеется и совпадает со следом секущей плоскости.

Если секущая плоскость - плоскость частного положения, то задача упрощается, так 1ЩграддОя проекция линии пересечения плоскости с кривой поверхностью уже имеется и совпадает со следом секущей плоскости.

Точка и прямая в плоскостях частного положения, упро - в пл скости щается, как будет показано ниже.

Задание на чертеже прямых и плоскостей частного положения значительно упрощает решение задач и делает его выполнимым при помощи простых замеров или простейших графических построений.

Пример:

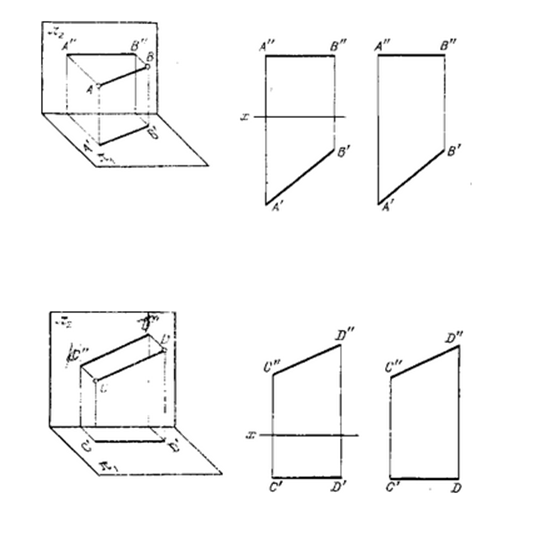
Вопрос 32.

Принадлежность точки и прямой к плоскости

ПРИНАДЛЕЖНОСТЬ ПРЯМОЙ ПЛОСКОСТИ

Сформулируем условие принадлежности прямой плоскости как аксиомы:

Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.

Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.

Точка принадлежит плоскости, если она принадлежит какой-нибудь прямой, лежащей в этой плоскости.

Из элементарной геометрии известно, что прямая принадлежит плоскости, если:

oна проходит через две точки, принадлежащие плоскости;

oна проходит через 1 точку, принадлежащую плоскости, и параллельна прямой, лежащей в плоскости.