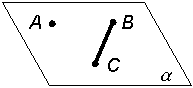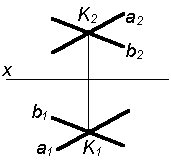Вопрос 24.

Проекции прямого угла

Любой линейный угол (острый, тупой, прямой) проецируется на плоскость проекций в истинную величину, если его стороны параллельны этой плоскости. При этом вторая проекция угла вырождается в прямую линию, перпендикулярную линиям связи.

Кроме того, прямой угол проецируется в истинную величину еще и тогда, когда только одна из его сторон параллельна плоскости проекций.

Теорема 1.

Если одна сторона прямого угла параллельна плоскости проекций, а другая является прямой общего положения, то прямой угол проецируется на эту плоскость проекций без искажения, т. е. в прямой же угол.

Теорема 2. Если прямая перпендикулярна к плоскости в пространстве, то на комплексном чертеже горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция перпендикулярна к фронтальной проекции фронтали, принадлежащим этой плоскости.

Вопрос 25.

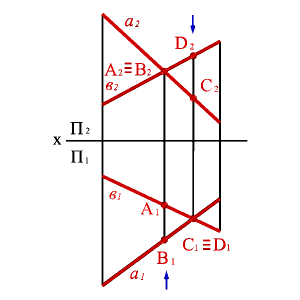
какие линии называются скрещивающимися:

Это те линии которые не параллельны и не пересекаются и не лежат в одной плоскости

Вопрос 26.

Какие точки называются конкурирующими?

Две точки, лежащие на проецирующей прямой, называются конкурирующими. С помощью конкурирующих точек можно определять взаимную видимость геометрических фигур на эпюре. Конкурирующими точками называются такие точки пространства, у которых совпадают какие-либо две одноименные проекции.

Вопрос 27.

При определении видимости ребер многогранника на двух скрещивающихся ребрах выбирается и обозначается пара конкурирующих точек. Затем строятся их вторые проекции, по которым определяется, которая из двух точек наиболее удалена от плоскости проекций. Эта точка, а следовательно и ребро, на котором лежит эта точка, будут видимы на первой плоскости проекций. Видимость определяется по конкурирующим точкам.

Вопрос 28.

.Способы задания плоскости в пространстве

Способ задания	Наглядное изображение	Комплексный чертеж
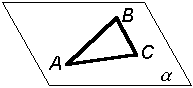
а) тремя точками, не лежащими на одной прямой

б) прямой и точкой вне данной прямой
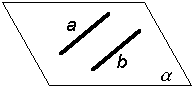
в) двумя параллельными прямыми
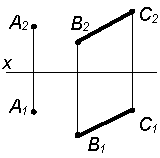
г) плоской фигурой
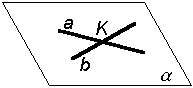
д) двумя пересекаю- щимися прямыми
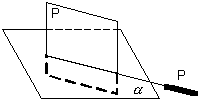
е) следом: Р  

Вопрос 29.

№29СЛЕДЫ ПЛОСКОСТИ

Взаимное расположение прямой и плоскости

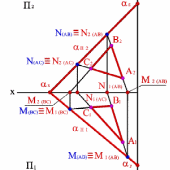
Следом плоскости называется линия пересечения плоскости с плоскостью проекций. В зависимости, от того с какой из плоскостей проекций пересекается данная плоскость, различают: горизонтальный, фронтальный и профильный следы плоскости.

Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой (как для построения любой прямой). На рисунке 52 показано нахождение следов плоскости α(АВС). Фронтальный след плоскости αП2 построен, как прямая соединяющая две точки N(АС) и N(АВ), являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости α. Горизонтальный след αП1 – прямая, проходящая через горизонтальные следы прямых ВС и АВ. Профильный след αП3 – прямая соединяющая точки (αy и αz) пересечения горизонтального и фронтального следов с осями. Точки αx, αy и αz называют точками схода следов.

Модель в ACAD Решение задачи на эпюре

Модель в bCAD

Модель в Компас

Построение эпюра из модели

а) модель б) эпюр