Вопрос 18.

Горизонтально проецирующей прямой (рис.2.З-г) называют прямую, перпендикулярную плоскости П₁. Любой отрезок этой прямой проецируется на плоскость П₂ без искажения, а на плоскость П₁ - в точку.     Фронтально проецирующей прямой (рис.2.З-д) называют прямую, перпендикулярную плоскости П₂. Любой отрезок этой прямой проецируется на плоскость П₁ без искажения, а на плоскостьП₂ - в точку.     Профильно проецирующей прямой (рис.2.З-е) называют прямую, перпенди кулярную плоскости П₃, т.е. прямую, параллельную плоскостям проекций П₁ и П₂. Любой отрезок этой прямой проецируется на плоскости П₁ и П₂ без искажения, а на плоскость П₃ - в точку. 

Вопрос 19.

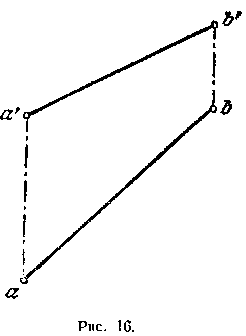
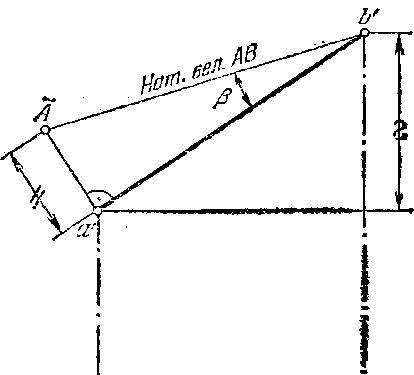
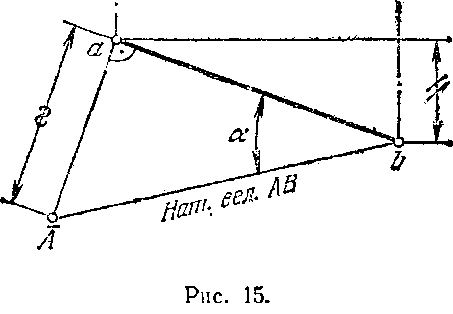
Решение. Как известно, натуральная величина отрезка может быть определена как величина гипотенузы прямоугольного треугольника, одним катетом которого является проекция отрезка на какой-либо плоскости проекций, а другим — разность расстояний концов отрезка до этой же плоскости. Если одним из катетов является горизонт, проекция, то угол между гипотенузой н этим катетом равен углу наклона (а) прямой к горизонт, плоскости проекций. Угол наклона (Р) этой же прямой к фронт, пл. проекций определяется из треугольника, в котором в качестве первого катета взята фронт, проекция отрезка, а второй катет определен по разноетн расстояний концов отрезка до фронт, пл. проекций.

Для определения натуральной величины отрезка АВ и углов а н Р на рис. 15 построены прямоугольные треугольники ЬаА и Ь'а'А. В треугольнике ЬаА катет аА равен разности расстояний точек А и В до горизонт, пл. проекций. В треугольнике Ь'а'А катет а!А равен разности расстояний точек А и В до фронт, пл. проекций.

Вопрос 20.

Угол наклона прямой к плоскости - есть угол между прямой и её проекцией на эту плоскость.

Для графического определения на эпюре Монжа действительной (натуральной) величины отрезка достаточно построить прямоугольный треугольник, взяв за один его катет горизонтальную (фронтальную, профильную) проекцию отрезка, а за другой катет - разность удаления концов отрезка от горизонтальной (фронтальной, профильной) плоскости проекций. Тогда гипотенуза треугольника будет равна натуральной величине отрезка, а угол между гипотенузой и проекцией будет равен углу наклона прямой к этой плоскости.

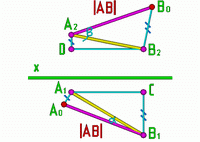
Для определения угла наклона прямой к горизонтальной плоскости (угла  ), построения выполняют на базе горизонтальной проекции.

Для определения угла наклона прямой к фронтальной плоскости (угла  ), построения выполняют на базе фронтальной проекции.

Вопрос 21.

Следы прямой их определение

Следом прямой линии называется точка в которой прямая пересекается с плоскостью проекций (так как след - точка, принадлежащая одной из плоскостей проекций, то одна из её координат должна быть равна нулю).

Горизонтальный след - М (zM=0)-точка пересечения прямой с горизонтальной плоскостью проекций.

Фронтальный след - N (yN=0)- точка пересечения прямой с фронтальной плоскостью проекций.

Профильный след - Т (xТ=0)- точка пересечения прямой с профильной плоскостью проекций.

Следы прямой являются точками частного положения.

Следы прямой являются точками, одновременно принадлежащими как плоскости проекций, так и прямо. Следы прямой, являются точками, в которых прямая переходит из одного октанта в другой, позволяют отмечать её видимость. Видимой частью прямой будет та, которая расположена в пределах первого октанта