Вопрос 15.

Прямая общего положения

По расположению относительно плоскостей проекций бывает прямая общего положения и частного.

Прямая общего положения - это прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций.

Отрезок [AB] определяющий прямую l занимает произвольное положение по отношению к плоскостям проекций (углы наклона прямой l к плоскостям H, V, и W произвольные - отличные от 0 и 90 град.). Такая прямая есть прямая общего положения.

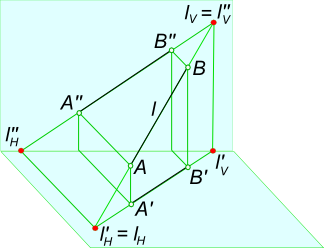
Прямая общего положения

Прямая общего положения пересекает все три плоскости проекций. Точку пересечения (встречи) прямой с плоскостью проекции называют следом прямой.

Прямая общего положения

В зависимости от того, с какой плоскостью проекции происходит встреча прямой l, следы обозначают и называют: l _H - горизонтальный след прямой l; l _V - фронтальный след прямой l; l _W - профильный след прямой l.

Вопрос 16.

Прямая частного положения

Прямые частного положения подразделяются на прямые уровня и проецирующие .Прямые частного положения перпендикулярны или параллельны плоскостям проекций. Прямой частного положения называется прямая, которая параллельна хотя бы одной из плоскостей проекций. Отрезок прямой частного положения проецируется в натуральную величину на плоскость, которой эта прямая параллельна. К прямым частного положения относятся прямые, параллельные одной или двум плоскостям проекции.

Прямые частного положения     К прямым частного положения относятся прямые, параллельные одной или двум плоскостям проекций.     Любую линию (прямую или кривую), параллельную плоскости проекций, называют линией уровня. В инженерной графике различают три основные линии уровня: горизонталь, фронталь и профильную линии. 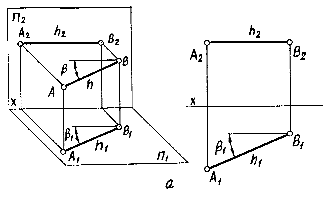  Рис. 2.3-а

   Горизонталью называют любую линию, параллельную горизонтальной плоскости проекций (рис.2.З-а). Фронтальная проекция горизонтали всегда перпендикулярна линиям связи. Любой отрезок горизонтали на горизонтальную плоскость проекций проецируется в истинную величину. В истинную величину проецируется на эту плоскость и угол наклона горизонтали (прямой) к фронтальной плоскости проекций. В качестве примера на рис.2.З-а дано наглядное изображение и комплексный чертеж горизонтали h, наклоненной к плоскости П₂ под углом 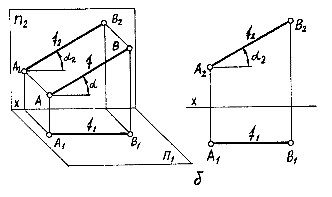.   Рис. 2.3-б

   Фронталью называют линию, параллельную фронтальной плоскости проекций (рис.2.3-б). Горизонтальная проекция фронтали всегда перпендикулярна линиям связи. Любой отрезок фронтали на фронтальную плоскость проекций проецируется в истинную величину. В истинную величину проецируется на эту плоскость и угол наклона фронтали (прямой) к горизонтальной плоскости проекций (угол ).   Рис. 2.3-в

   Профильной линией называют линию, параллельную профильной плоскости проекций (рис.2.З-в). Горизонтальная и фронтальная проекции профильной линии параллельны линиям связи этих проекций. Любой отрезок профильной линии (прямой) проецируется на профильную плоскость в истинную величину. На эту же плоскость проецируются в истинную величину и углы наклона профильной прямой к плоскостям проекций П₁ и П₂. При задании профильной прямой на комплексном чертеже нужно обязательно указать две точки этой прямой.  Вопрос17.    Прямые уровня, параллельные двум плоскостям проекций, будут перпендикулярны третьей плоскости проекций. Такие прямые называют проецирующими. Различают три основные проецирующие прямые: горизонтально, фронтально и профильно проецирующие прямые.   Рис. 2.3-г   Рис. 2.3-д   Рис. 2.3-е