Вопрос 12.

Показатели отношений к, m и n будут называться в дальнейшем коэффициентами искажения. Таким образом, коэффициентом искажения по аксонометрической оси называется отношение длины проекции отрезка к длине самого отрезка, взятого на оси координат.

В зависимости от направления проецирования и положения осей координат относительно плоскости аксонометрических проекций коэффициенты искажения могут быть больше, меньше или равны единице. А это значит, что коэффициенты искажения при косоугольном проецировании могут изменяться в пределах от нуля до бесконечности.

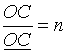
В зависимости от направления проецирования аксонометрические проекции делятся на косоугольные и прямоугольные. По признаку соответствия коэффициентов искажения между собой аксонометрические проекции можно разделить на изометрические, диметрические и триметрические. Если в аксонометрии все три коэффициента будут равны – k = m = n, то получается изометрическая (isos – одинаковый) проекция, т. е. проекция одинаковых коэффициентов по всем трем осям.

Если равны между собой будут два из коэффициентов искажения, а третий не равен им, то образуется диметрическая (di – двойной) проекция или аксонометрия одинаковых коэффициентов искажения по двум осям. В диметрии могут быть случаи когда  ,   или  .

Если же все три коэффициента будут различны –  , то получается триметрическая (treis – три) проекция, т. е. проекция различных коэффициентов искажения по всем трем осям.

Вопрос 13.

1) изометрические, т.е. одинакового измерения (оси z', х' и у' наклонены одинаково; следовательно, уменьшение размеров по направлению всех трех осей одинаковое); 2) диметрические, т. е. двойного измерения (две оси координат имеют один и тот же наклон, а третья - другой; следовательно, уменьшение размеров по этим двум осям будет одно и то же, а по третьей оси - другое); 3) триметрические, т.е. тройного измерения (все оси имеют разный наклон; следовательно, уменьшение размеров по направлению всех трех осей разное).

Вопрос 14.

Задание и изображение на чертеже. Прямая линия в пространстве определяется положением двух ее точек, например А и B. Значит, достаточно выполнить комплексный чертеж этих точек, а затем соединить одноименные проекции точек прямыми линиями, получим соответственно горизонтальную и фронтальную проекции прямой. Прямая общего положения называется прямая не параллельная ни одной из плоскостей проекций. Прямая, параллельная или перпендикулярная одной из плоскостей проекций, называется прямой частного положения.

Прямая линия - это простейший представитель семейства линий. На комплексном чертеже прямая линия может быть задана непосредственно своими проекциями, проекциями двух точек принадлежащих прямой или следами. При ортогональном проецировании на плоскость, не перпендикулярную ей, прямая проецируется в прямую линию. Чтобы спроецировать отрезок прямой линии АВ на плоскость, из крайних точек отрезка опускают перпендикуляры на плоскость проекций и полученные проекции точек А1 и В 1 соединяют прямой которая и будет проекцией данного отрезка.