Вопрос 66.

Разверткой называется плоская фигура, полученная совмещением поверхности тела с плоскостью. Для построения многогранной поверхности (см. также здесь) необходимо совместить с плоскостью все ее грани (практика в Coreldraw здесь). Для построения развертки поверхности в общем случае надо в нее вписать многогранную поверхность и совместить с плоскостью. Поверхности, которые разворачиваются на плоскость без разрывов и складок, называются развертываемыми. К ним относятся линейчатые поверхности, у которых образующие параллельны или пересекаются (цилиндры, торсы, конусы). Остальные поверхности неразвертываемые. Развертки обладают многими одинаковыми свойствами самих поверхностей: равенством длинами прямых, равенством углов между линиями, параллельностью прямых. Развертки простых фигур можно строить и математически. Для цилиндра - это прямоугольник с длиной S = 2R; для конуса - сектор с углом при вершине = 2 R / l (l - длина образующей). Однако чаще это сложные поверхности с вырезами и срезами на них, развертки которых возможно только использую графические приемы. Основной метод графического построения разверток - это аппроксимация заданной поверхности в виде многогранной поверхности. Часто вписывают многогранник с гранями в виде треугольников. Данный способ называется способом триангуляции. Самой трудоемкой частью при построении разверток является определение натуральной величины граней вписываемого в поверхность многогранника. Имеется ряд способов и приемов, сокращающих эту работу и облегчающих построение разверток. К ним относятся способ треугольников, способ нормального сечения и способ раскатки, которые, в свою очередь, используют, методы определения натуральной величины граней методами замены плоскостей проекций (ортогонального проецирования по нормали к плоскости грани) или вращения вокруг проецирующих осей. Данные преобразования с использования приемов сдвига возможны и в системе "СG - Вектор".

Вопрос 67.

развёртка поверхности называется фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. 

Вопрос 68.

Для механизации и автоматизации конструкторско-графических работ все более широкое применение находят графические автоматы различных типов. Одни из них позволяют получать и размножать чертежи непосредственно на бумаге (графопостроители), другие – получить их изображение на экране (графические дисплеи). Автоматизированные графические устройства могут работать в индивидуальном режиме с соответствующей подготовкой для этого исходных данных и в режиме связи с ЭВМ, когда проектировщик может выбрать оптимальные варианты решения задач. Графические автоматы находят широкое применение в системах автоматизированного проектирования.

Вопрос 69.

Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В пространстве необходимо уже 3 координаты 

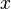•  — расстояние от точки P до плоскости yz

•  — расстояние от точки P до плоскости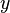 xz

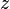•  — расстояние от точки P до плоскости xy