Вопрос 57.

Многогранник называется правильным, если все его грани — равные правильные многоугольники, а все многогранные углы имеют одинаковое число граней. Все ребра правильного многогранника — равные отрезки, все плоские углы правильного многогранника также равны. Существует пять различных правильных многогранников (выпуклых): правильный четырехгранник (правильный тетраэдр), правильный шестигранник (куб), правильный восьмигранник (правильный октаэдр), правильный двенадцатигранник (правильный додекаэдр), правильный двадцатигранник (правильный икосаэдр).

Обозначения:  а — длина ребра;  V — объем; S_бок — площадь боковой поверхности; S_полн — площадь полной поверхности; R — радиус описанной сферы;  r — радиус вписанной сферы;  h — высота.

Вопрос 58.

сечением многогранника называют многоугольник, вершины которого лежат на ребрах многогранника, а стороны – на его гранях.

Чтобы построить сечение многогранника плоскостью, необходимо:

1) провести прямые через пары точек, лежащих в одной плоскости.

2) найти прямые, по которым пересекаются плоскости сечения и грани многогранника. Для этого нужно найти точки пересечения прямой, принадлежащей плоскости сечения, с прямой, лежащей в одной из граней.

Вопрос 59.

НАКЛОННЫЕ СЕЧЕНИЯ ГРАННЫХ ТЕЛ

   Построение линии пересечения плоскости с гранным геометрическим телом сводится к построению линии пересечения двух плоскостей и построению точки встречи прямой и плоскости.     На рис. 8.1. рассмотрен пример построения линии пересечения плоскости с правильной шестиугольной пирамидой. Так как секущая плоскость перпендикулярна фронтальной плоскости проекций, то фронтальная проекция линии пересечения на чертеже уже имеется. Она совпадает с фронтальной проекцией секущей плоскости. Горизонтальную проекцию линии пересечения строим по точкам.     Секущая плоскость пересекает ребра пирамиды в точках M, N, О, P, T, а основание пирамиды - по прямой KL. Проведя соответствующие линии связи, можно легко построить горизонтальные проекции точек. Соединив их, получим горизонтальную проекцию линии пересечения. 

 Рис. 8.1.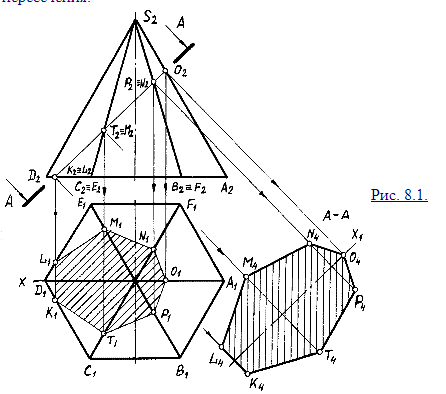

   При решении практических задач очень часто необходимо знать натуральную величину сечения, которую построим методом проецирования на дополнительную плоскость проекций. Для этого введем дополнительную плоскость П₄, параллельную секущей плоскости. Так как секущая плоскость перпендикулярна фронтальной плоскости проекций П₂, то и П₄ П₄.     Ось х проведем через горизонтальную проекцию вершины пирамиды S₁, а новая ось x₁ будет параллельна фронтальной проекции секущей плоскости. От фронтальных проекций точек K, L, M, N, 0, P, T проводим линии связи перпендикулярно новой оси x₁. Далее от оси x₁вдоль линий связи отложим координаты Y соответствующих точек, которые определим на горизонтальной плоскости проекций. Получим проекции K₄, L₄, M₄, NS₄, O₄, P₄, T₄ точек K, L, M, N, 0, P, T на плоскость П₄. Соединив их, получим натуральную величину сечения (более подробно метод проецирования на дополнительную плоскость рассмотрен в главе 5).     Здесь следует заметить, что линии связи отсекают на оси x₁ отрезки равные по величине отрезкам между проекциями соответствующих точек, расположенных на фронтальной проекции секущей плоскости.     Построенное наклонное сечение необходимо заштриховать. Линии штриховки располагают или под углом 45° к горизонтальным линиям чертежа, или под углом 45° к оси x₁. Обозначают наклонные сечения аналогично разрезам, т.е. на продолжении секущей плоскости проводят два штриха толщиной в 1,5 раза толще линий контура, длиной 10-12 мм, а перпендикулярно к штрихам на расстоянии 2-3 мм от их наружных концов проводят стрелки, указывающие направление взгляда. С наружных сторон стрелок наносятся вертикально буквы русского алфавита, а над сечением выполняется надпись по типу "А-А" (рис. 8.1).