Вопрос 54.

Кинематический способ.

Поверхность рассматривается как совокупность всех последовательных положений некоторой линии – образующей, перемещающейся в пространстве по определенному закону. Линия, которую пересекают все образующие поверхности, называется направляющей.

Упорядоченное множество линий, принадлежащих поверхности, называется ее каркасом. Обычно в качестве линий каркаса используют семейство образующих или семейство направляющих.

Вопрос 55.

Кривые поверхности широко применяются в различных областях науки и техники при создании очертаний различных технических форм или как объекты инженерных исследований. Существуют три способа задания кривых поверхностей:

1. Аналитический - при помощи уравнений;

2. При помощи каркаса;

3. Кинематический, т. е. перемещением линий в пространстве.

Вопрос 56.

Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой). Например, если прямая пересекает ось вращения, то при её вращении получится коническаяповерхность, если параллельна оси — цилиндрическая, если скрещивается с осью — однополостный гиперболоид вращения. Одна и та же поверхность может быть получена вращением самых разнообразных кривых.

Является объектом изучения в математическом анализе, аналитической и начертательной геометрии^[

Линии пересечения поверхностей вращения обычно строят при помощи вспомогательных параллельных плоскостей или вспомогательных концентрических сфер в зависимости от взаимного расположения данных поверхностей и положения их по отношению к плоскостям проекций. Построение линий пересечения поверхностей вращения при помощи параллельных вспомогательных плоскостей. Данные поверхности пересекают несколькими параллельными плоскостями, каждая из которых пересекает поверхности тел по некоторым линиям, которые, находясь в одной плоскости, пересекутся; точки пересечения этих линии явятся общими для данных поверхностей вращения и, следовательно, принадлежат их линиям пересечения.

Найдя достаточное количество таких точек, их соединяют и получают линию пересечения данных поверхностей.
Выбор положения вспомогательной плоскости необходимо связывать с тем, чтобы плоскость пересекала каждую поверхность по простой и удобной для выполнения линии, т. е. по прямой или по окружности. Например, прямой круговой цилиндр - по образующим или по окружностям (параллельно основанию); пр.чмой круговой конус - по параллелям или по образующим; тела вращения (например, кольцо) - по окружностям (перпендикулярно оси вращения); шар - по параллелям.

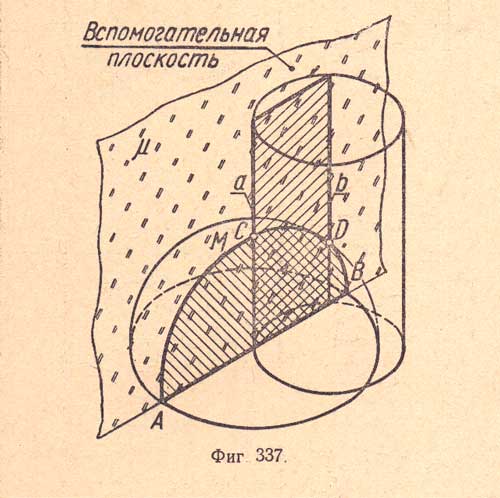
На (фиг.337) показано применение вспомогательной плоскости, когда пересекаются поверхности шара и прямого кругового цилиндра.

Эти тела рассечены вспомогательной плоскостью μ, параллельной осям вращения шара и цилиндра. Шар рассечен по меридиану - окружности (в данном случае дуге АМВ), а цилиндр - по образующим - прямым а и Ь. Полученные в результате сечения прямые и дуга пересеклись в точках С и D. Эти точки принадлежат линии взаимного пересечения данных поверхностей.

Разберем несколько примеров построения линий пересечения при помощи параллельных секущих вспомогательных плоскостей.