Вопрос 49.

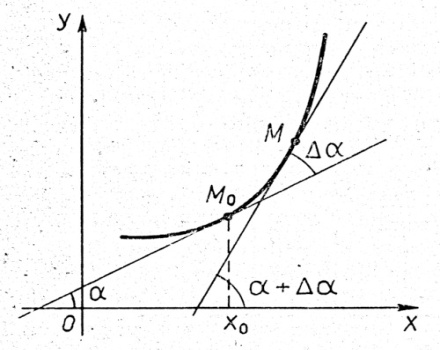
Рассмотрим плоскую линию, определяемую уравнением   y = ƒ(x). Проведём касательную к этой линии в точке   M₀(x₀, y₀); обозначим через   α   угол, образованный касательной с осью   Ox. Пусть касательная в точке   M   образует с осью   Ox   угол   α + Δα. Угол   Δα   между касательными в указанных точках называют углом смежности. Можно сказать, что при переходе из точки   M₀   в точку   M   данной линии касательная к ней повернулась на угол   Δα, которому будем приписывать соответствующий знак в зависимости от направления поворота. Средней кривизной   <k>   дуги   данной линии называется абсолютное значение отношения угла смежности Δα   к длине   Δℓ   дуги  :   <k> = |Δα/Δℓ|.

Кривизной линии в данной точке   M₀   называется предел средней кривизны дуги   при M → M₀: . Отметим, что для прямой   k = 0, а для окружности радиуса   R   кривизна   k = 1/R. Кривизна линии, заданной уравнением   y = ƒ(x), в точке   M(x, y) вычисляется по формуле: k = |y″|/√(1 + y′²)³ Если линия задана параметрическими уравнениями   x = x(t),   y = y(t), то формула принимает вид: k = |x′·y″ − x″·y′|/√(x′² + y′²)³ Кривизна линии, заданной уравнением   ϱ = ϱ(φ)   в полярных координатах, вычисляется по формуле: k = |ϱ² + 2·ϱ′² − ϱ·ϱ″|/√(ϱ′² + ϱ²)³

Пример 1 Найти кривизну косинусоиды   y = cos x   в точке   M(0, 1).

Поскольку   y′ = −sin x,   y″ = −cos x, кривизна косинусоиды в её произвольной точке определяется формулой k = |cos x|/√(1 + sin²x)³ При   x = 0   получаем   k = 1/√1³ = 1.

Пример 2 Найти кривизну линии, заданной в полярных координатах ϱ = a·(1 + cos φ) = 2·a·cos²(½ φ)

Данное уравнение определяет кардиоиду. Кардиоида — линия, описываемая точкой   M   окружности радиуса   r, катящейся по окружности с таким же радиусом.

Вопрос 50.

ПРОСТРАНСТВЕННЫЕ КРИВЫЕ ЛИНИИ:

Пространственные кривые линии в начертательной геометрии обычно рассматриваются как результат пересечения поверхностей или траекторию движения точки.

Пространственную, так же как и плоскую, кривую линию на чертеже задают последовательным рядом точек.

Классическим примером пространственных кривых линий являются цилиндрическая и коническая винтовые линии.

Цилиндрическая винтовая линия.

Такую линию в пространстве описывает точка, которая движется по какой-либо образующей прямого кругового цилиндра, вращающегося вокруг своей оси так, что путь проходимый точкой по образующей пропорционален углу поворота цилиндра

Смещение точки вдоль образующей за один оборот называется шагом цилиндрической винтовой линии. Различают правую и левую винтовые линии.

Коническая винтовая линия.

Такую линию описывает точка, которая движется по какой-либо образующей прямого кругового конуса, вращающегося вокруг своей оси так, что путь пройденный точкой по образующей все время равен углу поворота конуса.

Проекция на ось конуса смещения точки вдоль образующей за один оборот называется шагом конической винтовой линии. Горизонтальной проекцией конической винтовой линии является спираль Архимеда - одна из замечательных плоских кривых линий.