
- •Ответы на зачет по Начертательной геометрии.
- •Вопрос 1
- •Вопрос 2.
- •Вопрос 3.
- •Вопрос 4.
- •Вопрос 5.
- •Вопрос 6.
- •Вопрос 7.
- •Вопрос 8.
- •Вопрос 9.
- •Вопрос 10.
- •Вопрос 11.
- •Вопрос 12.
- •Вопрос 13.
- •Вопрос 14.
- •Вопрос 15.
- •Вопрос 16.
- •Вопрос 18.
- •Вопрос 19.
- •Вопрос 20.
- •Вопрос 21.
- •Вопрос 22.
- •Вопрос 23.
- •Вопрос 24.
- •Вопрос 25.
- •Вопрос 26.
- •Вопрос 27.
- •Вопрос 28.
- •Вопрос 29.
- •Вопрос 30.
- •Вопрос 31.
- •Вопрос 32.
- •Вопрос 33.
- •Вопрос 34.
- •Вопрос 35.
- •Вопрос 36.
- •Вопрос 38.
- •Вопрос 39.
- •Вопрос 40.
- •Вопрос 41.
- •1. Одним из способов преобразования комплексного чертежа привести обе заданные геометрические фигуры (или одну из них) в положение, перпендикулярное какой-либо плоскости проекций.
- •2. Построить проекцию искомого отрезка на эту плоскость.
- •Вопрос 42.
- •Вопрос 43.
- •Вопрос 44.
- •Вращение точки
- •Вопрос 45.
- •Вопрос 46.
- •Вопрос 47.
- •Вопрос 48.
- •Вопрос 49.
- •Вопрос 50.
- •Вопрос 51.
- •Вопрос 52.
- •Вопрос 53.
- •Вопрос 54.
- •Вопрос 55.
- •Вопрос 56.
- •Вопрос 57.
- •Вопрос 58.
- •Вопрос 59.
- •Вопрос 60.
- •Вопрос 61.
- •Вопрос 62.
- •Вопрос 63.
- •Вопрос 64.
- •Вопрос 65.
- •Вопрос 66.
- •Вопрос 67.
- •Вопрос 68.
- •Вопрос 69.
- •Вопрос 70.
Вопрос 33.
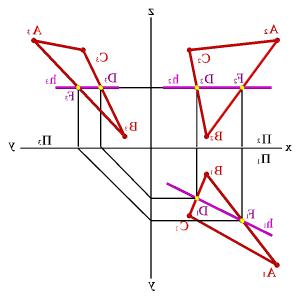 1.
Горизонтали h - прямые, лежащие в данной
плоскости и параллельные горизонтальной
плоскости проекций
1.
Горизонтали h - прямые, лежащие в данной
плоскости и параллельные горизонтальной
плоскости проекций
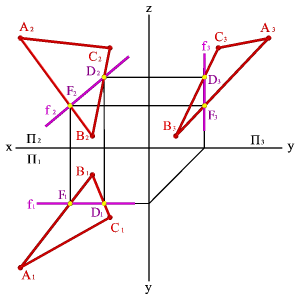 2.
Фронтали f - прямые, расположенные в
плоскости и параллельные фронтальной
плоскости проекций
2.
Фронтали f - прямые, расположенные в
плоскости и параллельные фронтальной
плоскости проекций
 3.
Профильные прямые р - прямые, которые
находятся в данной плоскости и параллельны
профильной плоскости проекций.
3.
Профильные прямые р - прямые, которые
находятся в данной плоскости и параллельны
профильной плоскости проекций.
4. Прямые, принадлежащие плоскости и образующие с плоскостью проекций наибольший угол называются линиями наибольшего наклона данной плоскости к плоскости проекций.
5. Линия наибольшего наклона к горизонтальной плоскости проекций называется линией ската.
Вопрос 34.
Плоскости, параллельные плоскостям проекций
(плоскости уровня)
1. Горизонтальная плоскость γ || π1.
Плоскость γ, параллельная плоскости π1, называется горизонтальной (рис. 2.15).
Любая фигура, расположенная в такой плоскости, проецируется на горизонтальную плоскость проекций в натуральную величину (Δ А1В1С1 = ΔАВС, рис. 17). Фронтальный след этой плоскости параллелен оси Х (f0g | | Х).
2. Фронтальная плоскость δ | | π2.
Плоскость δ, параллельная плоскости π2, называется фронтальной.
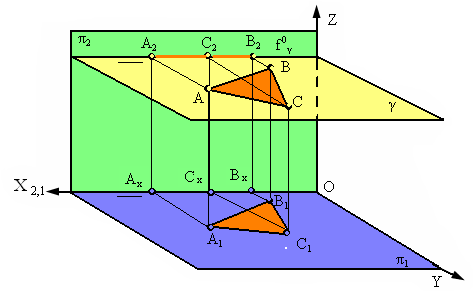
Рис. 2.15. Плоскость, параллельная горизонтальной плоскости проекций
Любая фигура, расположенная в такой плоскости, проецируется на фронтальную плоскость проекций без искажения, т. е. в натуральную величину.
Горизонтальный след фронтальной плоскости параллелен оси Х.
Примечание. Плоскость, параллельная одной из плоскостей проекций, является частным случаем проецирующих плоскостей.
Вопрос 35.
Поверхности вращения.
Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой). Например, если прямая пересекает ось вращения, то при её вращении получится коническая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — однополостный гиперболоид вращения. Одна и та же поверхность может быть получена вращением самых разнообразных кривых.
Сфера (получается вращением окружности вокруг оси, лежащей в той же плоскости и проходящей через её центр).
Тор (получается вращением окружности вокруг не пересекающей её оси, лежащей в той же плоскости).
Эллипсоид вращения ― эллипсоид, длины двух полуосей которого совпадают. Может быть получен вращением эллипса вокруг одной из его осей.
Параболоид вращения ― эллиптический параболоид, полученный вращением параболы вокруг своей оси.
Конус получается вращением прямой вокруг другой прямой, пересекающей первую.
Круговая цилиндрическая поверхность
Катеноид
Вопрос 36.
В пространстве две плоскости могут быть параллельными, совпадающими и пересекающимися. Линия пересечения двух плоскостей – это прямая, для построения которой нужно определить две точки, общие для этих плоскостей. Постройте две непараллельные плоскости, которые в то же время не должны совпадать между собой, и назовите их a и b
2
Пусть плоскость b задана будет треугольником (АВС). Для решения данной задачи вам необходимо найти две точки, которые были бы одновременно общими для двух плоскостей, и провести через них прямую линию.
3
Плоскость b может быть представлена тремя прямыми линиями: АВ, ВС и АС. Точку пересечения прямой АВ с плоскостью a назовите точкой D.
4
Найдите точку пересечения плоскости a с прямой АС и назовите ее точкой F. Отрезок DF и будет представлять собой линию пресечения двух заданных плоскостей.
5
Частный случай пересекающихся плоскостей – взаимно перпендикулярные плоскости. Две пересекающиеся плоскости будут перпендикулярными в том случае, если третья плоскость (назовем ее g) будет перпендикулярна прямой пересечения заданных плоскостей (a и b). Другими словами, плоскость a будет перпендикулярна плоскости b, если плоскость g перпендикулярна прямой с (являющейся линией пересечения плоскостей a и b), при этом прямая а принадлежать будет плоскости a, а прямая b – плоскости b.
6
Первый признак перпендикулярности двух плоскостей: если плоскости b принадлежит прямая b, которая в свою очередь перпендикулярна плоскости a, то плоскости a и b перпендикулярны между собой.
7
Второй признак перпендикулярности рассматриваемых плоскостей: если плоскость a перпендикулярна плоскости bи к плоскости a подведен перпендикуляр, который имеет общую с плоскостью bточку, то данный перпендикуляр лежит в плоскости b. Прямая, проходящая между перпендикулярными плоскостями (в этом случае прямая с), и будет линией пересечения заданных плоскостей. Вопрос 37.
Как определяется параллельность линии заданной плоскостьи
Плоскости, перпендикулярные плоскостям проекций (проецирующие плоскости)
1. Горизонтально-проецирующая плоскость α ┴ π1.
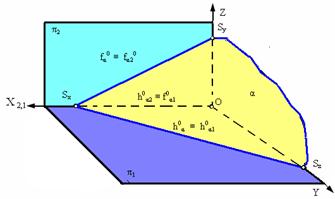
Плоскость α, перпендикулярная горизонтальной плоскости проекции π1, называется горизонтально проецирующей (рис. 2.13).
Основным свойством горизонтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π1 в прямую линию (горизонтальный след плоскости h0α).
Угол b, который составляет горизонтальный след плоскости h0a c координатной осью Х, равен углу наклона плоскости a к плоскости проекций p2. Фронтальный след такой плоскости перпендикулярен оси Х (f0a ┴ X).
2. Фронтально-проецирующая плоскость β ┴ π2.
Плоскость b перпендикулярная фронтальной плоскости проекций π2 называется фронтально проецирующей (рис. 2.14).

а б в

г д е
ж
Рис. 2.12. Способы задания плоскости: а - тремя точками, не лежащими на одной прямой; б - прямой и точкой вне ее; в - двумя пересекающимися прямыми; г - двумя параллельными прямыми; д,е - плоской фигурой; ж - следами плоскости |
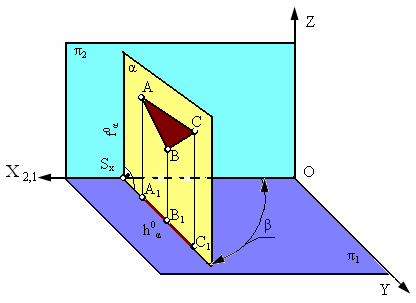
Рис. 2.13. Горизонтально-проецирующая плоскость
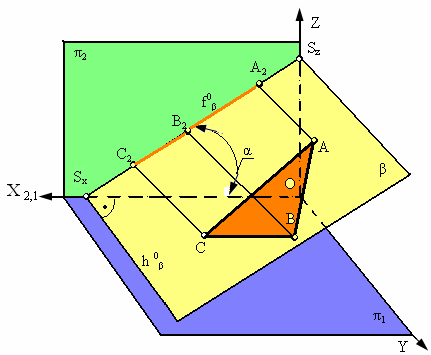
Рис. 2.14. Фронтально-проецирующая плоскость
Основным свойством фронтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π2 в прямую линию (фронтальный след плоскости f0β). Угол a, который составляет фронтальный след плоскости f0β с координатной осью Х, равен углу наклона плоскости b к плоскости проекций π1. Горизонтальный след такой плоскости перпендикулярен оси Х.
