8.14. Рівняння Пуассона і рівняння Лапласа
Виконаємо вивід цих рівнянь, які є основними рівняннями електростатики, використавши теорему Гаусса в диференціальній формі (8.30, а):
.
Підставивши
сюди
,
отримаємо:
.
Винесемо «мінус» за знак дивергенції:
.
Запишемо
замість
його еквівалент
,
а замість
–
.
Тоді:
або
. (8.36)
Рівняння (8.36) називають рівнянням Пуассона. Його частковий вигляд, коли , називають рівнянням Лапласа:
.
(8.37)
Оператор
носить назву оператора Лапласа і
позначається символом
(дельта).
Розкриємо
в декартовій системі координат. З цією
метою добуток двох множників
і
запишемо в розгорнутому вигляді й
почленно перемножимо:
Тоді рівняння Пуассона і рівняння Лапласа в декартовій системі координат відповідно запишуться:
(8.38)
(8.39)
Таким чином, рівняння Пуассона дає зв’язок між частинними похідними другого порядку від потенціалу в будь-якій точці поля.
У той же час потенціал в будь-якій точці поля залежить від усіх зарядів, що створюють поле, а не тільки від величини вільного заряду , який знаходиться в даній точці.
Виведемо вираз розв’язку рівняння Пуассона в загальному вигляді.
Припустимо,
що в об’ємі
є об’ємні (
),
поверхневі (
)
і лінійні (
)
заряди. Представимо ці заряди у вигляді
сукупностей точкових зарядів:
,
,
,
де
– елемент зарядженого об’єму,
– елемент зарядженої поверхні,
– елемент зарядженої осі.
Складова
потенціалу
в деякій точці простору, яка віддалена
від
на відстань
,
у відповідності з формулою (8.29) рівна:
.
Складові потенціалу від поверхневого і лінійного зарядів, якщо розглядати їх як «точкові», запишуться аналогічно:
і
.
Повне
значення потенціалу
визначиться як сума (інтеграл) складових
потенціалу від усіх зарядів у полі:
,
(8.40)
де , і являються функціями радіуса .
При застосуванні формули (8.40) мають на увазі, що потенціал у нескінченності рівний нулю і що заряди, які створюють поле, розподілені в обмеженій області, інакше інтеграл може виявитись розбіжним.
При інтегруванні рівняння Пуассона (або Лапласа) в його розв’язок будуть входити постійні (сталі) інтегрування. Їх визначають, виходячи з граничних умов, тобто умов, які визначають поле на межі розділу середовищ з різними електричними властивостями.
8.15. Електростатичне поле провідного тіла
У провідному тілі, яке знаходиться в електростатичному полі, завдяки явищу електростатичної індукції відбувається перерозподіл електричних зарядів.
Від’ємні заряди зміщуються на поверхню тіла, яка знаходиться зі сторони більш високого потенціалу, а додатні – в протилежну сторону (рис. 8.13).
Всі точки тіла будуть мати однаковий потенціал, тобто поверхня провідного тіла стане еквіпотенціальною. Якби між деякими точками тіла виникла різниця потенціалів, то під її дією утворився б упорядкований рух зарядів, що протирічило б поняттю електростатичного поля.
В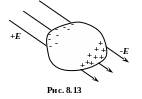
ектор
напруженості
зовнішнього поля в будь-якій точці
поверхні підходить до цієї поверхні
під прямим кутом.
Всередині провідного тіла напруженість поля рівна нулю, так як зовнішнє поле компенсується полем зарядів, що знаходяться на поверхні тіла.