8.3. Потенціальність електростатичного поля

Виведемо формулу для різниці потенціалів у полі точкового заряду в функції шляху. Для цього припустимо, що в точці (рис. 8.3) знаходиться додатний точковий заряд , який створює поле, а з точки 1 в точку 2 траєкторією 1-3-2 рухається одиничний додатний заряд . На рис. 8.3 через , , позначено відстані від точки до точок 1, 3, 2 відповідно, а напрямки напруженості й елемента шляху показані для д овільної проміжної точки 3.

Скалярний добуток двох векторів визначає елементарну роботу на шляху :

, (8.6)

де – проекція елемента шляху на напрямок радіуса .

У відповідності з формулою (8.2):

а на підставі закону Кулона (8.1):

Так як й , то і формула (8.1) прийме вигляд:

(8.7)

Враховуючи (8.6) і (8.7), вираз (8.4) для різниці потенціалів запишеться:

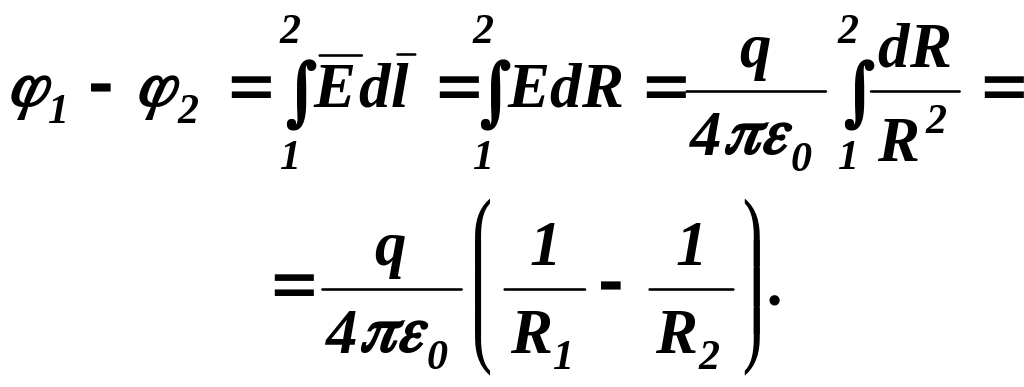(8.8)

Звідси випливає, що різниця потенціалів між початковою і кінцевою точками шляху (між точками 1 і 2) залежить тільки від розташування цих точок і не залежить від шляху, яким відбувалось переміщення з початкової точки в кінцеву.

Іншими словами,

Якби заряд переміщався замкненим шляхом 1-3-2-4-1, то початкова і кінцева точки співпали б і тоді б: . (8.9)

Таким чином, в електростатичному полі лінійний інтеграл від напруженості електричного поля вздовж будь-якого замкненого шляху рівний нулеві.

Рівність трактується ще й так:

Циркуляція вектора напруженості вздовж будь-якого замкненого контура рівна нулеві.

Поля, для яких виконуються співвідношення типу (8.9) називають потенціальними: електростатичне, гравітаційне, усталені температурні поля і т.п.

8.4. Силові та еквіпотенціальні лінії поля

Силова лінія – це уявно проведена в полі лінія, яка починається на додатно зарядженому тілі і закінчується на від’ємно зарядженому тілі, причому дотична до неї в будь-якій точці співпадає з напрямком напруженості поля в цій точці (рис. 8.4). Так як додатний і від’ємний заряди, які створюють поле, не можуть бути одночасно в одній і в тій же точці, то силові лінії електричного поля не можуть бути замкненими самими на себе лініями.

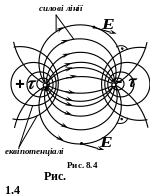
Еквіпотенціальна (рівнопотенціальна) поверхня – це сукупність точок поля, що мають один і той же потенціал.

Еквіпотенціальні лінії – це сліди перетину січної площини з еквіпотенціальними поверхнями.

Еквіпотенціальні і силові лінії перетинаються в будь-якій точці поля під прямим кутом.

На відмінність від силових ліній еквіпотенціальні лінії є замкненими самими на себе лініями.

8.5. Напруженість і градієнт потенціалу

Так як електростатичне поле є потенціальним, то між будь-якими двома точками поля існує різниця потенціалів, розділивши яку на найкоротшу відстань між цими точками в напрямку зростання потенціалу, одержимо швидкість зміни потенціалу в даному напрямку, тобто градієнт потенціалу.

Виведемо залежність між градієнтом потенціалу і напруженістю поля. З цією метою візьмемо відрізки двох еквіпотенціалей (рис. 8.5), одна з яких має потенціал , а друга – потенціал . Нехай > .

Т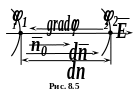 оді у відповідності з приведеним вище правилом градієнт потенціалу визначається вектором, який перпендикулярний до еквіпотенціалей і спрямований у напрямку збільшення потенціалу (від до ).

Напруженість електростатичного поля направлена від більше високого потенціалу до більш низького (від до ).

Якщо – відстань по нормалі між еквіпотенціальними поверхнями, а – вектор, який співпадає з напрямком вектора , то

,

де – одиничний вектор у напрямку вектора .

Тоді на підставі виразу (8.4):

, (8.4,а)

де – приріст потенціалу при переході від точки 1 до точки 2.

Так як вектори і співпадають за напрямком , то

і згідно з виразом (8.4, а): . Звідси модуль напруженості поля:

.

Вектор напруженості поля , отже,

. (8.10)

У відповідності з визначенням градієнта потенціалу:

. (8.11)

Співставляючи вирази (8.10) і (8.11), отримуємо:

, (8.12)

тобто напруженість у будь-якій точці поля рівна швидкості зміни потенціалу в цій же точці, взятій з протилежним знаком. Знак «–» означає, що напрямок і напрямок взаємно протилежні (рис. 8.5).

Нормаль у загальному випадку може займати загальне положення, тобто не співпадати з напрямком ні однієї координатної осі, і, тому, градієнт потенціалу в загальному випадку можна представити у вигляді суми трьох проекцій на координатні осі. Наприклад, в декартовій системі координат:

, (8.13)

де – швидкість зміни потенціалу в напрямку осі х;

– числове значення (модуль) цієї швидкості;

– одиничні орти осей х, у, z.

Виразимо вектор напруженості через свої проекції:

, (8.14)

і, співставляючи вирази (8.13) та (8.14), на підставі рівності (8.12) одержимо:

. (8.15)

Два вектори рівні тільки тоді, коли взаємно рівні їх відповідні проекції, тобто:

; ; . (8.16)

Звідси випливає, що проекція напруженості електростатичного поля рівна проекції швидкості зміни потенціалу уздовж тієї ж осі, взятій з протилежним знаком.