10.2. Закон повного струму в інтегральній формі
Кількісний
зв’язок між циркуляцією вектора
по замкненому контуру і струмом усередині
цього контуру визначається законом
повного струму в інтегральній формі:
інтеграл
від напруженості магнітного поля уздовж
будь-якого замкненого контуру рівний
повному струмові, який пронизує цей
контур (рис.10.2), тобто:
.
(10.3)
Під повним струмом розуміють увесь струм (струм провідності та струм зміщення), що пронизує деякий контур інтегрування.
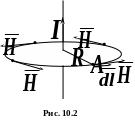
Інтегральну форму закону повного струму (10.3) застосовують тоді, коли може бути використана симетрія в магнітному полі. Так, наприклад, напруженість поля в деякій точці А, що знаходиться в полі одинокого прямого проводу зі струмом (рис. 10.2) згідно з законом повного струму визначимо наступним чином.
Проведемо
через точку А
коло радіусом
так, щоб центр кола знаходився на осі
проводу. Завдяки симетрії напруженість
поля в усіх точках кола чисельно одна
й та ж (
)
і напрямок напруженості співпадає з
дотичною до кола (
).
Тоді у відповідності з (10.3):
.
Звідси напруженість магнітного поля:
.
(10.4)
Таким чином, при зростанні відстані від осі проводу напруженість магнітного поля зменшується за гіперболічним законом.
Якщо
якесь поле має складний характер і не
вдається скласти замкнений контур, всі
точки якого знаходилися б у симетричних
умовах, то використати інтегральну
форму запису закону повного струму для
знаходження напруженості в будь-якій
точці поля неможливо, так як
не можна буде винести з-під знаку
інтеграла (
).
10.3. Закон повного струму в диференціальній формі. Ротор напруженості
Співвідношення (10.3) справедливе для контурів будь-яких розмірів, в тому числі й для досить малих.
Виділимо
в деякому середовищі (рис. 10.3) невеликий
контур і складемо вздовж нього циркуляцію
вектора
,
яка рівна струмові, що пронизує площадку
,
обмежену цим контуром.
Якщо
площадка досить мала, то можна вважати,
що густина струму
в межах цієї площадки одна й та ж (
)
і струм, який пронизує площадку
:
,
де
– проекція вектора густини струму
на нормаль
до площадки
,
тобто на напрямок вектора
.
Тоді формула (10.3) відносно площадки запишеться:
.
(10.5)
З
а
додатний напрямок нормалі до площадки
приймають напрямок руху вістряка
правоходового гвинта, головка якого
обертається в напрямку обходу контуру
при складанні циркуляції вектора
.
Поділимо обидві частини рівності (10.5) на і спрямуємо до нуля, що відповідає стягуванню розглядуваної площадки до нуля.
Границя цього співвідношення:
.
(10.6)
Ліва
частина рівності (10.6) являє собою проекцію
ротора
на напрямок нормалі
до площадки
.
Тоді вираз (10.6) прийме вигляд:
.
(10.6,а)
Якщо площадку зорієнтувати в просторі так, щоб напрямок нормалі до неї співпадав з напрямком вектора густини струму в даній точці поля, то замість рівності проекцій двох векторів (10.6, а), можна записати рівність самих векторів:
.
(10.7)
Формула (10.7) виражає закон повного струму в диференціальній формі.
Ротор може бути визначений як функція, яка характеризує поле в даній точці у відношенні до здатності утворення виходів.
Рівняння (10.7) записане в загальній формі, безвідносно до будь-якої координатної системи, і в кожній системі координат воно розкривається по-своєму.