3. Определение потерь электрической энергии в рельсовом токопроводящем стыке
Определение потерь электрической энергии в стыках:
где
- ток в рельсах, А;
- число часов году;
- сопротивление
соединителя, Ом;
-
переходное сопротивление «рельс –
накладка» при незачищенных и
зачищенных поверхностях контактирования
накладки и рельсов.
При не зачищенной поверхности контактирования накладки и рельсов.
При зачищенной поверхности контактирования накладки и рельсов.
Результаты расчета занесены в таблицу 3.
Таблица 3
Зависимость потерь электрической энергии от усилия натяжения стыковых болтов
Усилие натяжения стыковых болтов, кН |
Потери электрической энергии в стыках, кВт.ч |
|
Не зачищенная поверхность контактирования |
Зачищенная поверхность контактирования |
|
10 |
44,76 |
7,13 |
20 |
39,96 |
5,53 |
30 |
37,06 |
4,76 |
40 |
35 |
4,27 |
50 |
33,4 |
3,93 |
60 |
32.1 |
3,66 |
70 |
31 |
3,46 |
По полученным данным строим график зависимости потерь электрической энергии в рельсовом токопроводящем стыке при незачищенных и зачищенных поверхностей контактирования накладки и рельсов от усилия натяжения стыковых болтов, рисунок 3.
Рис. 3. График зависимости потерь электрической энергии в рельсовом токопроводящем стыке от усилия натяжения стыковых болтов
Вывод: Из рисунка 3 видно, что наименьшие потери электрической энергии в рельсовом токопроводящем стыке возникают при зачищенной поверхности контактирования накладки и рельсов и практически не изменяются от усилия натяжения стыковых болтов.
4. Расчет тарельчатых пружин для рельсовых стыков
Тарельчатая пружина
(рис. 4) представляет собой малоподъемную
коническую оболочку, которая в процессе
деформации получает значительные
перемещения. При расчете тарельчатых
пружин определяют величину сжимающей
силы
при заданной
осадке
и геометрических размерах
и
Затем
определяют напряжения в кромках пружины
и
Рисунок 4. Тарельчатая пружина.
3.1. Зависимость между и перемещением пружины в любой точке характеристики:
(5)
где
;
(6)
=1,72
– отношение наружного диаметра
тарельчатой пружины к внутреннему
диаметру;
=55000 Н – усилие, воспринимаемое пружиной;
E =2100 Н/мм2 – модуль нормальной упругости;
S – толщина пружины, мм;
f =0 2,5 мм – осевое перемещение пружин, мм;
h – высота нагружаемой пружины, мм;
=0,3
– коэффициент Пуассона [1с. 8];
D – наружный диаметр тарельчатой пружины, см.
При осевом перемещении пружин f=0:
При осевом перемещении пружин f=0,5:
При осевом перемещении пружин f=1:
При осевом перемещении пружин f=1,5:
При осевом перемещении пружин f=2:
При осевом перемещении пружин f=2,5:
По полученным данным строим график зависимости усилия воспринимаемой пружины и перемещением пружины f, рисунок 5.
Рисунок 5. График зависимости усилия воспринимаемой пружины и перемещением пружины f.
Вывод: Из рисунка 5 видно, что чем больше усилие на тарельчатую пружину, тем больше она перемещается.
3.2. Толщину пружины можно определить по формуле:
;
(7)
где
=1.95
мм – наибольший изгиб;
=55000 Н – усилие, воспринимаемое пружиной;
– допустимое
напряжение.
3.3. Наружный диаметр пружины:
;
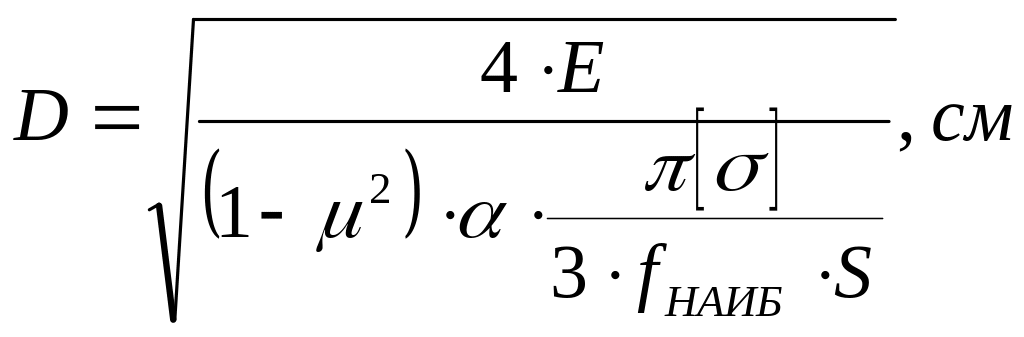(8)
где =1.95 мм – наибольший изгиб;
E =2100 Н/мм2 – модуль нормальной упругости;
S=10.6 мм – толщина пружины;
– допустимое
напряжение.
3.4. Высота нагруженной пружины:
;
(9)
где =1.95 мм – наибольший изгиб;
S=10.6 мм – толщина пружины.
3.5. Объем металла в тарельчатой пружине:
;
(10)
где S =0.106 см толщина стенки пружины;
D =16.12 см наружный диаметр тарельчатой пружины;
d =9.3 см– внутренний диаметр тарельчатой пружины.
3.6. Масса тарельчатой пружины:
;
(11)
где = 7,85 г/см3 – плотность стали [1с. 9];
S=0.106 см толщина пружины;
D=16.12 см наружный диаметр тарельчатой пружины;
d=9.3 см – внутренний диаметр тарельчатой пружины.
При нагружении в кромках тарельчатой пружины возникают напряжения растяжения и сжатия, которые определяются по следующим уравнениям.
При уменьшении осадки пружины (сплющивании) в её четырех кромках возникают напряжения, от правильного выбора которых зависит долговечность пружин. Эти напряжения определяются по следующим формулам:
3.7. I – верхняя кромка отверстия:
;
(12)
3.8. II – нижняя кромка отверстия:
;
(13)
3.9. III – нижняя кромка наружного диаметра:
;
(14)
3.10. IV – верхняя кромка наружного диаметра:
;
(15)
где S =10.6 мм – толщина стенки пружины;
D=16.12 см – наружный диаметр тарельчатой пружины;
d=9.3 мм – внутренний диаметр тарельчатой пружины;
= 0.3 – коэффициент Пуассона;
f =0 2.5 мм – осевое перемещение пружины;
E =2100 Н/мм2 – модуль нормальной упругости;
h=3.85 мм – высота нагруженной пружины;
α=0.62;
β=1.14;
γ=1.28.
I – верхняя кромка отверстия:
При осевом перемещении пружин f=0:
При осевом перемещении пружин f=0,5:
При осевом перемещении пружин f=1:
При осевом перемещении пружин f=1,5:
При осевом перемещении пружин f=2:
При осевом перемещении пружин f=2,5:
II – нижняя кромка отверстия:
При осевом перемещении пружин f=0:
При осевом перемещении пружин f=0,5:
При осевом перемещении пружин f=1:
При осевом перемещении пружин f=1,5:
При осевом перемещении пружин f=2:
При осевом перемещении пружин f=2,5:
III – нижняя кромка наружного диаметра:
При осевом перемещении пружин f=0:
При осевом перемещении пружин f=0,5:
При осевом перемещении пружин f=1:
При осевом перемещении пружин f=1,5:
При осевом перемещении пружин f=2:
При осевом перемещении пружин f=2,5:
IV – верхняя кромка наружного диаметра:
При осевом перемещении пружин f=0:
При осевом перемещении пружин f=0,5:
При осевом перемещении пружин f=1:
При осевом перемещении пружин f=1,5:
При осевом перемещении пружин f=2:
При осевом перемещении пружин f=2,5:
По полученным
данным строим график зависимости
напряжения растяжения и сжатия
,
от перемещением пружины
f,
рисунок 6.
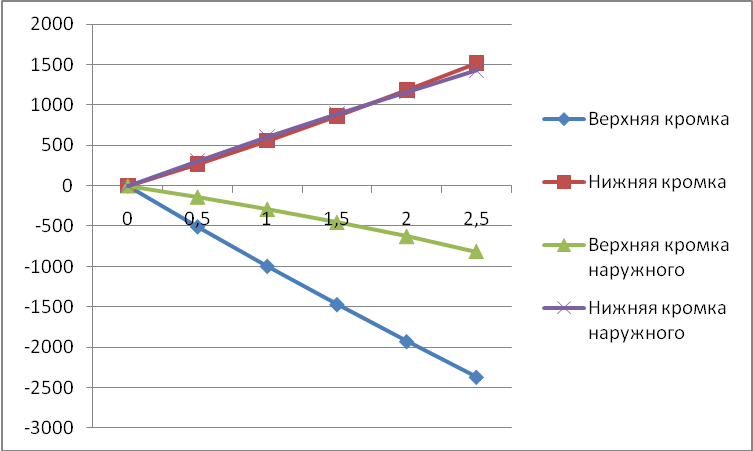
Рисунок 6. График зависимости напряжения растяжения и сжатия , от перемещением пружины f.
Вывод: Из рисунка 6 видно, что кромки пружины работают по парно. Верхняя кромка отверстия – I, и верхняя кромка наружного диаметра – IV тарельчатой пружины работают на сжатие, а нижняя кромка отверстия – II, и нижняя кромка наружного диаметра – III работают на растяжение.