Аналитичность преобразования Фурье.

Гладкость функции зависит от скорости стремления к нулю при . Пусть интегрируемым является произведение  – фиксированная постоянная.

По определению для . Определим этим же равенством функцию комплексного аргумента :

Этот интеграл сходится в полосе , так как и для всех действительных .

Утверждение. – аналитическая функция комплексного переменного в полосе . При эта функция стремится к нулю равномерно по .

Доказательство. В каждой внутренней точке полосы эта функция комплексного аргумента дифференцируема: при формальном дифференцировании по имеем

этот интеграл равномерно сходится в некоторой окрестности точки (не выходящей за пределы полосы) и представляет, следовательно, производную функции . Функция ограничена во всей указанной полосе:

Отсюда следует, в частности, что последовательности функций , сходящейся по отвечает последовательность , равномерно сходящаяся во всей полосе .

Далее, можно утверждать, что функция стремится при к нулю равномерно по , . Действительно, это имеет место для преобразования Фурье характеристической функции интервала :

,

поскольку числитель полученного выражения ограничен при ( ). К общему случаю можно перейти обычным предельным переходом от ступенчатых функций.

Утверждение доказано.

Отметим, что в силу последнего свойства в формуле обращения можно произвести интегрирование не только по вещественной оси, но по любой параллельной прямой, лежащей в указанной полосе -плоскости, так что

В приложениях иногда приходится применять преобразования Фурье к функциям, имеющим разное асимптотическое поведение при и .

Теорема. Пусть – локально абсолютно интегрируемая функция вещественного аргумента такая, что при и при , причём . Тогда интеграл

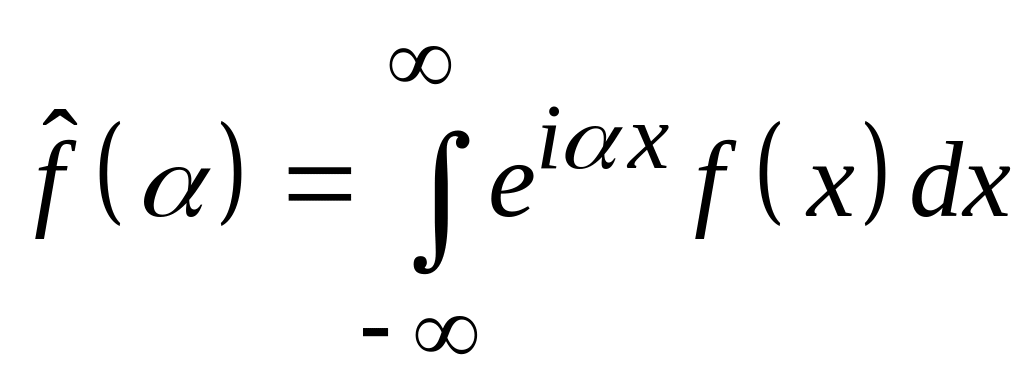
определяет аналитическую функцию от в полосе . При любом имеет место формула обращения

,

если только она имеет место хотя бы для одного .

Замечание. В приведенной ниже теореме доказано, что формула обращения имеет место для любого .

Доказательство. Сходимость интегралов от и от в полосе следует из локальной интегрируемости и оценок при и :

при , так как ,

при так как .

Стремление к нулю при сохраняется при умножении экспонент на .

Убедимся в справедливости формулы обращения, для чего подставим в неё

Возможность обращения преобразования Фурье на функции при любом вытекает из предположения о его обратимости при , так как 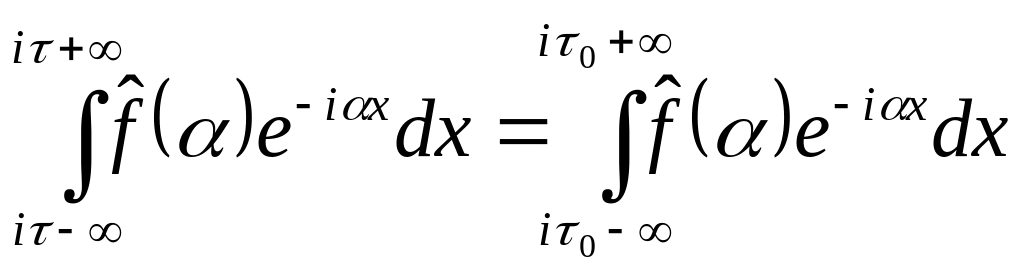в силу теоремы Коши и равномерного по стремления к нулю функции .

Теорема доказана.

Переход к комплексным значениям аргумента образа преобразования Фурье позволяет применять его к функциям вещественного аргумента, которые на всей вещественной оси могут быть неинтегрируемыми.

Пример.

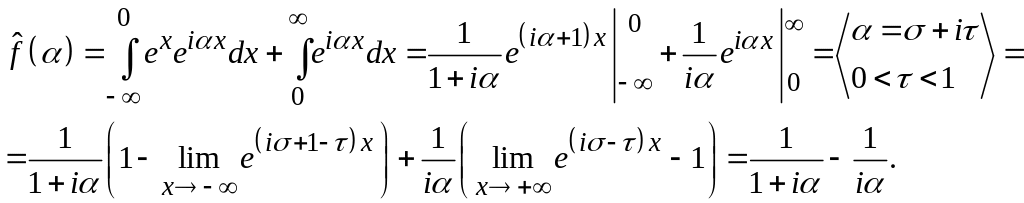
Получилась функция, аналитическая в полосе (мероморфная во всей плоскости, с полюсами на границах полосы). Отметим, что первый интеграл сходится только при , а второй – при .

Обращением предыдущей теоремы является следующая

Теорема [6]. Пусть функция , , голоморфна в полосе и пусть равномерно, когда в полосе , где – произвольное положительное число. Тогда для функции

,

где , а – вещественно, имеет место соотношение

.

Кроме того, при и при , где –произвольное, сколь угодно малое положительное число.

Функцию , определенную в утверждении теоремы можно считать решением интегрального уравнения

.

Доказательство. Проверим непосредственно последнее равенство:

.

Пусть в этом равенстве. Выберем и так, что и перейдем во внутреннем интеграле на параллельную прямую для , а для – на прямую :

.

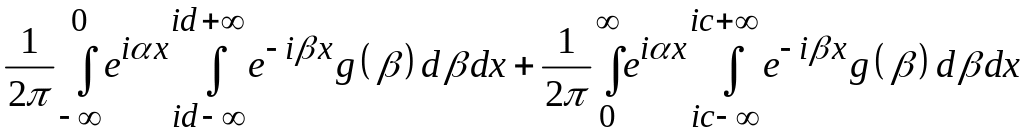Сдвиги сделаны для того, чтобы можно было поменять порядок интегрирования. До сдвигов мы имели , а после сдвигов в первом интеграле и , а во втором и . Эти неравенства гарантируют экспоненциальное убывание модуля подынтегральной функции при (с учетом при ). Отметим здесь, что абсолютная сходимость полученных повторных интегралов влечет в силу теоремы Фубини сходимость при почти всех и независимость от интеграла, определяющего функцию f(x).

После перемены порядка интегрирования и вычисления внутренних интегралов будем иметь

, где – замкнутый контур, получающийся в пределе из прямоугольника при , причем этот прямоугольник обходится в положительном направлении (против часовой стрелки). Так как по условию равномерно в полосе , то интегралы по вертикальным сторонам прямоугольника в пределе обращаются в нуль.

По теореме Коши о вычетах (интегральная формула Коши) имеем .

Далее, если при и при , то из формулы следует, что голоморфна в полосе . Однако, по условию голоморфна при . Следовательно, можно положить , , где – произвольно малое положительное число.

Теорема доказана.