Задание 8: 8.1-8.6

Тема 6: корреляционно-регрессионный анализ

Корреляционно-регрессионный анализ включает в себя измерение тесноты, направления связи и установление аналитического выражения (формы) связи.

Если результативный признак с увеличением факторного признака равномерно возрастает или убывает, то такая зависимость называется линейной и выражается уравнением прямой:

,

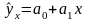где у – индивидуальные значения результативного признака;

х – индивидуальные значения факторного признака;

а₀, а₁ – параметры уравнения прямой (уравнения регрессии);

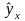– теоретическое значение результативного признака.

Параметры уравнения прямой а₀ и а₁ определяются путем решения системы нормальных уравнений, полученных методом наименьших квадратов:

Средний коэффициент эластичности определяется для уравнения прямой по формуле:

.

Линейный коэффициент корреляции применяется для измерения тесноты связи только при линейной форме связи и вычисляется по формулам:

.

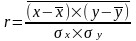Здесь черта обозначает средние величины. Используя свойства средней, получаем другую формулу:

.

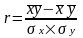Преобразуем данную формулу и получим следующую:

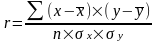или .

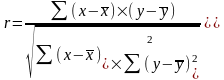Вычисление по этой формуле достаточно трудоемко, поэтому линейный коэффициент корреляции можно вычислять по формуле:

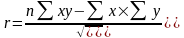
Коэффициент детерминации определяется как квадрат коэффициента корреляции:

.

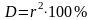Задача. Пусть по 10 однотипным предприятиям имеются следующие данные о выпуске продукции (х) в тыс. ед. и о расходе условного топлива (у) в тоннах (графы 1 и 2 таблицы).

Требуется найти уравнение зависимости расхода топлива и выпуска продукции (или уравнение регрессии у по х) и измерить тесноту зависимости между ними

Решение.

А. Рассматривая уравнение регрессии в форме линейной функции вида , параметры данного уравнения (а₀ и а₁) найдем из системы нормальных уравнений

,

а необходимые для решения суммы 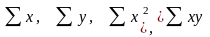рассчитаны в таблице:

Вспомогательная таблица для расчета параметров а₀ и а₁

х	у	х2	ху		у2
1	2	3	4	5	6
5	4	25	20	3,9	16
6	4	36	24	4,4	16
8	6	64	48	5,5	36
8	5	64	40	5,5	25
10	7	100	70	6,6	49
10	8	100	80	6,6	64
14	8	196	112	8,8	64
20	10	400	200	12,1	100
20	12	400	240	12,1	144
24	16	576	384	14,3	256
125	80	1961	1218	80	770

Подставляем их в уравнение и решаем систему:

.

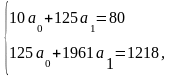
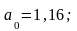
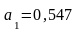Искомое уравнение прямой:

.

Параметр уравнения регрессии а₁ = 0,547 показывает, что с увеличением объема продукции на 1 тыс. руб. расход топлива возрастает на 0.547 т.

Б. Для измерения тесноты зависимости между у и х воспользуемся прежде всего линейным коэффициентом корреляции (поскольку зависимость рассматривалась линейной):

а) по формуле 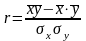находим ; ; ; .

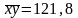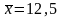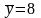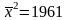Определяем σ_х и σ_у, предварительно найдя и

.

.

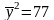
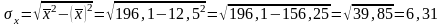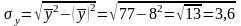Значение линейного коэффициента корреляции r = 0,96 (т.е. близкое к единице) характеризует не только меру тесноты зависимости вариации у от вариации х, но и степень близости этой зависимости к линейной;

б) воспользуемся еще одной формулой линейного коэффициента корреляции:

,

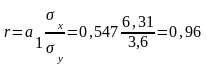т.е. результат тот же.

При расчете коэффициента корреляции, особенно если он исчислен для небольшого числа наблюдений (n), очень важно оценить его надежность (значимость). Для этого рассчитывается средняя ошибка коэффициента корреляции (σ_r) по формуле

,

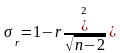где (n – 2) – число степеней свободы при линейной зависимости.

А затем находится отношение коэффициента корреляции к его средней ошибке, т.е. , которое сравнивается с табличным значением t-критерия Стъюдента.

В рассматриваемом примере средняя ошибка коэффициента корреляции

,

а

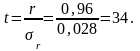
По таблице находим, что при числе степеней свободы k = 10 – 2 = 8 и уровне значимости α = 0,05 табличное (критическое, пороговое) t равно 2,306, т.е. t_табл = 2,306.

Поскольку фактическое (расчетное) t больше табличного, t_факт > t_табл, то линейный коэффициент корреляции r = 0,96 считается значимым, а связь между x и y – реальной.

Коэффициент эластичности равен: 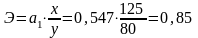. Это означает, что при изменении выпуска продукции на 1% результативный признак увеличивается на 0,85%.

Коэффициент детерминации равен: 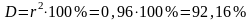. Это означает, что 92,16% изменения результативного признака объясняется изменением факторного признака.