Вариант 1

1. Решите систему уравнений с помощью формул Крамера

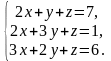
2. Даны векторы , , .

а) Вычислите произведение векторов 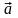, и ;

б) Найдите модуль векторного произведения и ;

в) Проверьте, будут ли коллинеарны или ортогональны и ;

г) Проверьте, будут ли компланарны векторы , и .

3. Составьте уравнение прямой , проходящей через т. А (-2;3) и начало координат.

4. Найдите следующие пределы: а) ; б) .

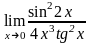5. Вычислите производные следующих функций:

а) ; б) .

6. Найдите интегралы: а) ; б) .

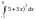7. Решите дифференциальное уравнение первого порядка с разделяющимися переменными .

8. Исследуйте ряд на сходимость .

9. В урне 2 синих, 2 красных и один желтый шар. Определите вероятность того, что взятый наугад шар будет синего цвета.

Вариант 2

1. Решите систему уравнений с помощью формул Крамера

2. Даны векторы , , .

а) Вычислите произведение векторов , и ;

б) Найдите модуль векторного произведения и ;

в) Проверьте, будут ли коллинеарны или ортогональны и ;

г) Проверьте, будут ли компланарны векторы , и .

3. Составьте уравнение прямой , проходящей через т. В (4;8) и начало координат.

4. Найдите следующие пределы: а) ; б) .

5. Вычислите производные следующих функций: а) ; б) .

6. Найдите интегралы: а) ; б) .

7. Решите дифференциальное уравнение первого порядка с разделяющимися переменными .

8. Исследуйте ряд на сходимость .

9. Из корзины, в которой 5 красных, 7 белых и 3 желтые розы, наугад достают один цветок. Определите вероятность того, что достали цветок желтого цвета.

Вариант 3

1. Решите систему уравнений с помощью формул Крамера

2. Даны векторы , , .

а) Вычислите произведение векторов , и ;

б) Найдите модуль векторного произведения и ;

в) Проверьте, будут ли коллинеарны или ортогональны и ;

г) Проверьте, будут ли компланарны векторы , и .

3. Составьте уравнение прямой проходящей через точки А (3;5) и

В (-1;-10).

4. Найдите следующие пределы: а) ; б) .

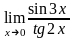5. Вычислите производные следующих функций:

а) ; б) .

6. Найдите интегралы: а) ; б) .

7. Решите дифференциальное уравнение первого порядка с разделяющимися переменными .

8. Исследуйте ряд на сходимость .

9. Из колоды игральных карт (36 карт) достают одну. Определите вероятность, что достали даму.

Вариант 4

1. Решите систему уравнений с помощью формул Крамера

2. Даны векторы , , .

а) Вычислите произведение векторов , и ;

б) Найдите модуль векторного произведения и ;

в) Проверьте, будут ли коллинеарны или ортогональны и ;

г) Проверьте, будут ли компланарны векторы , и .

3. Составьте уравнение прямой проходящей через точки А (-3;1) и

В (4;-2).

4. Найдите следующие пределы: а) ; б) .

5. Вычислите производные следующих функций: а) ; б) .

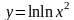6. Найдите интегралы: а) ; б) .

7. Решите дифференциальное уравнение первого порядка с разделяющимися переменными .

8. Исследуйте ряд на сходимость .

9. В классе 10 девочек и 15 мальчиков. Какова вероятность, что вызванный к доске ученик будет мальчиком?