Определить

1) плотность потока собственного излучения;

2) плотность потока эффективного излучения;

3) длину волны в соответствии с законом смещения Вина;

4) привести качественный график спектральной плотности лучеиспускательной способности с учетом пункта .

Ответ: Е₀ = 523.6 кВт/ м² ; Е_ЭФФ = 543.6 кВт/м² ; λ_М = 1.26 мкм (3 б)

Для определения собственного излучения необходимо знать степень черноты ε тела, которая для серых тел равна поглощательной способности А. Сумма поглощательной и отражательной способностей равна 1

А + R = 1 Отсюда

Плотность потока собственного излучения (интегральная лучеиспускательная способность) определим по закону Стефана-Больцмана с учетом степени черноты тела

Длину волны λ_m определим по закону смещения Вина

Сумма собственного и отраженного от тела излучения называется эффективным излучением

6.19. Горизонтальная труба с внешним диаметром d = 50 мм и длиной l = 2 м охлаждается при свободной конвекции воздуха, температура которого t_ж = 20 ⁰С. Определить коэффициент теплоотдачи и количество отведенного тепла, если температура стенки трубы t_ст = 200 ⁰С .(свойства воздуха брать при его температуре; определяющий размер – диаметр трубы; лучистый теплообмен не учитывать (Ответ.;) (3 б)

Соответствующие температуре воздуха t _Ж = 20 ⁰С параметры находим из таблицы.

ν = 15.61•10^-6 м² / с; β = 3.42 10^-3 К^-1 ; λ = 2.58 10^-2 Вт/ м К; Рr = 0.71

Из таблицы находим коэффициенты С и n:

С = 0.5, n = 0.25

Определяем число Нуссельта

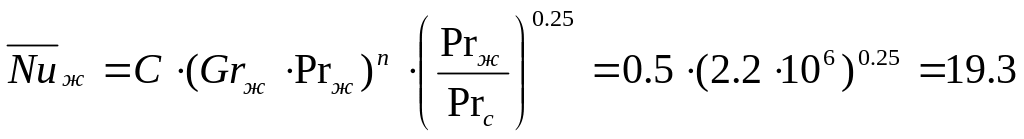
Откуда

Тепловой поток (потери тепла)

6.20 Приведите Р-Т фазовую диаграмму для воды и с ее помощью объясните возможность

катания на коньках (на льду) без поперечного скольжения. (1 б)

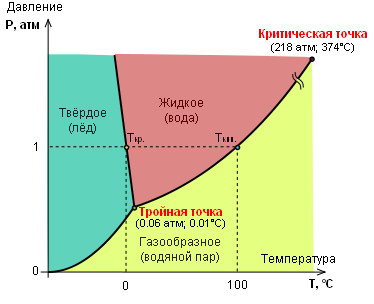
Вариант 7

7.1 Приведите качественные графики изменения теплового потока и температур в двухслойной плоской стенке, коэффициенты теплопроводности которых изменяются с температурой как: ; ; _{Коэффициенты в уравнениях постоянны Направление теплового потока показано стрелкой (2 б)}

2 1

T2 Q

Т₁

T3

7.2. Между двумя адиабатами 1 и 2 осуществляются два изотермических процесса (см.рисунок) при температурах Т₁ и Т₂ = 0.5•Т₁

1) Как соотносятся изменения энтропий и в этих процессах ? (2 б) 2) Обоснование ответа (аналитическое и/или графическое)

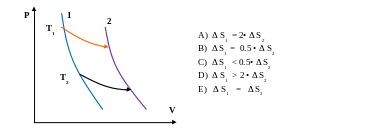
В адиабатных процессах изменение энтропии равно нулю

7.3. Некоторое количество аргона расширяется: сначала адиабатно, а затем – изобарно. Конечная температура газа равна начальной. При адиабатном расширении газ совершает работу, равную А₁ = 10 кДж. Чему равна работа газа за весь процесс.

Работа единицы количества идеального газа в адиабатном процессе 1-2 равна убыли внутренней энергии газа (берем по модулю)

Работа в изобарном процессе 2-3 равна разности подведенного тепла в этом процессе и изменении внутренней энергии

(Последний вывод можно было написать и из определения газовой постоянной : она равна работе единицы количества вещества в изобарном процессе при ΔТ = 1 К )

Подставим в эту формулу значение ΔТ из первой формулы

→

Теперь найдем полную работу за два процесса

(3 б)

7.4. Чему равно изменение энтропии при изохорном нагревании водорода массой , если давление газа увеличилось в два раза.?

=m* dlya 1 kg, process izohorniy, poetomu P1/P2=T1/T2=2

(2 б)

A) 143.4 Дж/К

B) 35.85 Дж/К

C) 17.9 Дж/К

D) 140.5 Дж/К

E) 281. 22 Дж/К

7.5. Тепловая машина совершает обратимый цикл, представленный ниже на T-S диаграмме. Получите формулу для определения КПД этого цикла через максимальную Т₁ и минимальную Т₂ температуры газа (1 б)

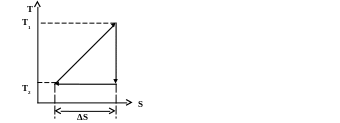
На выбор одно из двух:

1)

2)

7.6 На рисунке в T-S координатах приведен процесс 1-2-3-4-5-6.

1) Какой геометрической величине численно равна теплота в этом процессе

(в терминах площади) ? 4-5-6 (1 б)

2) Теплота процесса

А) ; В) ; С) нельзя сказать определенно

Т 2

3

1

6 5

4

7 8 S

7.7. В координатах приведите изотерму (1) изобару (2), изохору (3) и адиабату (4) и покажите области, где (2 б)

1) теплота отводится от газа – левее от изотермы

2) внутренняя энергия газа уменьшается – зона выше изотермы

3) теплоемкость отрицательна - С

(для удобства можно привести несколько графиков со всеми указанными процессами)

7.8 Определить количество тепла, необходимого для перевода трех молей одноатомного идеального газа из состояния 1 в состояние 3. В состоянии 1 температура газа Т₁= 300 К (Ответ: кДж) (3 б)

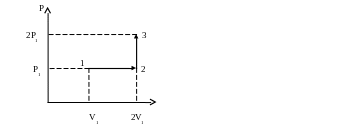
2V1/V1=T2/T1 → T2=2T1 →2P1/P1=T3/T2 →T3=2T2

n= koli4estvo moley

P1*(dV) + 3/2*n*R*(T2-T1) + 3/2*n*R*(T3-T2) = nRT1 + 3/2*n*R*(T3-T1)

n= P1V1/RT1→ P1V1=nRT1

7.9. 1) Приведите фазовую диаграмму воды.

2) Укажите характерные точки на этой диаграмме

3) Приведите значения параметров состояния в этих точках

4) Какое условие необходимо выполнить, чтобы перевести вещество из газового

состояния в жидкое ? (2 б)

1),2),3)

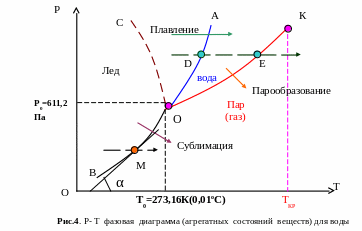
ОК – кривая испарения (жидкость - пар)

ОА – кривая плавления (лед - вода)

ОВ – кривая возгонки (лед - пар)

т.О – тройная точка

К – критическая точка

4) Для того, чтобы перевести вещество из газового состояния в жидкое необходимо при давлении много больше 611,2 Па понизить температуру не ниже 273,16 К (0,01⁰С), т.е. уменьшая температуру увеличивать температуру.

7.10. Давление углекислого газа (к = 1.33) на входе в сужающееся сопло Р₁ = 30 бар, давление окружающей среды Р_окр = 10 бар. Чему равно давление Р₂ на срезе сопла ?

А) 33.3 бар, В) 30. 7 бар, С) 29.3 бар, D) 14.64 бар, E) 21.6 бар

Решение. Отношение давлений β = 10/30 = 0.333. это меньше критического для СО₂, равного 0.54; режим истечения будет критический.

Давление определяется по формуле Р = β •Р₁ = 0.54 · 30 = 16,2 бар