Решение:

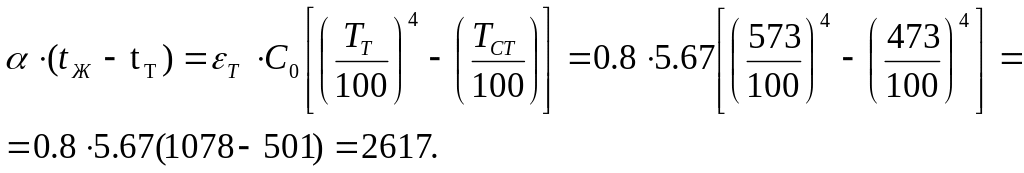
3.19. Тонкая пластина длиной l = 5 м и шириной а = 3 м обтекается продольным потоком воздуха (см. рис.) Скорость и температура потока равны ω₀ = 2 м/с; t_Ж =10 ⁰C. Температура поверхности пластины t_C = 80 ⁰C. Определить средний по длине коэффициент теплоотдачи и количество тепла , отдаваемое пластиной воздуху.

(Формулу взять из таблицы в зависимости от режима течения; при обтекании пластины; принять ; свойства воздуха брать при его температуре; лучистый теплообмен не учитывать). (Ответ ; ) (3 б)

1)Напишем параметры воздуха для t_Ж =10 ⁰С (из таблицы)

ν_ж = 14.66 10^-6 м²/с; λ_ж = 2,51*10^-2 Вт/м К; Pr_ж = 0,71

2) Определим число Рейнольдса

Re_КР = 5∙10⁵ турбулентное течение

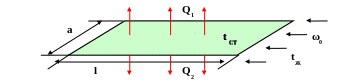
3) Средняя по длине теплоотдача в таком случае может быть рассчитана по формуле

где 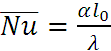; определяющим размером здесь является длина пластины.

4) Коэффициент теплоотдачи от пластины к воздуху равен

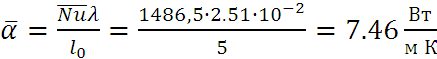
Количество передаваемого тепла с обеих сторон пластины

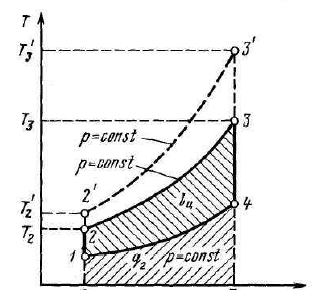
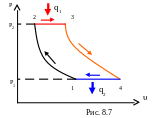
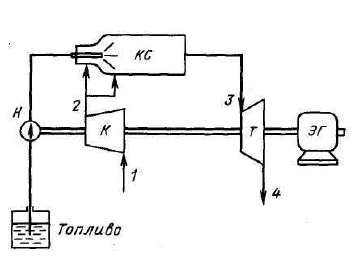
3.20. Блок схема и принцип работы ГТУ (газотурбинной установки). Цикл ГТУ при Р = const в Р-V и T-S координатах. КПД цикла (привести формулу и пояснить ее) (2 б)

`

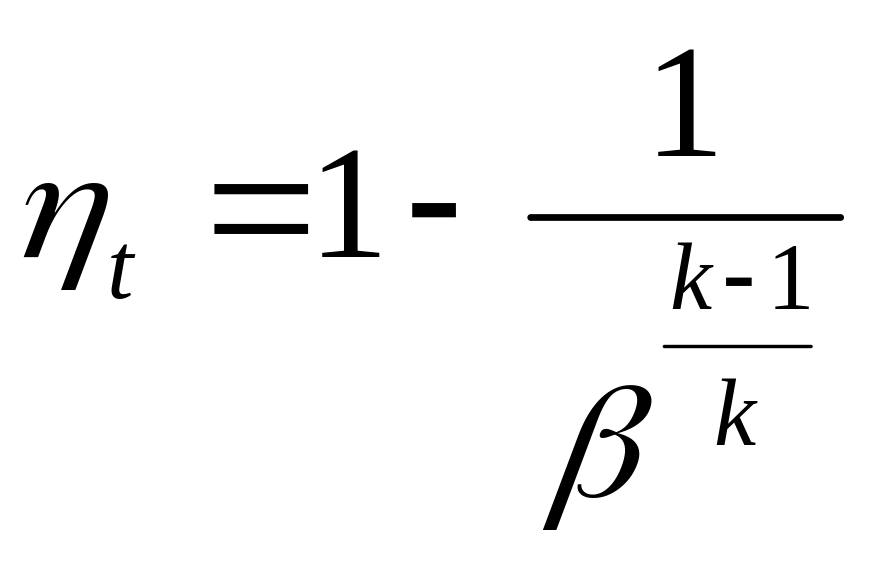
Экзаменационный билет №4

1. На рисунке в Р-V диаграмме приведены несколько процессов с идеальным газом, которые начинаются в точке О. В каких процессах теплота подводится к газу?

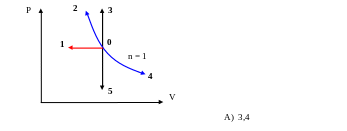
Изотермалы процесте

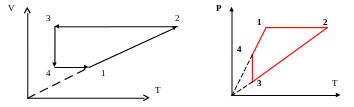
4.2. На рисунке приведен цикл идеального газа в V-Т координатах. Постройте этот цикл в P-T- координатах. Масштаб- произвольный, но сохранить закономерности. (1 б)

4.3 На рисунке в T-S координатах приведен процесс 1-2-3-4-5-6. (2 б)

1. Какой геометрической величине численно равна теплота в этом процессе

(в терминах площади) ?

2. Теплота процесса: Ответ:С

А) ; В) ; С) ; D) нельзя сказать определенно

Т 2

1 3

5 6

4

S

4.4 Воздух массой при давлении и температуре адиабатно сжимается в цилиндре до давления . Найти конечную температуру воздуха и работу, затраченную на сжатие (Ответ t₂ =229, (3 б)

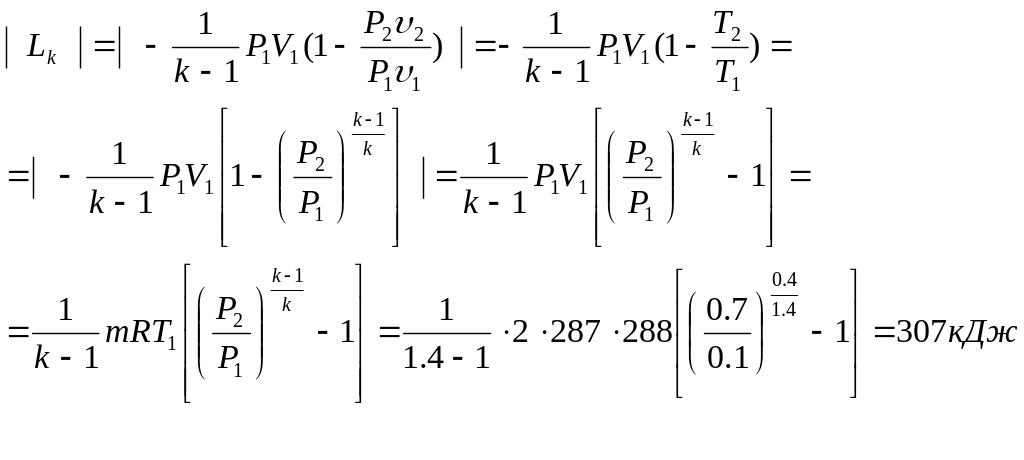
Температуру найдем из уравнения адиабаты

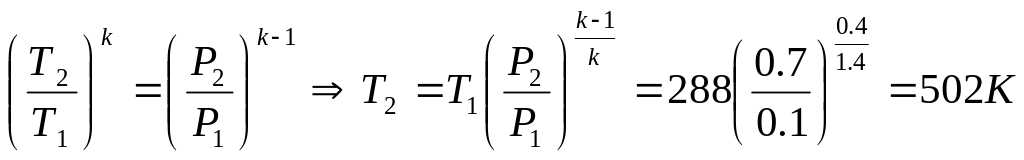
t₂ =502-273=229C

4 .5 Найти приращение энтропии воздуха при изотермическом расширении с увеличением объема в 16 раз. Теплоемкость воздуха принять постоянной (ответ ΔS=2.38 кДж/К)

4.6 Определите плотность сухого насыщенного водяного пара при температур , принимая его за идеальный газ (2 б)

;

4.7 Имеется цикл ДВС с подводом тепла при V = const: Рабочее тело – воздух (ответ: 40% ) (3 б)

1. Постройте цикл в и T--S координатах

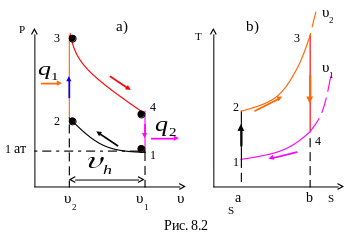
2 Определитe термический КПД цикла.

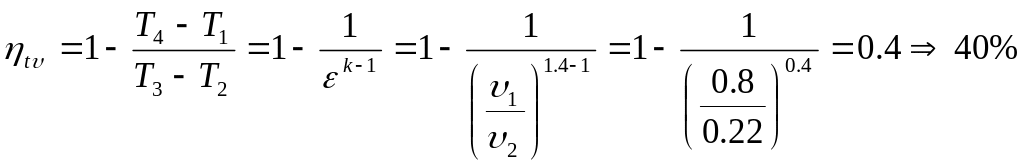
4.8. 1) Приведите пограничную кривую для фазового перехода «жидкость-пар» в

и в координатах

2) Покажите на одной из этих диаграмм величину, отражающую теплоту парообразования

3) С помощью этих диаграмм и уравнения Клапейрона-Клаузиуса покажите, как изменяется теплота парообразования с ростом температуры (2 б)

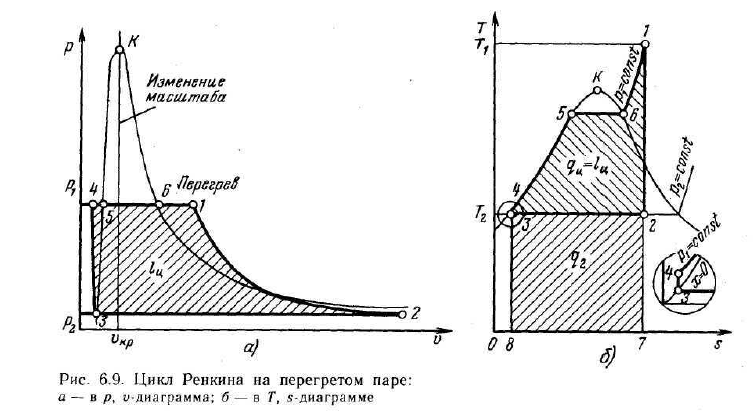
4.9. Определить среднее значение коэффициента теплоотдачи и тепловой поток при свободной конвекции от горизонтальной трубы с внешним диаметром d = 10 см и длиной l = 2 м. если температура стенки трубы t_CT = 200 ⁰С ,а температура окружающего воздуха t_Ж = 20 ⁰С (свойства воздуха брать при его температуре; определяющий размер – диаметр трубы; лучистый теплообмен не учитывать

(Ответ: ; )

Решение

Коэффициент теплоотдачи при свободной конвекции можно определить из уравнения

Постоянные С и n зависят от режима свободной конвекции и особенностей поверхности и определяются величиной комплекса

Индексы « ж» и « с» означают, что свойства жидкости берутся при температуре жидкости и температуре стенки. При вертикальной поверхности определяющим размером является высота (стенки или трубы ), а для горизонтальной трубы – наружный диаметр.

Соответствующие температуре t _Ж = 20 ⁰С параметры воздуха находим из таблицы.

ν = 15.61•10^-6 м² / с; β = 3.42 10^-3 К^-1 ; λ = 2.58 10^-2 Вт/ м К; Рr = 0.71

Найдем значение числа Гросгофа

Из таблицы 1(на лабе который) находим коэффициенты С и n для :

С = 0.5, n = 0.25

Определяем число Нуссельта

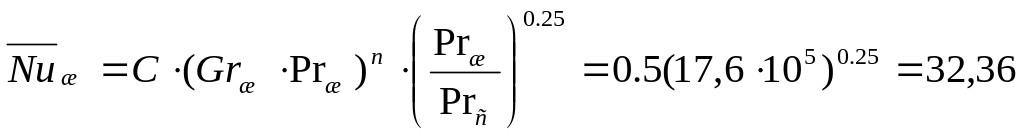
Откуда

Тепловой поток (потери тепла)

4.10. 1) Приведите качественный график спектральной плотности излучения

абсолютно черного тела с температурой поверхности Т = 6000 К ;

2) Определите длину волны в соответствии с законом смешения Вина.

3) Определите интегральную лучеиспускательную способность этого тела. (2 б)

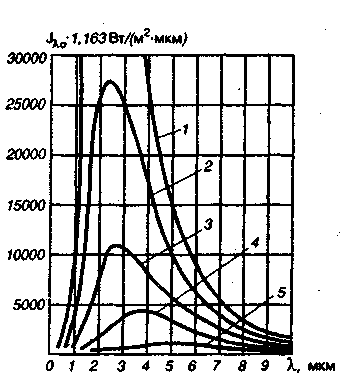
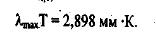
2) λ=2898/6000;

3)Закон Стефан-Вольцмана устанавливает связь между интегрального полусферического излучения абсалютно черного тела E₀ и его температурой

E₀=5.67(6000/100)⁴=7.35*10⁷ Вт/м²;

4.11 Самолет летит со скоростью ω = 3000 км/ час. Определить температуру на передней кромке крыла, считая процесс торможения потока адиабатным. Температура окружающей среды t = - 30 ⁰С, (теплоемкость воздуха принять равной значению, использованному в СРС-1) (Ответ 42 ⁰С ) (1б)

4.12 Состояние идеального газа изменяется в соответствии с уравнением , где . Определите работу, совершаемую 1 молем газа при повышении его температуры от до (3 б)

4 .13.

W, M

G,S

T,a,P

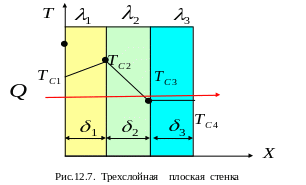
4.14. Приведите качественные графики изменения теплового потока и температур в многослойной плоской стенке, коэффициенты теплопроводности которых изменяются с температурой как: ; ; _{Коэффициенты в уравнениях постоянны. Направление теплового потока показано стрелкой (2 б)}

4.15..Имеется цилиндрическая труба радиусом с потерями тепла при граничных условиях третьего рода. Труба покрывается тепловой изоляцией переменной толщины.

Какая из кривых соответствует изменению тепловых потерь в случае, когда радиус трубы меньше критического радиуса изоляции ? (1 б)

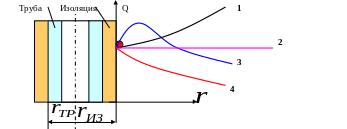С) 3 ;

4.16. Определить холодильный коэффициент цикла, если работа в цикле l = 50 кДж/кг, а отводимое тепло q₁ = 130 кДж/кг D) 1 .6;

4.17. Определить критический радиус тепловой изоляции с коэффициентом теплопроводности λ = 0.1 Вт/м К и тепловые потери с единицы длины q _l (Вт/ м) , если этой изоляцией покрыть трубу с внешним радиусом r =20 мм. Температура внутренней поверхности изоляции t_C2 = 150 ⁰C , коэффициент теплоотдачи от внешней поверхности изоляции к воздуху α₂ = 4 Вт/ м²К, температура среды t_Ж2 = 20 ⁰С. (3 б) (Ответ: r_K = 2.5 см; q = 132.7 Вт/м)

1) критический радиус равен …

2) тепловые потери с изоляцией при критическом радиусе равны ……….

3) при критическом радиусе тепловые потери : В) максимальны

Решение:

r_K= λ/ α₂ =0.1/4=0.025м=2.5 см

3.32

4.18 Получите формулу для определения доли теплоты, которая идет на изменение внутренней энергии ( ) и доли – на совершение работы ( ) в изобарном процессе. (через теплоемкости) (2 б)

Решение

отсюда или

Учитывая, что и , имеем

и далее

4.19 . Имеется двухслойная плоская стенка c параметрами δ₁ = 6 см, δ₂ = 8 см. t₁ =250 ⁰C, t₂ = 50 ⁰C. Теплопроводность материалов слоев стенок соответственно равны λ₁ = 20 Вт/м К, λ₂ = 50 Вт/ м К. ( 2 б)

1) Определить температуру t_X на границе между слоями.

2) Привести качественные графики изменения температур в слоях.

3) Определить величину теплового потока на границе между слоями

Решение:

1) ,

3)

4.20. Блок схема, принцип действия парокомпрессорной холодильной установки и ее цикл в Т –S координатах. Назначение отдельных узлов. Холодильный коэффициент. (2б)

q₂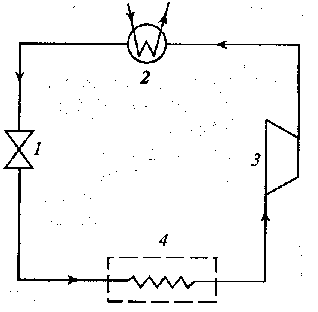

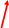q₁