Вопрос 27.

Формулы преобразования произведений в сумму (с выводом).

Используя формулы , и складывая и вычитая их почленно, получаем две формулы преобразования произведения в сумму:

и

Или

и

Используя формулы , и складывая их почленно, получаем ещё одну формулу преобразования произведения в сумму:

, или .

полученные формулы называются формулами преобразование произведения в сумму.

Вопрос 28.

Формулы преобразования сумм в произведение (с выводом).

Используя формулу получаем , обозначив и , получаем и . Подставив эти значения в равенство получаем .

Аналогично, используя формулу , получаем .

Аналогично, используя формулу , получаем и .

Полученные формулы называются формулами преобразования суммы в произведение.

Вопрос 29.

Функции их свойства.

Определение синуса, свойства и график функции .

С инусом угла называется ордината y точки P конца радиусвектора единичной окружности, образующего угол с осью абсцисс.

Функция синус

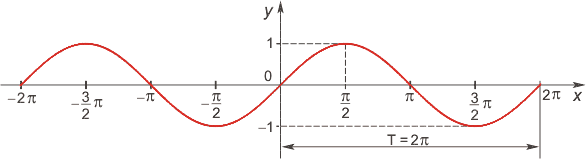
Область определения функции — множество R всех действительных чисел.

Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная.

Функция нечетная: sin(−x)=−sinx для всех х R. График функции симметричен относительно начала координат.

Функция периодическая с наименьшим положительным периодом 2π: sin(x+2πk) = sinx, где k Z для всех хR.

sinx = 0 при x = πk, kZ.

sinx > 0 (положительная) для всех x (2πk, π+2π·k), k Z.

sinx < 0 (отрицательная) для всех x (π+2π·k, 2π+2π·k), kZ.

Функция возрастает от −1 до 1 на промежутках:
Функция убывает от −1 до 1 на промежутках:
Наибольшее значение функции sin x = 1 в точках:
Наименьшее значение функции sin x = −1 в точках:

Определение косинуса, свойства и график функции .

К осинусом угла называется абсцисса x точки P конца радиусвектора единичной окружности, образующего угол с осью абсцисс.

Функция косинус

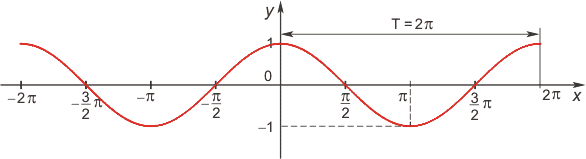
Область определения функции — множество R всех действительных чисел.

Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная.

Функция четная: cos(−x)=cosx для всех хR. График функции симметричен относительно оси OY.

Функция периодическая с наименьшим положительным периодом 2π: cos(x+2πk) = cosx, где kZ для всех хR.

cosx = 0 при
cosx > 0 для всех
cosx < 0 для всех
Функция возрастает от −1 до 1 на промежутках:
Функция убывает от −1 до 1 на промежутках:
Наибольшее значение функции cosx = 1 в точках:
Наименьшее значение функции cosx = −1 в точках:

Определение тангенса, свойства и график функции .

Т ангенсом угла называется отношение ординаты y к абсциссе x точки P конца радиусвектора единичной окружности, образующего угол с осью абсцисс.