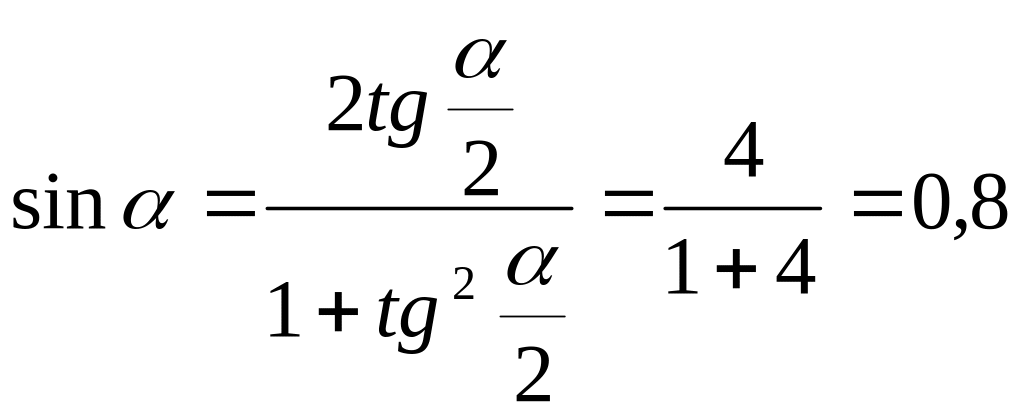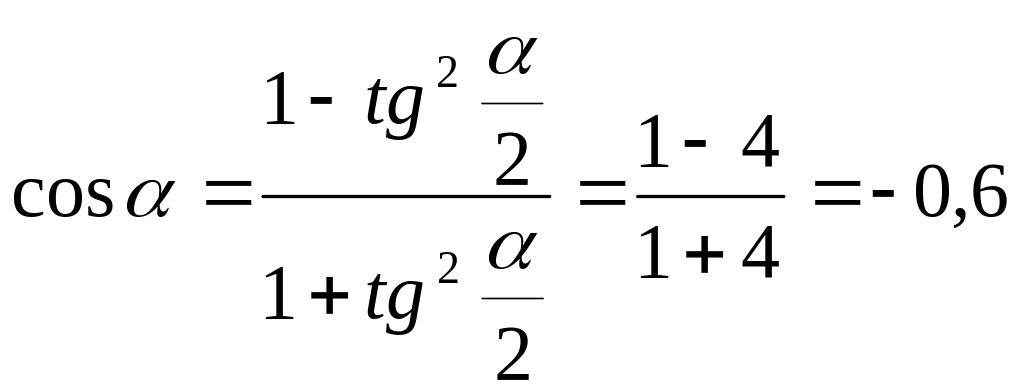- •Зачет по математике (10 класс 1 полугодие 2013/2014 учебный год).
- •Вопрос 1. Высказывание. Отрицание, конъюнкция, дизъюнкция, разность, импликация, эквиваленция высказываний, таблицы высказываний.
- •Вопрос 2. Формулы алгебры высказываний: коммутативность, ассоциативность конъюнкции и дизъюнкции (доказательство одной из них); законы поглощения для высказываний (доказательство одной из них).
- •Вопрос 4. Множество, элементы множества, пустое и универсальное множество, конечное и бесконечное множества, способы задания множества.
- •Вопрос 5. Дополнение, пересечение, объединение, разность, симметрическая разность множеств. Диаграммы Эйлера-Венна.
- •Вопрос 6.
- •Вопрос 8. Упорядоченная пара, равенство упорядоченных пар. Декартово произведение множеств а и в, декартов квадрат множества а.
- •Вопрос 9. Соответствия, область определения и область значений соответствий, способы задания соответствий, граф и график соответствий, полный образ и полный прообраз.
- •Вопрос 10.
- •Вопрос 11. Определение возрастающей и убывающей функций. Теорема о монотонной функции (с доказательством), следствия из нее.
- •Вопрос 12. Монотонные функции, свойства монотонных функции. Теорема о сумме монотонных функций (с доказательством), следствия из нее.
- •Вопрос 13. Сложная функция. Теорема о монотонности сложной функции (с доказательством).
- •Вопрос 14. Четные и нечетные функции, свойства (доказательство одного из них).
- •Вопрос 15. Ограниченность функций, наибольшее и наименьшее значение функций, экстремумы функций.
- •Вопрос 16.
- •Вопрос 17. Понятие многочлена от одной переменной, степень многочлена, нулевой многочлен, равенство многочленов, действия с многочленами.
- •Вопрос 18. Делимость многочленов, свойства делимости многочленов, метод неопределенных коэффициентов.
- •Вопрос 19. Деление многочлена на двучлен. Схема Горнера (с выводом), следствия.
- •Вопрос 20. Корень многочлена. Теорема Безу (с доказательством), следствия. Делимость двучлена на двучлен .
- •Вопрос 21. Кратность корня, понятие об основной теореме алгебры и следствия из нее. Формулы Виета (с выводом).
- •Вопрос 22. Уравнение с целыми коэффициентами, теорема о целых корнях и теорема о рациональных корнях (с доказательством).
- •Теорема о рациональных корнях многочлена.
- •Вопрос 23. Определение синуса, косинуса, тангенса, котангенса угла поворота, знаки в различных четвертях, основное тригонометрическое тождество и следствия из него (с выводом).
- •Знаки тригонометрических функций по четвертям.
- •Основное тригонометрическое тождество.
- •Вопрос 24. Формулы сложения (с выводом), , , .
- •Вопрос 25. Формулы приведения, двойных углов (с выводом).
- •Вопрос 26.
- •Вопрос 27.
- •Вопрос 28.
- •Вопрос 29.
- •Определение косинуса, свойства и график функции .
- •Функция косинус
- •Определение тангенса, свойства и график функции .
- •Функция тангенс
- •Определение котангенса, свойства и график функции .
- •Функция котангенс
- •Вопрос 30. Обратные тригонометрические функции и их свойства.
Знаки тригонометрических функций по четвертям.
Т.к. абсцисса точки положительна, когда точка лежит в I и IV координатных четвертях, и отрицательна, когда точка лежит во II и III координатных четвертях, а ордината точки положительна, когда точка лежит в I и II координатных четвертях, и отрицательна, когда точка лежит в III и IV координатных четвертях, то: синус положителен в I и II координатных четвертях, и отрицателен в III и IV координатных четвертях,
косинус положителен в I и IV координатных четвертях, и отрицателен во II и III координатных четвертях,
тангенс и котангенс положительны в I и III координатных четвертях, и отрицательны во II и IV координатных четвертях
Основное тригонометрическое тождество.
Т.к.
точка P лежит на окружности уравнение
которой
![]() ,
то её координаты (
,
то её координаты (![]() ;
;![]() )
обращают уравнение в истинное равенство.
Следовательно,
)
обращают уравнение в истинное равенство.
Следовательно,
![]()
Данное тождество называется основным тригонометрическим тождеством.
Из
него выводятся следующие следствия:
![]() и
и
![]()
![]() и
и
![]() .
.
Из
определения тангенса и котангенса
следует, что:
![]()
![]() и
и
![]() (
(![]() и
и
![]() ).
).
![]()
![]() и
и
![]() ;
;
![]()
![]() и
и
![]()
Вопрос 24. Формулы сложения (с выводом), , , .
З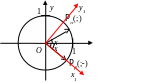 ададим
на плоскости Декартову систему координат
ададим
на плоскости Декартову систему координат
![]() и
тригонометрическую окружность. Пусть
и
и
тригонометрическую окружность. Пусть
и
![]() - произвольные положительные углы.
Проведём радиус-векторы ОР
и ОР
такие, что они образуют с положительным
направлением оси абсцисс углы
и
соответственно. В системе координат
- произвольные положительные углы.
Проведём радиус-векторы ОР
и ОР
такие, что они образуют с положительным
направлением оси абсцисс углы
и
соответственно. В системе координат
![]() точки Р
и Р
имеют координаты Р(
;
)
и Р(
точки Р
и Р
имеют координаты Р(
;
)
и Р(![]() ;
;![]() ).
).
Длина
отрезка РР
равна
![]() .
.
Или
(РР)2
=
=![]() =
=![]() =
=
=
=![]() .
.
Введём
новую систему координат
![]() ,
в которой ось Оx1
сонаправлена с радиус-вектором ОР.
В этой системе координат точка Р
имеет координаты (1;0), а Р
имеет координаты
,
в которой ось Оx1
сонаправлена с радиус-вектором ОР.
В этой системе координат точка Р
имеет координаты (1;0), а Р
имеет координаты
![]() ,
длина отрезка РР
равна
,
длина отрезка РР
равна
![]() .
Или (РР)2=
.
Или (РР)2=![]() =
=![]() .
.
Приравнивая два выражения квадрата длины отрезка РР, получаем:
![]() ,
откуда
,
откуда
![]() .
.
Подставляя
в эту формулу
вместо
и учитывая чётность функции косинус и
нечётность функции синус, получаем:
![]()
Учитывая,
что,
![]() ,
,
![]() из
полученных формулы получаем:
из
полученных формулы получаем:
![]() =
=
![]()
Т.е.![]() .
.
Подставляя
в эту формулу
вместо
и учитывая чётность функции косинус и
нечётность функции синус, получаем:
![]() .
.
![]() разделим
каждый член числителя и знаменателя на
разделим
каждый член числителя и знаменателя на
![]() и получим
и получим
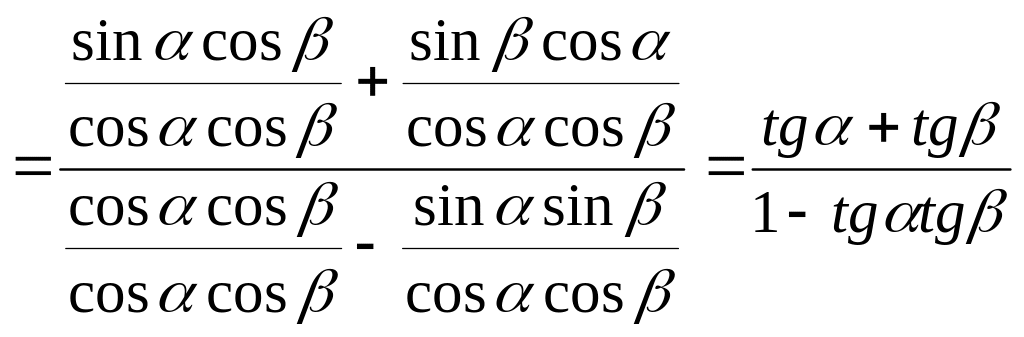 .
.
Аналогично,
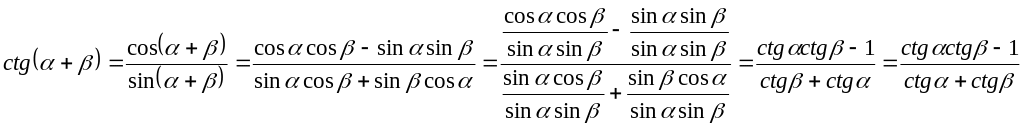 .
.
Заменив,
в полученных формулах
на
![]() ,
и учитывая нечетность функций тангенс
и котангенс, получим:
,
и учитывая нечетность функций тангенс
и котангенс, получим:
![]()
![]() .
.
Вопрос 25. Формулы приведения, двойных углов (с выводом).
Формулы приведения.
Формулы
позволяющие заменить выражение вида
![]() ,
где
,
где
![]() ,
а
,
а
![]() на
на
![]() ,
где
,
где
![]() называются формулами приведения.
называются формулами приведения.
Из
курса геометрии известно, что
,
,
![]() ,
,
![]() .
.
Т.к.
тангенс и котангенс имеют период
,
то![]() и
и
![]()
Используя
формулы
![]() ,
,
![]() ,
и
,
и
![]() ,
получаем:
,
получаем:
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
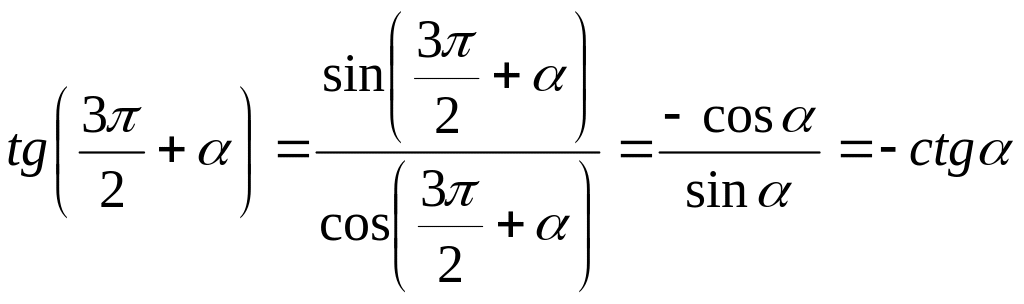
 .
.
Формулы двойного угла.
Подставляя
вместо
в формулы
,
,
![]() ,
,
![]() ,
и
получаем формулы двойного угла:
,
и
получаем формулы двойного угла:
![]()
![]()
Учитывая,
что
и
,
получаем ещё два выражения для косинуса
двойного угла:
![]() и
и
![]() .
.
![]()
![]()
Вопрос 26.
Формулы понижения степени, половинных углов, универсальная подстановка (с выводом).
Используя
формулы для
косинуса двойного угла:
![]() и
и
![]() ,
делая замену
,
делая замену
![]() получим формулы понижения степени:
получим формулы понижения степени:
![]()
![]()
![]()
![]()
![]()
![]()
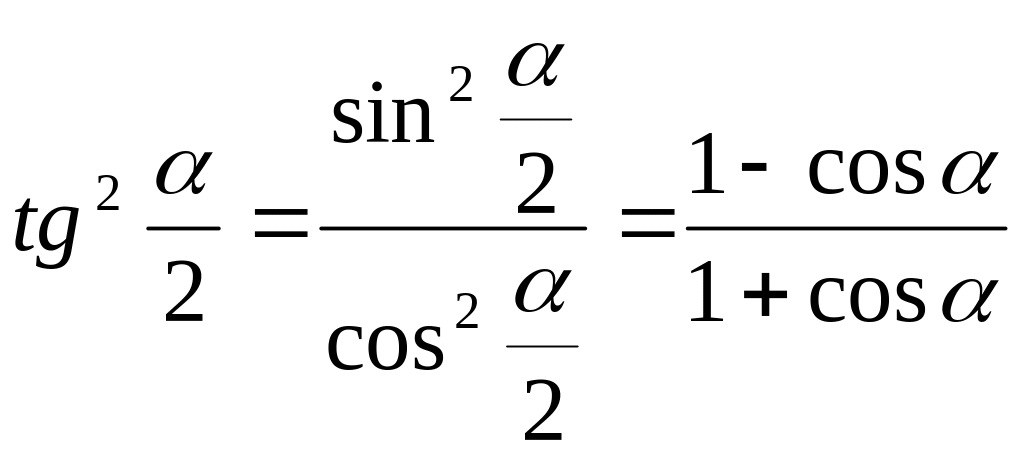
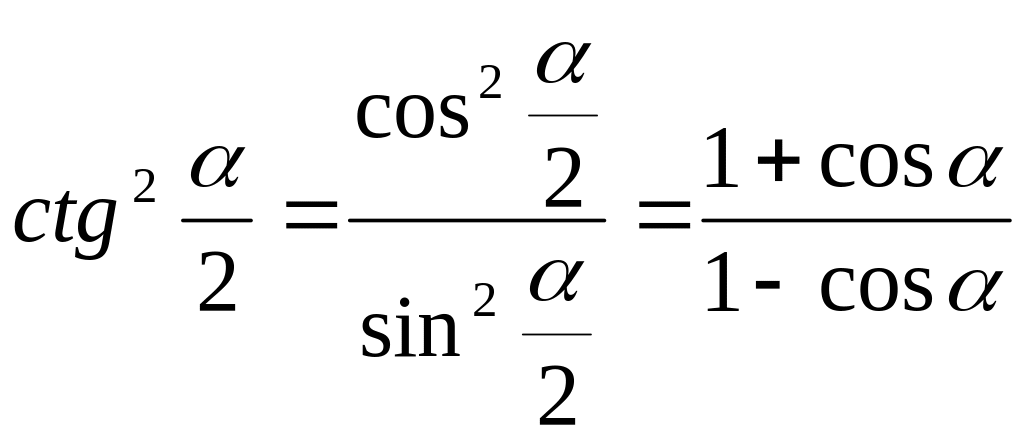
Универсальной подстановкой называется выражение тригонометрической функции через тангенс половинного угла.
 ;
; 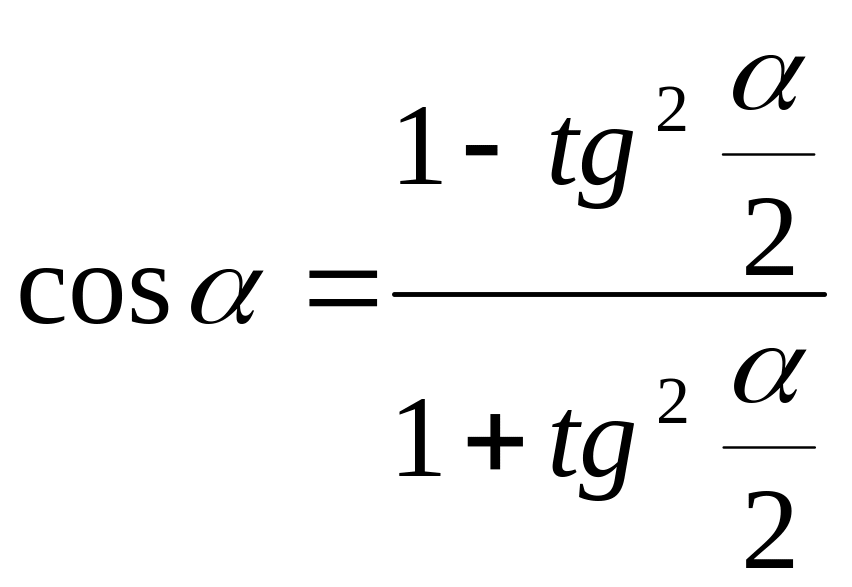 ;
;  ;
; 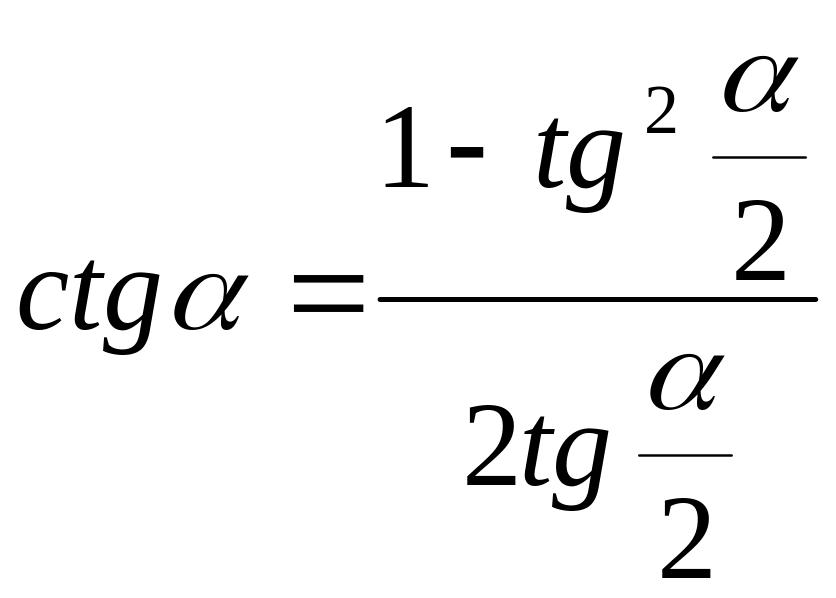 .
.
Докажем их.
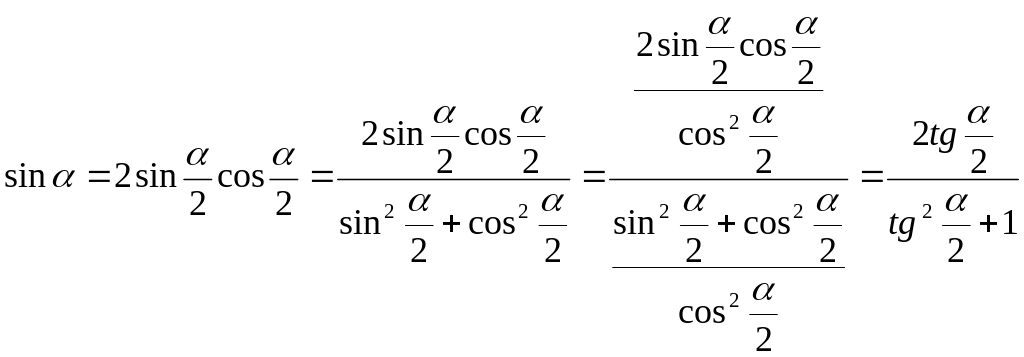
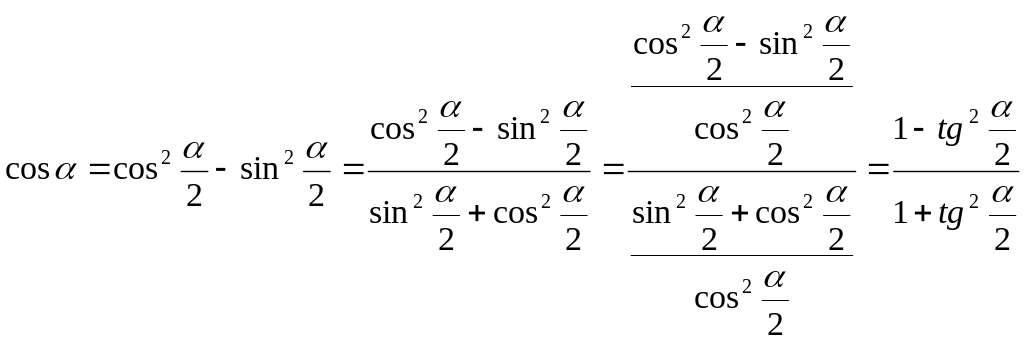
Примечание.
Формулы верны, если
![]() .
.
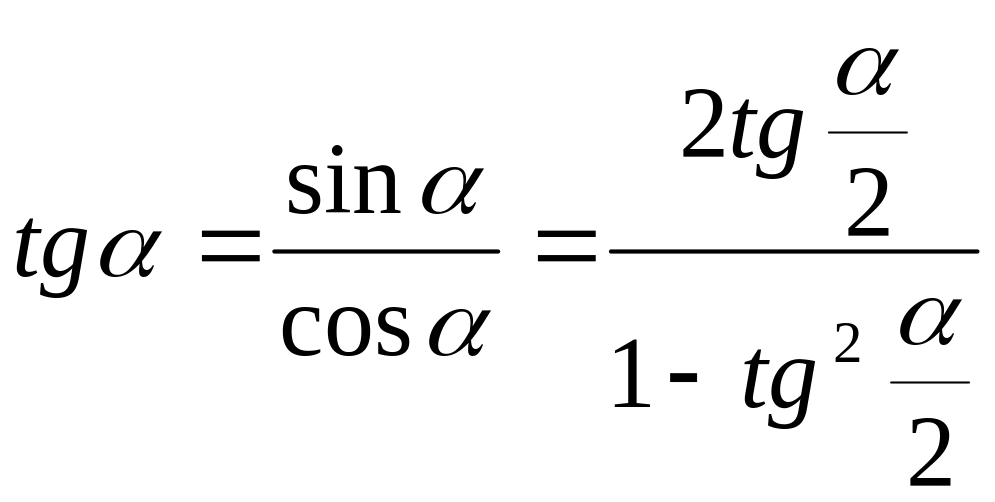
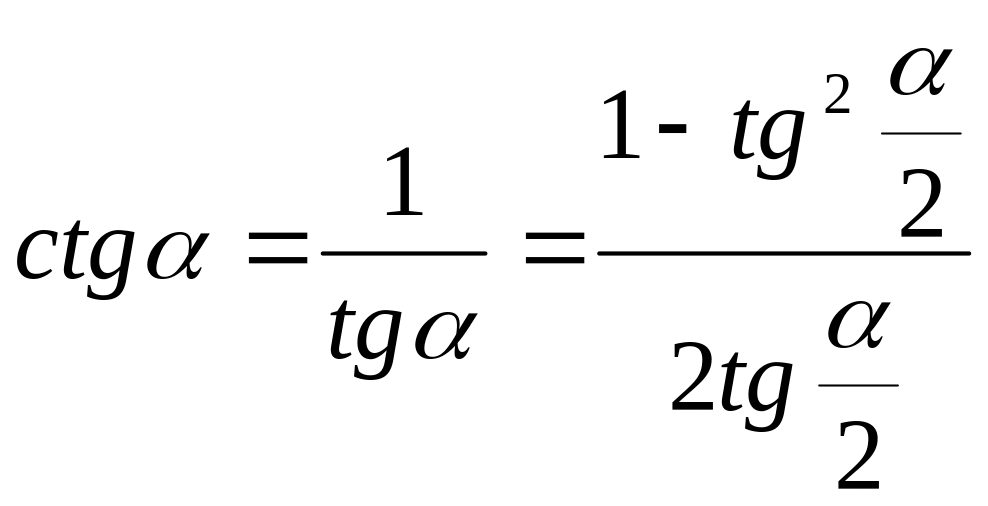
Пример:
Найти
![]() и
и
![]() ,
если
,
если
![]()