4. Распределение напряжений внутри массива грунта
4.1 Распределение напряжений по глубине торфяной залежи
Прочность, устойчивость сооружений и проходимость машин зависит не только от напряжений на поверхности залежи , но и от напряжений возникающих в нижележащих слоях, а также от свойств торфа в этих слоях от действия сил, приложенных на поверхности.
Торфяная залежь, как сложная многофазная водонасыщенная дисперсная система органического происхождения, при нагружении проявляет упруго – вязко – пластические свойства, которые описать точными аналитическими зависимостями сложно. Поэтому в задачу вводят упрощения, принимая торфяную залежь как линейно деформируемое упругое полупространство, для которого применимы решения Буссинеска о распределении напряжений от действия внешних сил. Это допущение предполагает, что между деформациями и напряжениями можно допустить линейную связь. Т.е. принять за основу закон Гука.
Это допустимо, когда величина напряжений под подошвой штампа не вызывает пластических деформаций.
Многочисленные исследования показали, что такой подход можно использовать (Корчунов с.с., Амарян Л.С., Силкин А.М. Миронов В.А. и др.)
Действие сосредоточенной силы
Сосредоточенная сила, это сила приложенная на поверхности перпендикулярно плоскости, ограничивающей полупространство, которое условно считается однородным по глубине и линейно-деформируемым.
В
озьмём
в глубине массива точку М, положение
которой определяется полярными
координатами: углом β и
радиусом R (рис. 1)
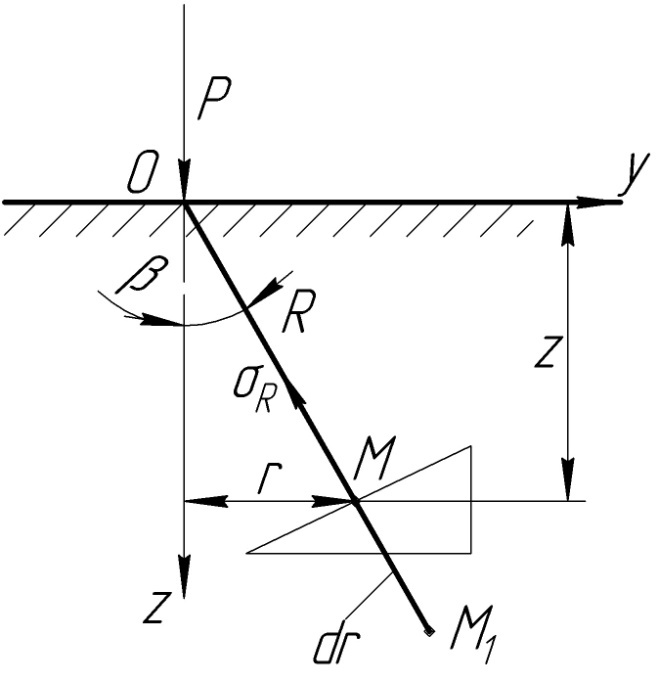
Рис 4.1 Действие сосредоточенной силы
Принимаем как постулат, что напряжение ϬR пропорционально Cos β и обратно пропорционально квадрату расстояния от точки приложения сосредоточенной силы R2 .(Закон всемирного тяготения).
ϬR
= А
, где А – коэффициент. А =
Для площадки перпендикулярной радиусу:
ϬR
= 
Cos β
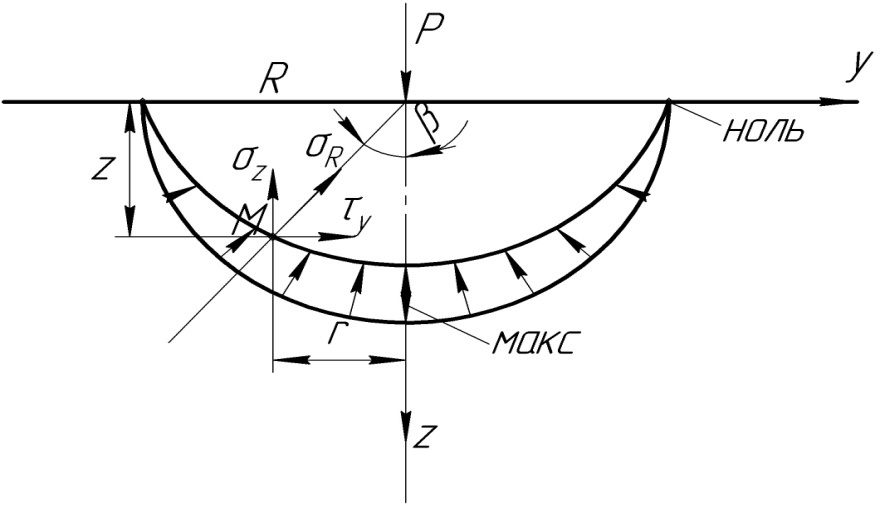
Рис 4.2 Действие сосредоточенной силы внутри шарового полупространства
Если величину радиальных напряжений отнести к площадке параллельной ограничивающей плоскости, то исходя из геометрических соображений,
= ϬR Cosβ
, то есть
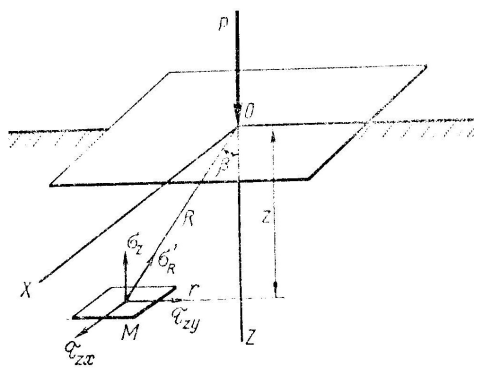
Рис 4.3 Составляющие напряжений для площадки параллельной ограничивающей плоскости
=
Разложив эту силу по осям координат X,Y,Z получим в окончательном виде:
ϬZ =
; τzy
=
, 
.
Величину сжимающих напряжений можно определить по формуле:
ϬZ
= K
,
где К – коэффициент, полученный после преобразования основной формулы и приводимый в таблицах исходя из соотношения R/z. [Цитович Н.А. Механика грунтов]
В случае пространственной задачи действуют как нормальные, так и касательные напряжения.
, Радиальное напряжение Ϭ R отнесенное к горизонтальной площадке
σ'R ` = σR cosβ или
σ'R = (3/2)·(Р/π)·(z²/R4 )
(если cosβ выразить через отношение z/R)
Проектируя величину Ϭ'R на три взаимно – перпендикулярные направления получаем составляющие напряжения для той же площадки, т.е. площадки параллельной плоскости, ограничивающей массив.
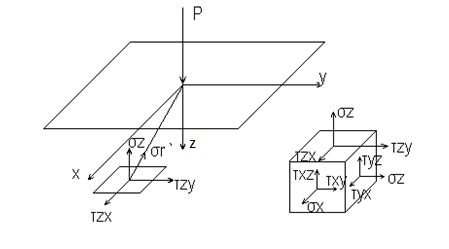
Рис 4.4 Составляющие напряжений по трем осям координат
σz = σr `cos(σr`ˆz) ; τzy = σr `cos(σr`ˆy); τzx = σr `cos(σr`ˆx)
cos(σr`ˆz) = z/R cos(σr`ˆy) = y/R cos(σr`ˆx) = x/R
окончательно получим:
σz = (3/2)·(P/π)·(z³/R³·R²)
τzy = (3/2)·(P/π)·(yz²/R³·R²)
τzx = (3/2)·(P/π)·(xz²/R³·R²)
По этим формулам можно определить составляющие напряжения от действия сосредоточенной силы для любых площадок параллельных ограничивающей плоскости.
Для определения вертикальной составляющей напряжения можно пользоваться более простой формулой:
Ϭ Z = k·P/z²
где k коэффициент, значение которого приводится в таблицах в зависимости от отношения r/z, где z – глубина от ограничивающей плоскости, а r – расстояние от оси z [Цитович Н.А. Механика грунтов.]
Всего в пространственной задаче девять составляющих напряжений, три нормальных и шесть- касательных. Причём касательные попарно равны между собой.