3.4. Структурно–фазовая деформируемость грунтов.

Отдельные компоненты (фазы) грунта по-разному сопротивляются силовым воздействиям и . по-разному деформируются. Поэтому состояние грунта в целом рассматривается как квазиоднородное (но одновременно изучается поведение отдельных фаз и их взаимодействие друг с другом).

Общая зависимость между деформациями и напряжениями.

- У сыпучих грунтов, при однократном нагружении, возникают необратимые смещения и повороты зерен относительно друг друга, что обусловливает его остаточную деформацию.

- У связных грунтов на характер деформирования влияют структурные связи, жесткие и вязкие. При жестких связях, когда нагрузка не превышает прочность связей, грунт деформируется как квазитвёрдое тело. При вязких водно – коллоидных связях, имеющих различную прочность, некоторые из этих связей начинают разрушаться (вязко течь) уже при небольших нагрузках, другие при больших и т.д. Это обусловливает непрерывное присутствие как обратимых, так и остаточных деформаций. При этом остаточные деформации по величине часто превосходят обратимые во много раз.

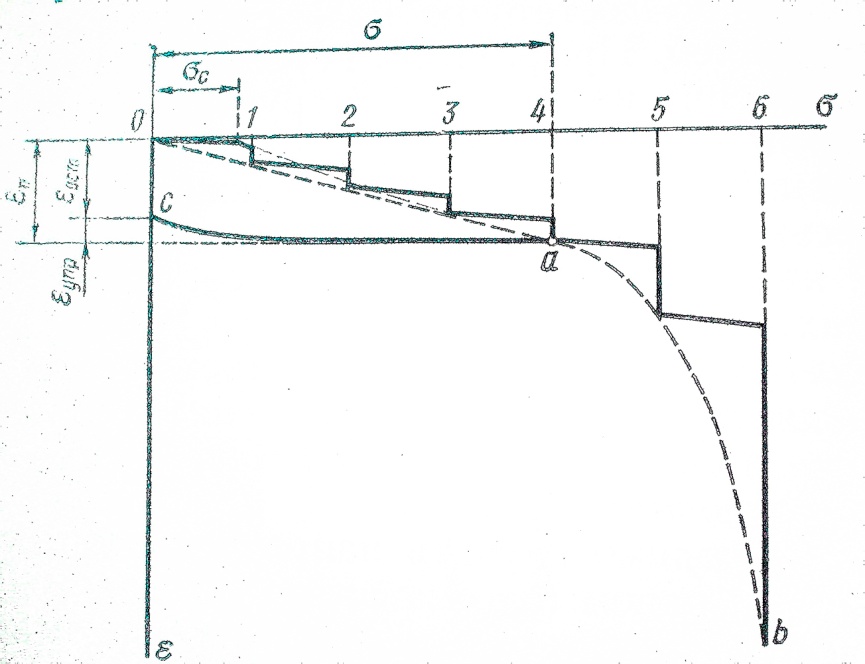
Рис 3.17 Кривая изменения деформации грунта в зависимости от величины нормальных напряжений

Ϭ = нормальные напряжения; ε = относительная деформация

Математически:

ε = α_С · Ϭ _С + (Ϭ_П – Ϭ_С )^m ,

где α_С и α_П - опытные коэффициенты; Ϭ_С - напряжения не превышающие прочность структурных связей;

Ϭ_П - Ϭ_С = Ϭ - действующее нормальное напряжение, обусловливающее деформацию грунта при частичном и полном разрушении структурных связей; m – параметр нелинейности (определяется экспериментально).

α _П = 1/Е,

где Е -модуль нормальной упругости

α _{П =} ,

где β -коэффициент бокового расширения; Е ₀ – модуль общей деформации; r –показатель степени (экспериментальный).

Если давление больше прочности структурных связей

ε = α _С.П Ϭ ^m ,

Где α _С.П - общий коэффициент пропорциональности,

α _С.П = β/Е ₀ .

Принцип линейной деформируемости

Зависимость ε = f (Ϭ) можно считать линейной, если изменения внешних давлений невелики ( 1 – 3 кг/см ² для неплотных и 5 -7 плотных грунтов, т.е. m = 0

ε = α_с.п · Ϭ _{(формула 1)}

В этом случае будут применимы решения теории упругости. Т.е. при небольших изменениях давления грунт можно рассматривать как линейно деформируемое тело.

m _υ = ,

где m _υ - коэффициент относительной сжимаемости (относительная осадка, приходящаяся на единицу действующего давления); S_i – полная осадка образца при i – той нагрузке; h – начальная высота образца; р_i – действующее давление.

Относительная деформация

ε = s/h, и m = ε/p_i , тогда

ε =m_υ p_i (формула 2)

приняв Ϭ = P и зная, что α_С.P = β/E₀ ._.

Сравнивая формулы 1 и 2, получим:

m _υ = β/E ₀ или E ₀ = β/m _υ

Примечание; для слабых грунтов, с несущей способностью менее 1 кг/см² , принцип линейной деформирования неприемлем.

Деформация отдельных фаз грунта

- для скелета грунта изменение напряженно – деформационного состояния зависит от времени из-за его ползучести под нагрузкой и от истории (т.е. от предыдущих нагрузок). Теория деформации скелета получила название теории наследственной ползучести

- для поровой жидкости. Деформация поровой жидкости, при отсутствии в ней газа, невелика и она может рассматриваться как идеально упругое тело.

- для пузырьков газа деформация отдельно не учитывается.

- смесь воздуха и воды должна учитываться в полной мере

m_w = (1 – J_w ) , где J_w - коэффициент водонасыщенности грунта; Р_а -атмосферное давление, кг/см² . J_w = (см. тему2)