Закон Кулона

1) для сыпучих грунтов

Кривая диаграммы предельных сопротивлений принимается за прямую линию (можно).

Предельное сопротивление сдвигу:

_{τi = Ϭ tg φ}

Где угол внутреннего трения;

tg - коэффициент внутреннего трения

tg - обычно обозначают как f (коэффициент трения), тогда

- Закон Кулона для несвязанных (сыпучих) тел, в которых сопротивление сдвигу есть сопротивление внутреннего трения.

2) Для связных грунтов.

Если грунт связный, то сопротивление сдвигу оказывают внутреннее трение и внутреннее сцепление.

Диаграмма предельных напряжений выглядит так:

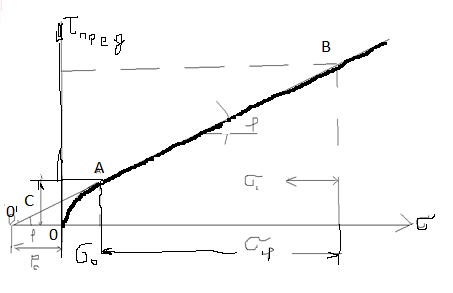
Рис 3.9 Диаграмма предельных напряжений

От «А» до «Б» прямая линия. Трение начнётся лишь тогда, когда будут преодолены силы внутреннего сцепления частиц. «С» и формула закона Кулона примет вид:

где с – суммарные силы сцепления в грунте

,

где, - структурное (жёсткое) сцепление, - пластичное сцепление, обусловленное водно-коллоидными связями,

по графику: , где - всестороннее давление в грунте, называемое давлением связанности,

Кривые предельных напряжений сдвига Мора:

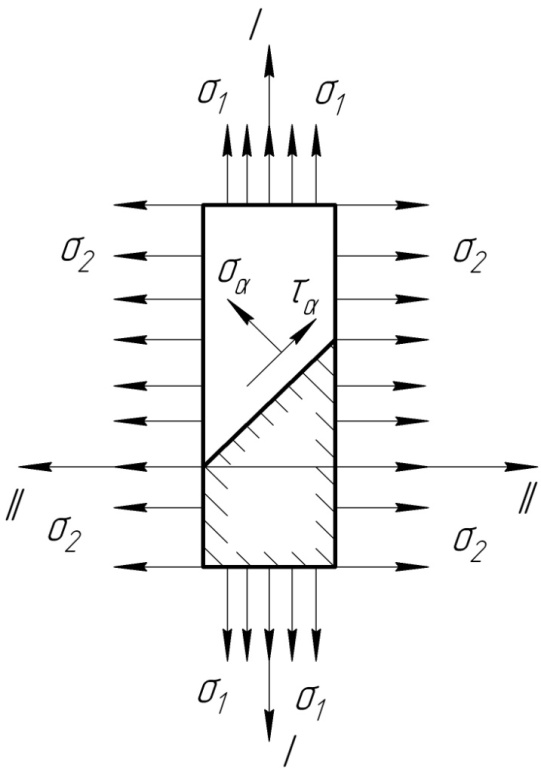
Рис 3.10 Схема напряженного состояния образца

Как известно, нормальные и касательные напряжения на сечениях, нормаль к которым составляет с наибольшим главным напряжением угол α, определяется равенством:

Вычисление значений и по этим формулам можно заменить простым и удобным построением кругов Мора

.

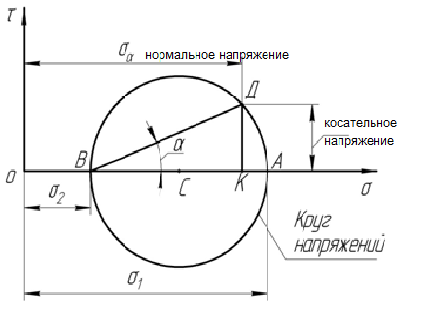
Рис 3.11 Схема построения Круга напряжений Мора

τ _α численно равна длине отрезка DK

Ϭ _α численно равна длине отрезка OK

По результатам определения максимального сопротивления грунта сдвигу можно построить диаграмму напряжений.

Для сыпучих грунтов.

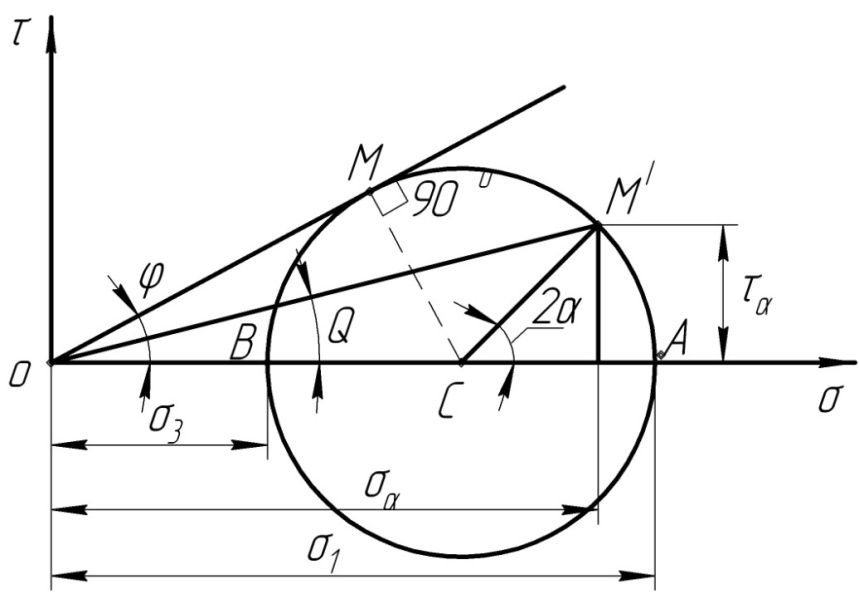
Рис 3.12 Круг напряжений Мора для сыпучих грунтов

Предельная прямая (ОМ) называется огибающей кривой, т.к.при рассмотрении семейства огибающих кругов она принимает форму кривой.

Если внутреннее сцепление C = 0, то

Для связных грунтов.

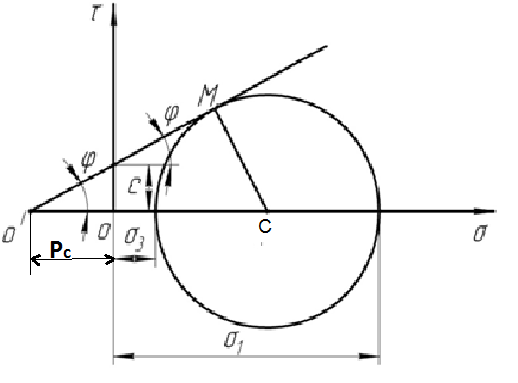
Рис 3.13 Круг напряжений Мора для связных грунтов

Где Р_С = С Сtq φ - давление связности.

Окончательно

Sinφ =

3) Для идеально связных грунтов

прочность определяется только удельным сцеплением, т.е.

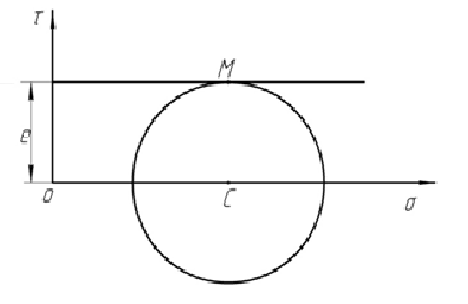
Рис 3.14 Круг напряжений Мора для идеально связанных грунтов

Круги Мора дают представление о присутствии определённых напряжениях в любой точке нагруженного грунта. При этом определяют экспериментально, а -это нормальная нагрузка.

Примечание: Ϭ ₁ , Ϭ ₂ ,Ϭ ₃ - главные напряжения, направленные вдоль главных осей координат в порядке от большего к меньшему.

Условно считается, что нарушение целостности материала зависит только от наибольших и наименьших главных напряжений, и мало зависит от средних. (экспериментально доказано, что так и есть, влияние средних не велико, и им пренебрегают). При этом вместо трёхмерного пространства (объём) получается двумерное (плоскость), что очень упрощает расчёты.

Обычно приходится иметь дело не со всей огибающей кривой, а с ее частью. Тогда ее заменяют прямой, касательной к кругам Мора.

Рис 3.15 Схема огибающей кривой

Принято изображать круги Мора в виде полукруга, а не окружности, т.к. обе половины симметричны.

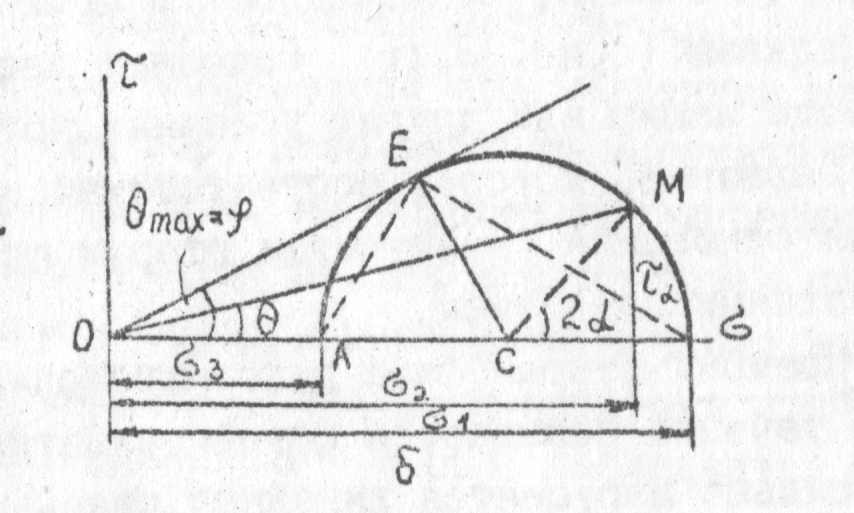
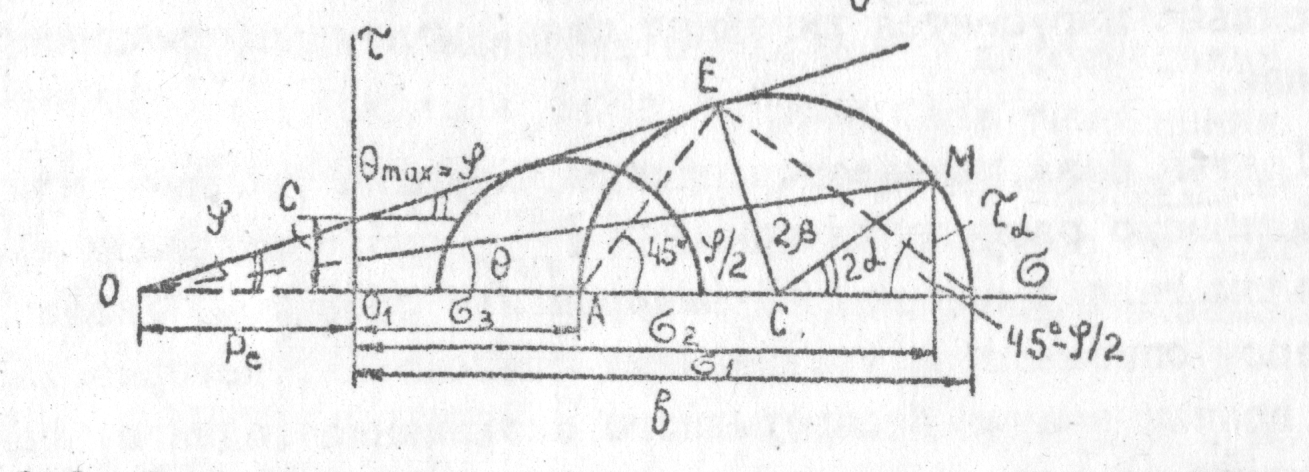
Рис 3.16 Обычное построение кругов напряжений Мора