7.3 Определение упругих деформаций.
Используют оба метода определения деформаций: 1) Метод общих упругих деформаций и 2) Метод местных (не выходящих за периметр штампа) деформаций.
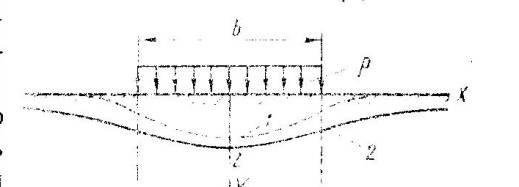
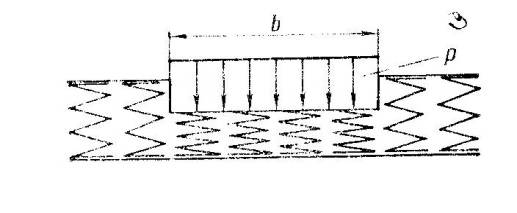
Рис 7.1 Схема действия нагрузок при расчетах по общим упругим деформациям (сверху) и по местным деформациям (снизу)
Определение общих упругих деформаций базируется на теории упругости для упругого полупространства. Используется формула Буссинеска:
Sz=P/(πCR) ,
где С=Е/(1+μ2) –коэффициент упругого полупространства; Р - сосредоточенная сила
Осадки точек полупространства определяют путем интегрирования элементарных вертикальных перемещений по площади F от элементарной сосредоточенной силы.
Экспериментальная проверка этого метода дает хорошие результаты. В конечном итоге деформация прямо пропорциональна площади F и давлению Р.
где А - пост. величина осадки под жестким штампом, определяемая по уравнению Шлейхера. Тогда:
S=(1- μ2)wpb/E ,
где w-коэффициент формы и жесткости штампа; b- ширина или диаметр штампа; Е-модуль упругости или деформации основания; μ- коэффициент Пуассона или бокового расширения. (w=0,85-1,7; круг = 0,85; квадрат = 0,95; при L/b=1,5 w=1,15; L/b=4 w=1,7) ; (слаборазложившийся: μ=0,25-0,35 ; среднеразложившийся: μ =0,35-0,45 ; сильноразложившийся: μ=0,45)
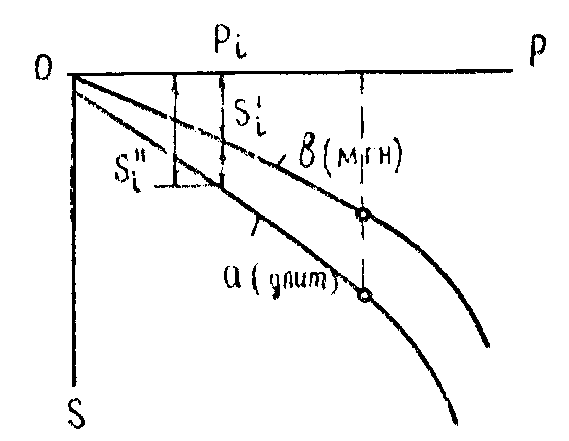
Рассматривая протяженность процесса осадки во времени необходимо учитывать изменение деформации во времени и определить модуль деформации в соответствии с ним
Рис 7.2 Зависимость осадки штампа при длительном и быстром нагружении
1- S=f(p) –при быстром нагружении
2- S=f(p) –при медленном нагружении
Е=(1- μ2 )Рwb/S
При подвижных кратковременных нагрузках (проезд машины) определяют условно мгновенный модуль деформации (t=2-3 мин.) . Мгновенный модуль упругости зависит от пористости и влажности торфа и может быть определен при помощи испытаний на сдвиг по крыльчатке
По методу местных упругих деформаций по гипотезе Фусса-Винклера
(давление прямопропорционально местной упругой осадке
P=Cz*Z Z=P/Cz
P - удельное давление ,кг/см2 Z –вертикальная упругая осадка; Сz - коэффициент. упругости основания (коэффициент постели)
7.4.Одномерное компрессионное уплотнение торфа и торфяной залежи
Процесс идет без бокового расширения. За счет отжатия поровой жидкости, сжатия и удаления газовой фазы. Объем твердой фазы остается постоянным ( его уплотнение ничтожно мало). Объем газа (0,5-3%) т.е. мал и им можно пренебречь. Главную роль при уплотнении играет объем жидкой фазы, форма и размеры микропор. В торфах самыми водонасыщенными элементами являются грубодисперсные волокнистые фракции с размерами более 250 мкм. В микропорах содержится иммобилизованная вода и защемленные пузырьки воздуха. Крупные частицы окружены и насыщены гуминовыми и глинистыми гелями тонкодисперсной фракции, что сильно осложняет процесс деформации в физическом смысле. Таким образом торф при уплотнении и разуплотнении следует считать сложным, обладающим упруго- вязко- пластичными свойствами, грунтом. Гидравлический радиус пор изменяется от 0,5 до нескольких десятков мкм. и сильно уменьшается в процессе уплотнения. Это свидетельствует о высокой подвижности поровой жидкости при внешнем давлении. Содержание влаги в торфе при невысоких давлениях (менее 5кг/ см2) достигает определенной критической величины (Wкр.1=190-230% ) после чего процесс отжатия ее при уплотнении протекает значительно медленнее. Каждой уплотняющей нагрузке соответствует своя равновесная влажность. По ней можно судить о мере уплотнения торфа.
Процесс сжатия торфа описывается не логарифмической, а экспоненциальной зависимостью
λ= λmax(1-е1-M P) или е=еmin +е е1M Р
где е-коэф. пористости; е1 –осн. натурального логарифма.
Параметры λmax и М можно установить по прямолинейной зависимости:
Δ λ/ ΔР=f(λ).
Ориентировочно М = 1,5 , λmax = 0,9; 0,8; и 0,65 для слабо, средне и сильно разложившегося торфа соответственно.
Л.С.Амарян предложил интерпретировать Δ λ/ ΔР = f (λ) как а0 =Δ λ/ ΔР),
где а0 –коэффициент относительной сжимаемости, широко используемый при испытаниях грунтов.
Зависимость а0 =f(Р) является параболической, поэтому зависимость а0i от λi можно представить в виде линейной с пределами зависящими от физических характеристик торфа.
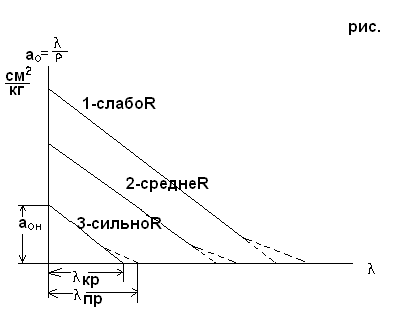
Рис 7.3 Зависимость а о от относительной деформации для торфов различной степени разложения (R)
Уравнение коэффициента относительной сжимаемости :
а0i = а0н -к λi , где
а0н –начальный коэф. сжимаемости , к= а0н / λкр – коэф. пропорциональности.
Т.к. а0i = λi/Pi, то относительная деформация λi, соответствующая ступени нормального давления Рi будет:
λi = Рi*а0i /(1+K*Рi)
Величина конечной осадки уплотняемого слоя начальной толщины h0 с учетом λ=Si/ h0 будет:
Si = Pi а0i h0 /(1+K*Рi)
Зная что Екi = Eн + Р tgά , можно установить текущее значение модуля деформации Екi = Рi / λi т.е.
Екi = (1+KР)/ аон
При Р→0, Ек→Ен, Екi =1/аон
Это соответствует грунту при отсутствии внешней нагрузки с начальным коэффициентом пористости е0 .
Т.о. процесс уплотнения торфа сводится к установлению параметров аoн и К которые можно определить, зная что
аон=m(е0-еkp`)
где m- константа, е0 устанавливается расчетом по значениям W,γ,γd, известным или найденным опытным путем. Тогда в уравнении остается неизвестным значения еkp` т.е.коэффициента пористости торфа после отжатая из него всей свободной, энергетически не связанной с твердой фазой влаги (характеризуется первым критическим влагосодержанием Wkp`).
С учетом плотности скелета γd и воды γw
е кр 1 = (γ d / γ w ) W кр1
В этом состоянии грунт не содержит газовой фазы и находится в 2-х фазном состоянии.
К = а он / λ кр1
λ кр1 =( е 0 – е кр1 )/(1+ λ 0 )
В практике торфяного производства оперируют давлениями не превышающими 1- 2 кг\см2 , поэтому вполне можно ограничиваться линейным участком на графике а0=ƒ(λ) ( рис 7.3) - λkp.
К = а он / λ кр1 = m(1+e 0 ), где а он = m(e o – e кр1 )
То есть основные параметры уравнения одномерного уплотнения органоминеральных грунтов aoн и к зависят от начального ( е0 ( и конечного(еkp`) коэффициентов пористости. [ См. уравнение: aoi=aoн-kλi]
Расчет конечной осадки S органического слоя торфяного грунта толщиной h0 при заданном давлении P можно свести к определению W,γ , γd и е0.
е о = (1/γ) γ d (1+w) - γ