
- •Краткое содержание
- •Введение
- •2 Свойства торфа и торфяных залежей
- •2.1 Общетехнические свойства торфа Классификация грунтов по происхождению
- •2.2 Физико-механические свойства торфов
- •2.3 Связь между основными показателями физико-механических свойств торфа
- •2.3 Показатели свойств различных торфов
- •3. Основные закономерности механики грунтов
- •3.1. Закон уплотнения грунтов
- •3.2.Водопроницаемость грунтов
- •Эффективное и нейтральное давление.
- •Полное давление в водонасыщенном грунте:
- •3.3. Контактное сопротивление сдвигу .Условия прочности
- •Закон Кулона
- •3.4. Структурно–фазовая деформируемость грунтов.
- •Общая зависимость между деформациями и напряжениями.
- •Принцип линейной деформируемости
- •Деформация отдельных фаз грунта
- •4. Распределение напряжений внутри массива грунта
- •4.1 Распределение напряжений по глубине торфяной залежи
- •Действие сосредоточенной силы
- •Сжимающее напряжение от нескольких сосредоточенных сил
- •Действие силы, приложенной внутри линейно-деформируемого пространства
- •Действие равномерно распределенной нагрузки
- •Определение сжимающих напряжений по методу угловых точек.
- •Определение сжимающих напряжений по способу элементарного суммирования
- •4.2 Распределение напряжений при полосообразной нагрузке в линейно деформируемом массиве. Плоская задача.
- •4.3 Распределение давлений по подошве тел. Контактная задача.
- •4.4 Распределение напряжений от собственного веса грунта
- •5. Лабораторные методы определения механических свойств торфа
- •5.1.Компрессионные испытания.
- •5.2 Испытание торфа на сдвиг (срез).
- •5.3 Трехосные испытания торфа
- •6. Полевые методы испытаний торфяной залежи
- •6.1. Основные положения
- •6.2. Метод вращательного среза
- •6.3. Полевые испытания торфяных залежей методом статического зондирования
- •6.4. Измерение порового давления в слабых грунтах
- •6.5. Несущая способность залежи и проходимость машин (штамповые испытания)
- •6.6. Исследование осадок торфяных оснований под насыпями
- •7. Деформационные свойства торфяных залежей
- •7.1 Виды деформаций торфяной залежи
- •7.2 Распределение деформаций по глубине торфяной залежи
- •7.3 Определение упругих деформаций.
- •7.4.Одномерное компрессионное уплотнение торфа и торфяной залежи
- •7.5 Консолидация (Одномерное уплотнение торфа во времени)
- •8. Предельно - напряжённое состояние торфяной залежи
- •8.1 Фазы напряжённого состояния торфяной залежи
- •8.2 Фазы напряжённого состояния торфяной залежи при полосообразной нагрузке
- •1) Первая фаза (первое предельное давление
- •2) Вторая фаза (второе предельное давление )
- •Оценки устойчивости откосов по методу круглоцилиндрических поверхностей.
- •9.2 Разрушение грунта в придонной зоне канала и выпор грунта.
- •10.Изменение физических свойств грунтов при промерзании.
- •10.1 Мёрзлые грунты
- •10.2 Физические свойства мерзлых грунтов.
- •10.3 Прочность торфа и торфяной залежи при промерзании
- •Приложения Приложение 1.
- •Литература
- •Оглавление
- •2 Свойства торфа и торфяных залежей 4
- •3. Основные закономерности механики грунтов 11
- •4. Распределение напряжений внутри массива грунта 25
- •5. Лабораторные методы определения механических свойств торфа 38
- •6. Полевые методы испытаний торфяной залежи 45
- •7. Деформационные свойства торфяных залежей 56
- •9. Устойчивость откосов каналов и выпор торфа. 67
- •10.Изменение физических свойств грунтов при промерзании. 71
Определение сжимающих напряжений по способу элементарного суммирования
Используют в случае, когда площадь загрузки нельзя разбить на прямоугольники.
Загрузочную площадь разбивают на площадки такой формы, чтобы было удобно считать приходящуюся на них нагрузку сосредоточенной в центре тяжести их поверхности.
Сжимающее напряжение по способу элементарного суммирования определяется по формуле
Ϭz = ∑Ki![]()
где Ki коэффициент, определяемый по таблице (Цытович МН Механика грунтов).в которой r -проекция на горизонтальную плоскость расстояния от центра тяжести i- го элемента до точки м; z – глубина.

Рис 4.10 Схема разбивки загруженной площадки
Разбиваем загруженную площадь на 6 элементов : 4 квадрата 1х1 м и 2 треугольника с катетом по 1 м. Принимаем, что в центре каждого элемента приложена сосредоточенная сила Рi=pFi.,где F – площадь элемента.
Определить расстояние r для квадратов: r1=r2=r3=r4=0.71м;
для треугольников: r5=r6=1,37м
4.2 Распределение напряжений при полосообразной нагрузке в линейно деформируемом массиве. Плоская задача.
Задача о распределении напряжений в линейно деформируемом массиве в ряде случаев упрощается, если ее удаётся свести к плоской задаче , т. е. к такому состоянию, когда напряжения распределяется в одной плоскости и не зависят от координат перпендикулярных рассматриваемой плоскости. Это условие применимо для очень вытянутых в плане сооружений, например ленточных фундаментов , оснований подпорных стенок , дамб. (Это, так называемый, случай погонной нагрузки). Для таких сооружений во всех сечениях по длине, кроме краевых участков, распределение напряжений будет одинаковым.
а) От действия равномерно распределенной нагрузки

Рис 4.11 Действие равномерно распределённой нагрузки
α угол видимости
β = α/2 + β’, где β’ – угол составленный крайним лучом с вертикалью.
Формулы 1:
Ϭz=P/π ( α +sinα cos2β)
Ϭy= P/π ( α –sinα cos2β)
Ϭy= P/π (sinα cos2β)
Заменив всё, кроме Р коэффициентами, получим:
Формулы 2:
Ϭz= Kz P
Ϭz= Ky P
Ϭz= Kyz P
коэффициенты Kz, Ky, Kyz приведены в таблице в зависимости от отношения z/b и y/b (ЦитовичМН Механика грунтов)
При помощи таблицы можно рассчитать распределение напряжений по горизонтальным и вертикальным сечениям массива ( случае плоской задачи).
б) Эпюры распределения сжимающих напряжений Ϭz
В вертикальных сечениях
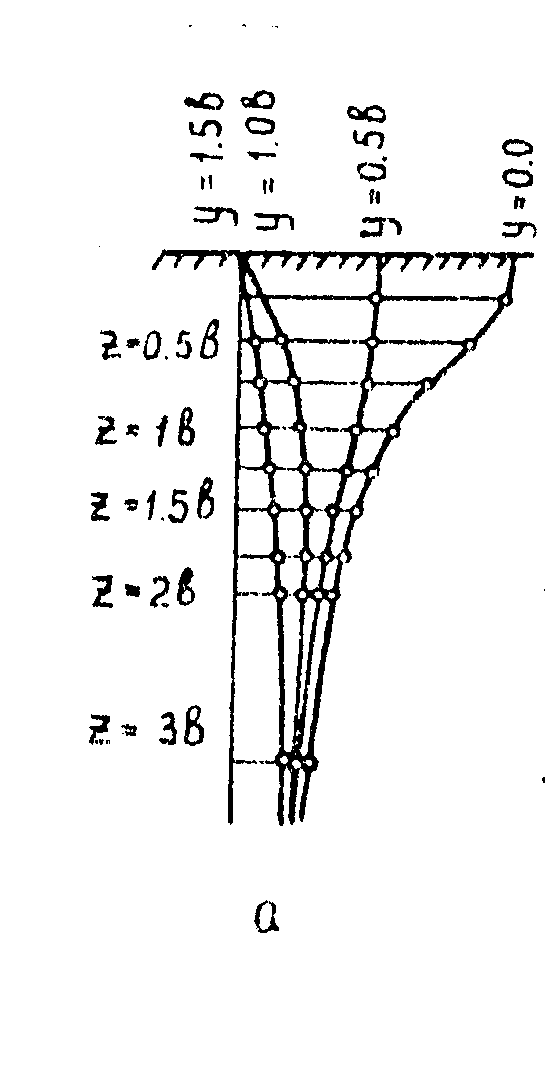
Рис 4.12 Эпюры сжимающих напряжений в вертикальных сечениях массива
В горизонтальных сечениях
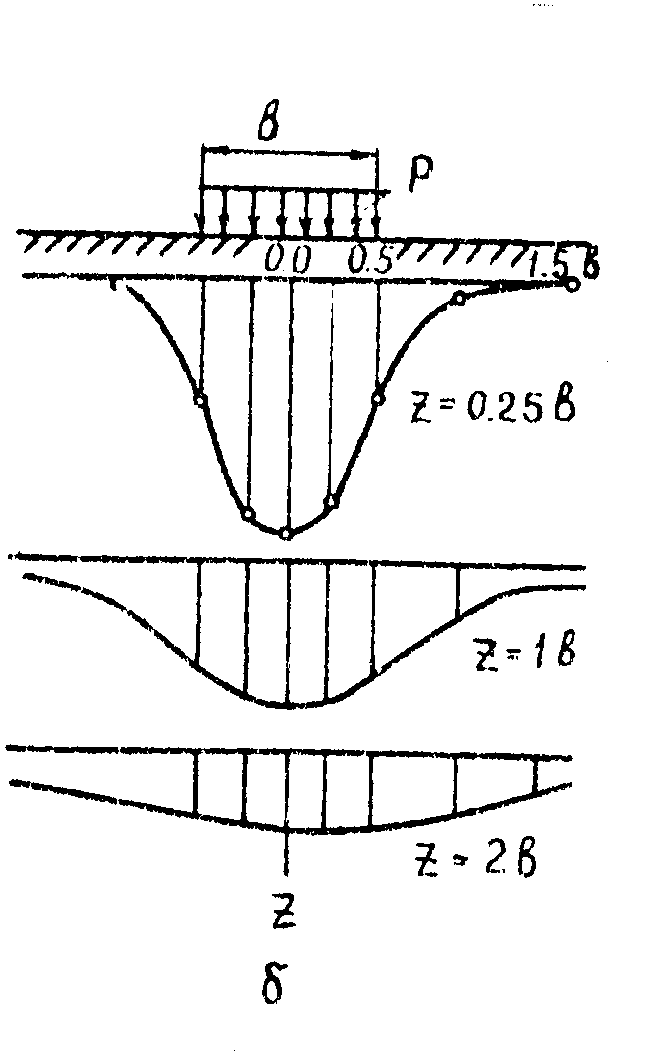
Рис 4.13 Эпюры сжимающих напряжений по горизонтальным сечениям
Линии равных напряжений( изобары)
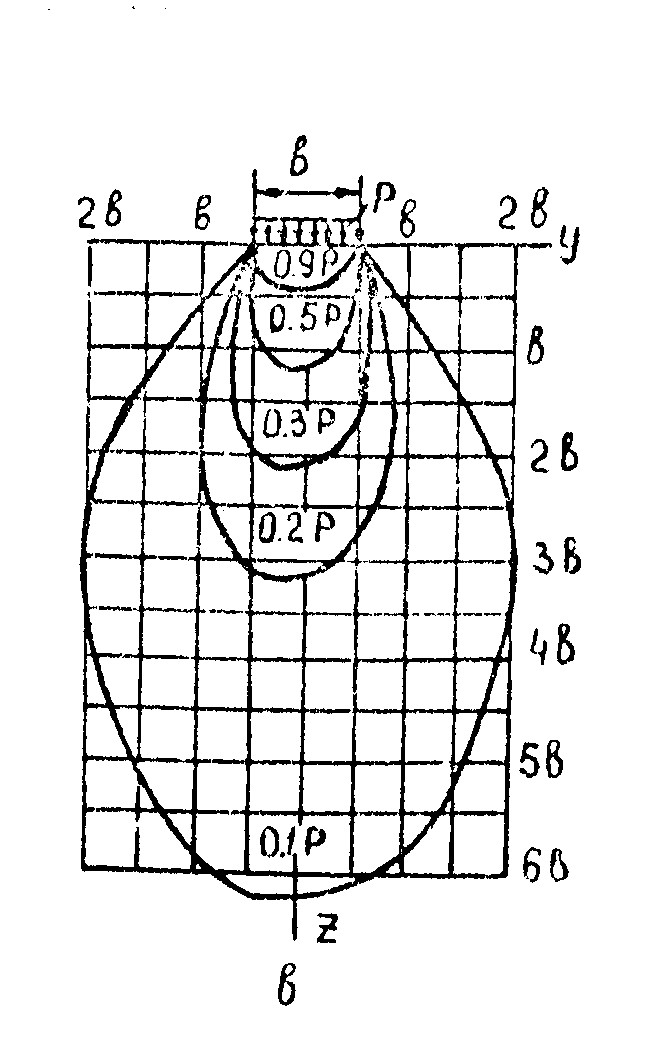
Рис 4.13 Изобары– линии одинаковых вертикальных сжимающих напряжений или давлений в долях от Р ( интенсивности линейной нагрузки)
Эпюры горизонтальных напряжений (распоры)

Рис 4.14 Распоры (Ϭ y ) - линии одинаковых горизонтальных напряжений
Эпюры сдвиговых напряжений
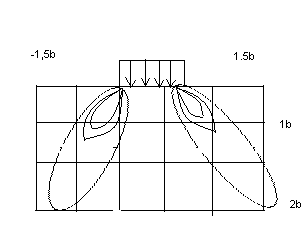
Рис 4.15Сдвиги (τzx ) – линии одинаковых касательных напряжений
Сжимающие напряжения в случае плоской задачи, распространяются на большую глубину, чем в случае пространственной задачи.
Область распределения распоров выдвигается в стороны более чем на ширину подошвы полосообразной нагрузки.
Максимальные сдвигающие напряжения имеют место под краями подошвы полосообразной нагрузки. По оси нагрузки сдвиги равны нулю.
