Энергоснабжение

Глава 1.

ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА.

1.1. Основные понятия и определения термодинамики

Продукты сгорания топлива называется теплоносителем. Вода и пар называются рабочим телом. Процесс переноса тепловой энергии от теплоносителя к рабочему телу называется теплообменом.

Термодинамика – наука о законах превращения тепловой энергии в механическую.

Термодинамическая система – это совокупность тел способных обмениваться энергией и веществом.

Термодинамическая система, которая не может обмениваться теплотой с другими системами называется теплоизолированной или адиабатно изолированной. Равновесное состояние системы называется стационарным, неравновесное – нестационарным.

Количественное состояние системы характеризуется параметрами состояния: давлением Р, температурой Т, объемом V. Они не зависят от размеров и массы системы и называются интенсивными, обозначается малыми (строчными) буквами.

Термодинамические параметры, пропорциональные количеству вещества или масса системы называется экстенсивными, это объем V, масса М, внутренняя энергия U и др. Экстенсивные параметры состояния обладают свойством аддитивности (складываемости) и записываются прописными буквами.

Абсолютное давление представляет собой результат воздействия молекул на стенки оболочки. Абсолютное давление, создаваемое воздухом называется барометрическим В.

Давление выше барометрического изменяется манометрами, ниже – вакуумметрами.

Приборы показывают разность между абсолютным и барометрическим давлением, т.е. избыточное или вакуумметрическое.

Барометрическое давление изменяется, поэтому

если P>B если P>B Измеряется в Па, 1Па = 1 Н/м2 1 бар = 105 Па 1 атм = 98 · 103 Па 1 мм рт. ст = 133,3 Па

Температура – это степень нагретости тела, измеряется в Кельвин (К)

Удельный объем – объем единицы массы вещества

Масса вещества в единице объема называется плотностью

Связь между параметрами состояния характеризуется диаграммой состояния.

Изменение состояния рабочего тела под действием окружающей среды называется процессом.

При перемещении поршня в цилиндре объем, температура, давление газа непропорционально меняется. Если при этом температура и давление по всему объему газа одинаковы, то такой процесс называется равновесным.

Термодинамические процессы при неизменном значении какого либо параметра называются изопроцессами (рис. 1.1).

Рис. 1.1. Изопроцессы: изохорные АС, изобарные АД, изотермические АВ, адиабатные АЕ

Процессы: 1) при неизменном объеме –

- изохорные (линия АС);

2) при неизменном давлении –

- изобарные (линия АД);

3) при неизменной температуре –

- изотермическими (линия АВ)

4) без отвода и подвода теплоты –

- адиабатными (линия АЕ).

Равновесные термодинамические процессы обратимы, т.е. процесс может быть проведен от А к В и от В к А через точки 1, 2, 3, т.е. рабочее тело и окружающая среда пройдут через те же промежуточные состояния и в первом и втором случаях.

При нарушении этих условий процесс является термодинамически необратимым.

1.2. Основные законы идеального газа.

Уравнение состояния газа Клапейрона:

(1.1)

где R – газовая постоянная

различна для разных газов.

Из уравнения Клапейрона следует, что:

1. при постоянном давлении удельный объем изменяется прямо пропорционально изменению абсолютных температур;

2. при постоянном удельном объеме абсолютное давление газа изменяется прямо пропорционально изменению абсолютных температур;

Закон Авогадро: в равных объемах различных газов при одинаковых давлениях и температурах содержится одинаковое количество молекул. Плотности газов при одинаковых давлениях и температурах пропорциональны их молекулярным массам

- молекулярная масса

- плотность

Молекулярная масса - количество кг газа, равное числу единиц в молекулярном весе.

Молем (киломолем) газа называется масса газа, кг, равная его молекулярной массе.

Моль – это молекулярная масса газа.

Объем моля (киломоля) различных газов при аналогичных физических условиях одинаков.

Объем киломоля всех газов при нормальных физических условиях (НФУ) – р=760 мм рт. ст.=101,3 кПа, t=0⁰С, g=9,81 м/с² равен

Умножив уравнение Клапейрона на массу М получим уравнение состояния для произвольной массы идеального газа.

(1.2)

Умножив (1.1) на молекулярную массу получим уравнение Клапейрона-Менделеева для идеального газа для 1 кмоль его молекулярной массы:

, (1.3)

где – универсальная газовая постоянная для НФУ

Зная можно найти газовую постоянную любого газа по значению его молекулярной массы

Давление смеси газов равно сумме парциальных давлений отдельных компонентов смеси:

(1.4)

Парциальным называется давление компонента, которое он создавал бы находясь один в объеме, занимаемом смесью, при температуре смеси.

Для газовой смеси массой М уравнение состояния имеет вид:

(1.5)

- газовая постоянная и молекулярная масса смеси.

Массовая доля компонента:

(1.6)

Объемная доля компонента

(1.7)

Кажущаяся молекулярная масса смеси

(1.8)

Если объем смеси и объем компонента одинаков, температуры смеси и компонента одинаковы, давления разные, то они находятся по вышеизложенной формуле.

(1.9)

Для реальных газов уравнение Менделеева-Клапейрона имеет вид:

(1.10)

где - коэффициенты, зависящие от природы газа и учитывающие силы межмолекулярного взаимодействия и объем молекул.

В идеальном газе молекулы – точки, в реальном моделируются шарами. Коэффициент учитывает уменьшение объема за счет объема молекул и промежутков между ними.

Коэффициент учитывает притяжение молекул друг к другу и увеличение давления за счет сил межмолекулярного притяжения.

1.3. Первый закон термодинамики.

Термодинамическим процессом называется переход термодинамической системы (рабочего тела) из одного состояния в другое в результате его взаимодействия в внешней средой.

Равновесным называется такое состояние системы, когда ее параметры во всех точках имеют одинаковые неизменные значения.

Равновесным процессом называется процесс, характеризующийся непрерывной последовательностью равновесных состояний системы.

Равновесный процесс, который может быть осуществлен в прямом и обратном направлениях через ряд равновесных состояний называется обратимым процессом.

Теплоемкость с

массовая , объемная , киломольная

Теплоемкость зависит от температуры

- коэффициенты, приведены в справочниках.

Количество теплоты (тепловой энергии), необходимое для нагревания 1 кг газа от t₁ до t₂ определяется по выражению:

(1.11)

Теплоемкость газообразных веществ зависит также от внешних условий, при которых подводится и отводится теплота.

При изохорном процессе объем остается постоянным, т.е. он не совершает работы против внешних сил.

При изобарном нагреве газ, расширяясь, преодолевает внешнюю силу, например перемещает поршень, совершает работу. В этом случае для нагрева газа до одинаковой температуры потребуется большее количество тепловой энергии, чем при изохорном нагреве.

Удельная теплоемкость смеси равна сумме произведений удельных теплоемкостей отдельных компонентов на их массовые или объемные доли:

(1.12)

Внутреннюю энергию рабочего тела составляют кинетическая энергия тепловых движений молекул и колебательные внутримолекулярные движения атомов, а также потенциальная энергия взаимодействия молекул.

U – внутренняя энергия.

Для системы, находящейся в состоянии равновесия полная энергия системы Е равна ее внутренней E=U.

Внутренняя энергия зависит от температуры и объема U=f (T,V)

Изменение внутренней энергии

, (1.13)

где U₁,U₂ – внутренняя энергия соответственно в начале и конце процесса.

Если , то работа расширения равна 0 и все количество подведенной теплоты q расходуется на увеличение внутренней энергии:

при

При изменении объема при расширении рабочего тела совершается механическая работа – положительная механическая работа.

При сжатии рабочего тела работа производится со стороны внешней среды и считается отрицательной.

Рассмотрим газ, находящийся в цилиндре под поршнем.

Рис. 1.2. Перемещение поршня и изменение давления и объема рабочего тела

Поршень перемещается из т.1 в т.2

Площадь фигуры 1' 1 2 2' равна (работа Дж/кг).

Если dV>0 работа положительна, dV<0 работа отрицательна.

Первый закон термодинамики

Вся тепловая энергия (теплота), подведенная к системе, расходуется на изменение ее внутренней энергии и на совершение работы.

(1.14)

или

dq > 0 положительная теплота;

dq < 0 отрицательная теплота.

1.4. Термодинамические процессы идеальных газов.

1. Политропный процесс – изменяются параметры рабочего тела при постоянной теплоемкости и отсутствии движения.

2. Изохорный процесс – процесс, протекающий при постоянном объеме рабочего тела.

3. Изоборный – процесс, протекающий при постоянном давлении рабочего тела.

4. Изотермический – процесс, протекающий при постоянной температуре рабочего тела.

5. Изоэнтальпийный или адиабатный –процесс, протекающий без теплообмена между рабочим телом и внешней средой.

I. Изохорный процесс

Пример: охлаждение и нагревание

газа в в герметичном сосуде.

Рис. 1.3. Изохорный процесс в PV – диаграмме

График – изохора

, Поделим 1-е уравнение на 2-е:

Давление изменяется прямо пропорционально температуре газа.

Уравнение 1-го закона термодинамики

В изохорном процессе вся подведенная теплота идет на увеличение внутренней энергии.

(1.15)

II. Изобарный процесс.

Рис. 1.4. Изобарный процесс в PV – диаграмме

Пример: процесс нагревания воздуха в негерметичном помещении.

График – изобара.

Из уравнения состояния газа следует:

Объем газа изменяется прямо пропорционально его температуре.

В изобарном процессе теплота, подведенная к рабочему телу,

расходуется на изменение внутренней энергии тела и на

совершение работы.

или

т .к. и т.е.

универсальная газовая

постоянная

Если принять, что , то R это работа, производимая 1 кг газа при его нагревании на 1⁰С в изобарном процессе.

(1.16)

или

Энергию, равную сумме внутренней энергии и произведение давления на объем называют энтальпией.

, Дж (1.17)

III. Изотермический процесс

Рис. 1.5. Изотермический процесс в PV – диаграмме

График – изотерма

Процесс 1-2 – изотермическое расширение газа;

Процесс 2-1 – изотермическое сжатие газа.

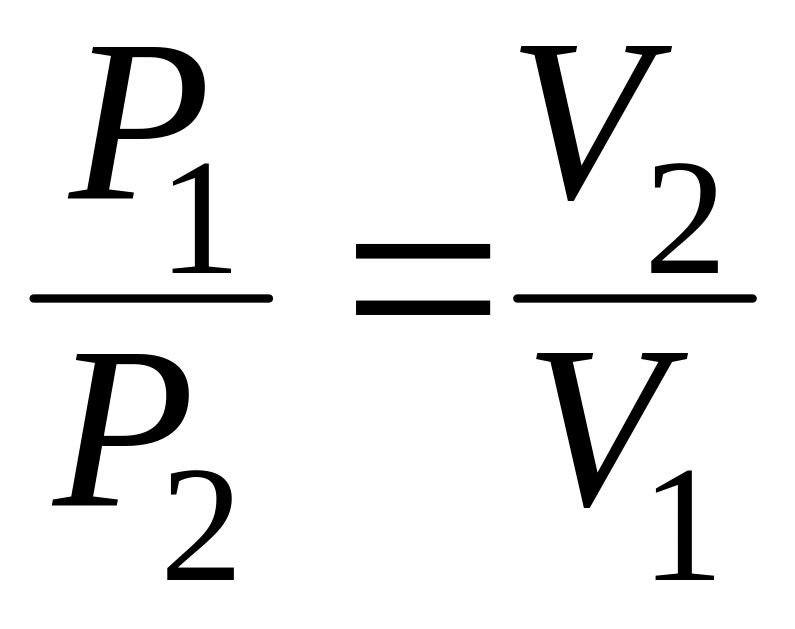(1.18)

Отношение абсолютных давлений обратно пропорционально отношению объемов.

(1.19)

Вся теплота, подведенная к газу в изотермическом процессе, расходуется на совершение механической работы.

(1.20)

т.к.

IV. Адиабатный процесс.

Процесс, осуществляющийся без подвода и отвода теплоты, т.е. dq=0, q=0.

Практически адиабатный процесс происходит при расширении или сжатии газа в цилиндре и протекающий настолько быстро, что теплообмен с окружающей средой не успевает произойти.

(1.21)

Следовательно, работа в процессе адиабатного расширения осуществляется за счет изменения внутренней энергии рабочего тела.

(1.22)

Уравнение адиабаты

(1.23)

где - показатель адиабаты

График – адиабата – неравнобокая гипербола, более крутая, чем изотерма.

Рис. 1.6. Адиабатный процесс в PV – диаграмме.

V. Политропный процесс.

В политропных процессах происходит изменение всех параметров.

Уравнение политропных процессов:

n – постоянная для данного процесса величина – показатель политропы с значением от 0 до ± .

Все рассмотренные термодинамические процессы являются частными случаями политропных процессов:

n =0, изобарный процесс

n =1, изотермический процесс

n =k, адиабатный процесс

n =± , изохорный процесс

Для политропного процесса:

, , (1.24)

(1.25)

1.5. Второй закон термодинамики. Цикл Карно.

Циклом называется последовательность определенных термодинамических процессов, в которых рабочее тело, протерпев ряд изменений, возвращается в первоначальное состояние.

В основу расчета тепловых двигателей положены идеальные круговые процессы, циклы. Процесс подвода теплоты в идеальных циклах рассматривается без изменения химического состава рабочего тела. В реальных циклах процесс подвода теплоты происходит в процессе сжигания топлива и рабочим телом в двигателях внутреннего сгорания являются продукты, образующиеся при горении.

Процесс отвода теплоты в идеальных циклах предусматривает наличие холодильника. В реальных циклах этот процесс осуществляется выпуском отработавшего рабочего тела в атмосферу. Процессы расширения и сжатия в реальных циклах сопровождаются теплообменом и не могут точно соответствовать адиабатным.

а) б)

Рис. 1.7. Круговой цикл в РV – диаграмме

На круговом цикле (рис. 1.7, а) на участке 1 – а – 2 к рабочему телу подводится теплота q₁ , рабочее тело расширяется и производит работу, равную площади 1 – а – 2 – 3 – 4 – 1.

На участке 2 – б – 1 от рабочего тела отводится теплота q₂ (или выпускаются отработанные газы), а также рабочее тело сжимается, на что затрачивается отрицательная работа внешних сил соответствующая площади 2 – б – 1 – 4 – 3 – 2. В т. 1 цикл завершается и рабочее тело приобретает первоначальные параметры. Следовательно, внутренняя энергия рабочего тела не изменятся ( ).

На основании 1 – го закона термодинамики для цикла имеем:

(1.26)

А_ц – произведенная полезная работа.

Рассмотренный цикл называется прямым. По прямым циклам работают все тепловые двигатели.

Для непрерывной работы двигателя, превращающего теплоту в механическую энергию, необходимо иметь источник теплоты с высокой температурой Т₁ и сток теплоты (холодильник) с низкой температурой Т₂. При этом всегда желательно, чтобы в работу превратилась как можно большая доля подведенной теплоты.

Термический КПД цикла:

(1.27)

Термический КПД цикла – это отношение количества теплоты, превращенной в полезную работу, к количеству подведенной теплоты.

Рассмотрим цикл, осуществляющийся в обратном направлении, т.е. против часовой стрелки. Здесь линия сжатия расположена выше линии расширения, т.е. работа осуществляется на сжатие. Такой цикл называется обратным.

Положительная работа 1 – а – 2 – 3 – 4 меньше отрицательной 2 – б – 1 – 4 – 3, поэтому полезная работа не производится, а затрачивается работа от внешнего источника энергии. Теплота q₂ передается рабочему телу от холодного источника, а теплота q₁ отдается горячему источнику. В обратном цикле передача тепловой энергии происходит от холодного тела к горячему, при этом затрачивается работа, которая превращается в тепловую энергию.

(1.28)

Обратные циклы осуществляются в холодильных установках и тепловых насосах. Эффективность их работы оценивается холодильным коэффициентом:

(1.29)

Холодильный коэффициент – это отношение количества теплоты (тепловой энергии), переданное от холодного тела к количеству тепловой энергии, эквивалентной затраченной работе цикла А_ц .

В результате анализа множества циклов французский ученый Сади Карно нашел цикл с максимальным значением КПД.

Рис. 1.8. Перемещение поршня и изменение параметров рабочего тела в цикле Карно.

т. 1 – начало цикла: р₁, V₁, T₁

1-2 – изотермическое расширение рабочего тела при температуре Т₁ с подводом тепловой энергии q₁ и работой изотермического расширения 1 – 2 – 6 – 8 – 1.

2-3 – подвода теплоты нет, расширение по адиабате 2-3 до крайнего правого положения поршня 3. Работа адиабатного расширения 2 – 3 – 5 – 6 – 2.

3-4 – процесс сжатия рабочего тела при температуре Т₂ – изотермический процесс – с отводом теплоты q₂ и работой 3 – 4 – 7 – 5 – 3.

4-1 – процесс сжатия без отвода теплоты по адиабате 4-1, работа сжатия 4 – 1 – 8 – 7 – 4.

Таким образом, полезная работа определяется площадью 1 – 2 – 3 – 4 – 1 как разность площадей 1 – 2 – 3 – 5 – 8 – 1 и 3 – 4 – 1 – 8 – 5 – 3.

Термический КПД цикла Карно определяется по выражению:

(1.30)

В цикле Карно принято равенство отношений удельных объемов

(1.31)

С учетом последнего выражения

(1.32)

Из формулы (1.32) следует:

1. Термический КПД цикла Карно не зависит от свойств рабочего тела, а определяется только значением температур Т₁ и Т₂.

2. Термический КПД возрастает с увеличением Т₁ и уменьшением Т₂.

3. Термический КПД цикла Карно меньше единицы и может достигать 0,7 – 0,8.

Единице термический КПД цикла Карно мог бы быть равен при Т₂=0 или Т₁=∞,

что неосуществимо.

Реально создать двигатель, работающий по циклу Карно невозможно , т.к. процессы изотермического подвода и отвода тепловой энергии, а также адиабатного расширения и сжатия практически неосуществимы.

Цикл Карно является эталоном с максимальным КПД превращения тепловой энергии в работу. Реальный тепловой двигатель тем совершеннее, чем ближе его КПД к КПД цикла Карно, протекающего при тех же температурах.

Обратный цикл Карно также является эталоном для работы холодильных установок.

Холодильный коэффициент цикла Карно:

(1.33)

Второй закон термодинамики

(три его трактовки)

1. Для превращения тепловой энергии в механическую работу необходимо иметь источник тепловой энергии и холодильник с температурой ниже температуры источника.

2. При преобразовании тепловой энергии в работу часть тепловой энергии передается другим телам.

3. Тепловая энергия не может сама собой переходить от менее нагретого тела к более нагретому без затраты внешней работы.

Для превращения тепловой энергии в механическую работу необходимо иметь

источник тепловой энергии, причем только часть энергии источника перейдет в работу, а другая часть тепловой энергии должна перейти в теплоприемник.

Эта трактовка включает все три пункта.

1.6. Энтропия газа.

Рассмотрим произвольный обратимый процесс.

Рис. 1.9. Произвольный обратимый процесс в PV – диаграмме.

Для малого отрезка процесса подвод теплоты мал и равен dq и температура процесса для этого отрезка постоянна .

- называется приведенной теплотой.

Изменение приведенной теплоты в процессе 1 – 2

(1.34)

т.к.

то (1.35)

или (1.36)

После интегрирования имеем:

(1.37)

Величина S называется энтропией.

После подстановки уравнений состояний газа 1 и 2

(1.38)

Энтропия характеризует изменение состояния газа и направление тепловых потоков.

Знаки приращения энтропии dS и теплоты dq совпадают. Если энтропия возрастает, то тепловая энергия к газу подводится, если энтропия уменьшается, то тепловая энергия отводится от газа.

Рассмотрим основные термодинамичекие процессы в T – S диаграмме.

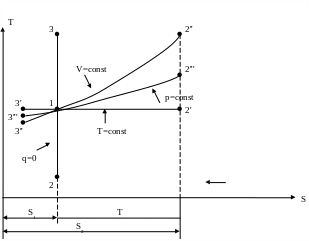
Рис. 1.10. Термодинамические процессы в TS – диаграмме.

1. И зохорный процесс

, кривая 3'' - 2''

Выражение (1.37) имеет вид (1.39)

1-2'' – нагрев газа, dT>0, dS>0

1-3'' – охлаждение газа, отвод теплоты dT<0, dS<0

2. Изобарный процесс

, кривая 3''' - 2'''

Выражение (1.37) принимает вид (1.40) (1.40)

3. Изотермический процесс

, кривая 3' - 2'

Выражение (1.37) принимает вид

(1.41)

1-2' – расширение газа dV>0, dS>0

1-3' – изотермическое сжатие газа

(1.42)

4. Адиабатный процесс

q=0, кривая 2-3

, (1.43)

1-2 – процесс расширения dT<0

1-3 – процесс сжатия

В T-S диаграмме цикл Карно соответствует прямоугольнику, ограниченному двумя изотермами и двумя адиабатами.