
- •1 Вариант
- •6. Показатели разработки нефтяного месторождения при упругом режиме (обводненность, нефтеотдача, дебит нефти и дебит воды).
- •7. Уравнение акустики. Постановка прямой задачи сейсморазведки для него.
- •8. Понятие об обратной задачи электроразведки.
- •9. Вывод нестационарного уравнения нестационарного распределения температуры в грунте.
- •2 Вариант
- •6.Конечно-разностная аппроксимация первой производной и ее погрешность.
- •7. Расчет падения давления на контуре нефтяной залежи при упругом режиме (прямоугольная область). Модель Карслоу-Егеря
- •Решение задачи 1.
- •9. Расчет кажущегося сопротивления при помощи трансформант..
- •3 Вариант
- •6. Блок-схема для расчета значений сплайна первого порядка.
- •7. Вывод уравнения Баклея-Леверетта для текущей обводненности.
- •8. Установка Шлюмберже. Нахождение кажущихся удельных электрических сопротивлений.
- •Вертикальное электрическое зондирование. Установка Шлюмберже.
- •9. Граничные и начальные условия для нестационарного уравнения распределения температуры в грунте.
- •4 Вариант
- •5 Вариант
- •Случай точечного источника
- •7. Схема решении обратной задачи электроразведки градиентным методом.
- •8. Последовательность вычислений решения задачи распростнения тепла от поверхности трубы до поверхности грунта. Постановка задачи
- •7.2. Математическая модель.
- •9. Стандартный метод Рунге-Кутта и его погрешность.
- •2. Метод Рунге – Кутта второго порядка точности.
- •3. Метод Рунге – Кутта третьего порядка точности.
- •4. Метод Рунге – Кутта четвертого порядка точности.
- •6 Вариант
- •6. Расчетные формулы сплайна первого порядка
- •8. Значения трансформанты сопротивления рассчитываются по соотношениям Пекериса.
- •Блок-схема основной программы
- •9. Стандартный метод Рунге-Кутта и его погрешность.
- •3. Метод Рунге – Кутта третьего порядка точности.
- •4. Метод Рунге – Кутта четвертого порядка точности.
- •7 Вариант
- •6. Метод прямоугольников для численного интегрирования. Погрешность.
- •8. Установка Шлюмберже. Схема измерений с помощью установки Шлюмберже..
- •Для установки Шлюмберже и , следовательно, (1.1) и (1.2) записываются следующим образом:
- •9. Схема численного решения прямой задачи сейсморазведки.
6 Вариант
6. Расчетные формулы сплайна первого порядка
X = a+ i*h
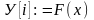
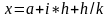
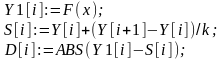
Ma : = Ma + D [i] /n
Sig : = Sig + SQR (D [i] – Ma) / (n-1) ;
Sig : = SQRT (Sig);
7. Постановка задачи нахождения стационарного распределения температуры в трубопроводе нефтеперевозки.
Длинный трубопровод с теплопроводностью λ (ккал/м.час град.) находится в состоянии теплового равновесия, т.е. температура точек трубопровода не изменяется во времени. Потеря тепла через поверхность трубопровода в окружающую среду, температура которой θ0 = const, пропорциональна разности температур с постоянным коэффициентом теплопередачи α (ккал/м2. час град.). Считая температуру θ во всех точах поперечного сечения трубопровода постоянной, найти ее зависимость θ = θ(х) от координаты, отсчитываемой от какого-либо конца.
8. Значения трансформанты сопротивления рассчитываются по соотношениям Пекериса.
Константы и переменные: nt=17; n=18; {число отсчетов}
R[1..10]; {удельные сопротивления}
T[1..nt]; {трансформанты сопротивления}
HS[1..9]; {мощности слоев}
x1, y, S, f, B: real; {х1- абсцисса первой точки измерения, у- текущая абсцисса, S – значение кажущегося сопротивления, f – шаг, B – текущие значения трансформанты сопротивления }
i9, i8, i, j, m : integer; {i9- число слоев, i8=i9-1, i, j, m- счетчики}
Procedure TI (var B: real); {вычисляет текущие значения трансформанты сопротивления}
begin
B:=R[i9]
нет
да
end
a1:=exp(u);
a2:=(a1-1/a1)/(a1+1/a1); B:=(B+a2*R[i])/(1+a2*B/R[i])
i:=i9-k;
u:=HS[i]/y

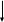









k:=1,i8
If
u<5
B:=R[i]

Блок-схема основной программы
begin
TI(B);
T[nt]:=B; y:=y*f;
j:=1,
nt-1
end
m:=1,n
j:=1,
nt-1
TI(B);
T[j]:=B; y:=y*f;
F:=exp(ln(10)/6);
y=x1*0,0105; B:=0
Ввод:
i9,
R[i], HS[i], x1













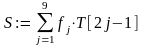 ;
вывод
(S)
;
вывод
(S)
T[j]:=T[j+1]
9. Стандартный метод Рунге-Кутта и его погрешность.
Метод Рунге – Кутта второго порядка точности.
Предположим, что приближенное значение решение исходной задачи в точке уже известно. Для нахождения поступим следующим образом. Сначала, используя схему Эйлера вычислим промежуточное значение , а затем воспользуемся разностным уравнением , из которого явным образом найдем искомое значение .
Погрешность метода. , где – константа, зависящая от исходных данных (3.1). Этот метод имеет второй порядок точности.
3. Метод Рунге – Кутта третьего порядка точности.
Считаем, что решение задачи (3.1) – (3.2) в точке уже известно. Тогда решение задачи (3.1) – (3.2) определяется по следующей схеме:
Погрешность метода.
, где – константа, не зависящая от к.
4. Метод Рунге – Кутта четвертого порядка точности.
Погрешность метода.
, где – константа, зависящая от начальных данных и не зависящая от к.
Замечание: Метод Рунге-Кутта также применяется, если неизвестная функция является вектором, т.е.
, где
