- •1 Вариант
- •6. Показатели разработки нефтяного месторождения при упругом режиме (обводненность, нефтеотдача, дебит нефти и дебит воды).
- •7. Уравнение акустики. Постановка прямой задачи сейсморазведки для него.
- •8. Понятие об обратной задачи электроразведки.
- •9. Вывод нестационарного уравнения нестационарного распределения температуры в грунте.
- •2 Вариант
- •6.Конечно-разностная аппроксимация первой производной и ее погрешность.
- •7. Расчет падения давления на контуре нефтяной залежи при упругом режиме (прямоугольная область). Модель Карслоу-Егеря
- •Решение задачи 1.
- •9. Расчет кажущегося сопротивления при помощи трансформант..
- •3 Вариант
- •6. Блок-схема для расчета значений сплайна первого порядка.
- •7. Вывод уравнения Баклея-Леверетта для текущей обводненности.
- •8. Установка Шлюмберже. Нахождение кажущихся удельных электрических сопротивлений.
- •Вертикальное электрическое зондирование. Установка Шлюмберже.
- •9. Граничные и начальные условия для нестационарного уравнения распределения температуры в грунте.
- •4 Вариант
- •5 Вариант
- •Случай точечного источника
- •7. Схема решении обратной задачи электроразведки градиентным методом.
- •8. Последовательность вычислений решения задачи распростнения тепла от поверхности трубы до поверхности грунта. Постановка задачи
- •7.2. Математическая модель.
- •9. Стандартный метод Рунге-Кутта и его погрешность.
- •2. Метод Рунге – Кутта второго порядка точности.
- •3. Метод Рунге – Кутта третьего порядка точности.
- •4. Метод Рунге – Кутта четвертого порядка точности.
- •6 Вариант
- •6. Расчетные формулы сплайна первого порядка
- •8. Значения трансформанты сопротивления рассчитываются по соотношениям Пекериса.
- •Блок-схема основной программы
- •9. Стандартный метод Рунге-Кутта и его погрешность.
- •3. Метод Рунге – Кутта третьего порядка точности.
- •4. Метод Рунге – Кутта четвертого порядка точности.
- •7 Вариант
- •6. Метод прямоугольников для численного интегрирования. Погрешность.
- •8. Установка Шлюмберже. Схема измерений с помощью установки Шлюмберже..
- •Для установки Шлюмберже и , следовательно, (1.1) и (1.2) записываются следующим образом:
- •9. Схема численного решения прямой задачи сейсморазведки.
7.2. Математическая модель.
Ось ОХ направим вертикально вверх (рис. 1). На оси ОХ выделим элемент с координатами х и х + Δх. Тогда приращение энергии в направлений оси х за время Δt будет
(7.1)
С другой стороны, согласно закону сохранения энергий,
(7.2)
Левые части (7.1) и (7.2) равны, поэтому
где ρ– плотность грунта [кг/м3];
с – массовая теплоемкость грунта [кдж/кг.град];
λ – коэффициент теплопроводности грунта [вт/м·град.].
При х = 0 задается температура . На поверхности земли происходит конвективный теплообмен между поверхностью тела и окружающей средой (воздух).
В основу изучения конвективного теплообмена положен закон Ньютона-Рихмана
где q – плотность теплового потока, вт/м2;
θ0 – температура воздуха, 0С;
θгр – температура поверхности грунта,0С;
α – коэффициент теплоотдачи, вт/(м2·град);
Согласно закону сохранения энергии, количество теплоты, отдаваемый единицей поверхности тела окружающей среде за единицу времени вследствие теплоотдачи, должно быть равно теплоте, которая путем теплопроводности подводится к единице поверхности в единицу времени со стороны внутренних частей тела, т.е.
(7.3)
Равенство (7.3) является математической формулировкой граничного условия третьего рода; оно является действительной для каждого момента времени t.
называется граничным условием первого рода.
Получена задача: найти решение нестационарного параболического уравнения со смешанными граничными условиями, т.е.
(7.4)
θ(t,0) = θ1 = const (7.5)
(7.6)
(7.7)
Теорема 1. При определенных условиях на ρ(θ), с(θ) и λ(θ) задача (7.4) - (7.7) имеет единственное решение.
9. Стандартный метод Рунге-Кутта и его погрешность.
2. Метод Рунге – Кутта второго порядка точности.
Предположим,
что приближенное значение
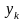 решение исходной задачи в точке
решение исходной задачи в точке
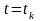 уже известно. Для нахождения
уже известно. Для нахождения
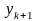 поступим следующим образом. Сначала,
используя схему Эйлера
поступим следующим образом. Сначала,
используя схему Эйлера 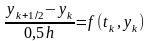 вычислим промежуточное значение
вычислим промежуточное значение
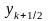 ,
а затем воспользуемся разностным
уравнением
,
а затем воспользуемся разностным
уравнением 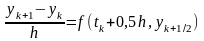 ,
из которого явным образом найдем искомое
значение
.
,
из которого явным образом найдем искомое
значение
.
Погрешность
метода.
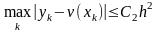 ,
где
,
где
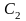 – константа, зависящая от исходных
данных (3.1). Этот метод имеет второй
порядок точности.
– константа, зависящая от исходных
данных (3.1). Этот метод имеет второй
порядок точности.
3. Метод Рунге – Кутта третьего порядка точности.
Считаем,
что решение задачи (3.1) – (3.2) в точке
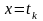 уже известно. Тогда решение задачи (3.1)
– (3.2) определяется по следующей схеме:
уже известно. Тогда решение задачи (3.1)
– (3.2) определяется по следующей схеме:
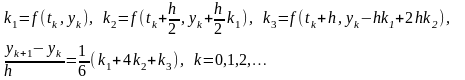
Погрешность метода.
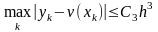 ,
где
,
где
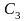 – константа, не зависящая от к.
– константа, не зависящая от к.
4. Метод Рунге – Кутта четвертого порядка точности.
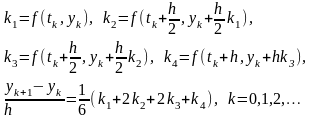
Погрешность метода.
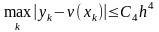 ,
где
,
где
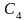 – константа, зависящая от начальных
данных и не зависящая от к.
– константа, зависящая от начальных
данных и не зависящая от к.
Замечание: Метод Рунге-Кутта также применяется, если неизвестная функция является вектором, т.е.
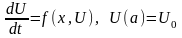 ,
где
,
где