9. Расчет кажущегося сопротивления при помощи трансформант..

Согласно О.Куфуду введем трансформанту сопротивления.

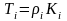(2.9)

Выразив рекурентные соотношения Пекериса через трансформанту сопротивления, получим

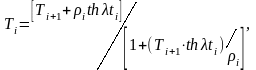(2.10)

и в обращенной форме

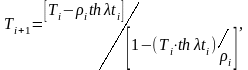(2.11)

Трансформанта сопротивления имеет физическую размерность удельного сопротивления. Эта функция параметров слоев и параметра 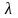, который имеет размерность обратного расстояния. Теперь можно определить соотношение между кажущимся сопротивлениям 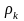и трансформантой сопротивления для установки Шлюмберже. Для этого в формулу

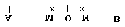где 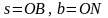- полуразносы питающих и измерительных электродов (рис.6), надо вместо 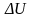подставить выражение из (2.4). Тогда получим Рис.6.

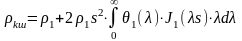(2.12)

где

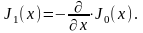
Это уравнения согласно (2.5), (2.8) удобно записать в виде

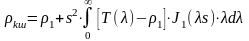(2.13)

По последнему уравнению можно теоретически определять , т.е. решать прямую задачу ВЭЗ.

3 Вариант

6. Блок-схема для расчета значений сплайна первого порядка.

начало

а, в, n, k, f(x),b[0]

I : = Ø, n, 1

У[i] = f(x)

I : = Ø, n-1, 1

У1[i] = f(x)

I : = Ø, n-1, 1

I : = Ø, n-1, 1

S[i]: = У[i]+(У[i+1]- У[i]) / k

I : = Ø, n-1, 1

Del[i]:=ABS(Y1[i]-S[i])

I : = Ø, n-1, 1

Ma : = Ma + D [i] / n

Y1[I],Y[i],S[i],Del[i],Ma,sig

конец

Sig:=sig+sqrt(Del[i]-Ma)/(n-1)

Sig:=sqrt(sig)

7. Вывод уравнения Баклея-Леверетта для текущей обводненности.

Текущая обводненность продукции скважин определяется следующим соотношением: дебит воды, добываемой одновременно с нефтью из всех скважин;

q_н – дебит нефти.

Понятно, что . Так как кривая на рис.3.1 выражает зависимость .

Поскольку получим . Из предыдущего равенства имеем

. или . (3.1)

. (3.2)

Полученная задача Коши (3.1) – (3.2) решается различными численными методами.

Теория вытеснения нефти водой, развитая Баклеем и Левереттом, изложена в [4]. В качестве аппроксимирующей функций зависимости приведенной в рис.6 используем выражение

(3.3)

3. называется функцией Баклея – Леверетта, где а – положительная константа.

8. Установка Шлюмберже. Нахождение кажущихся удельных электрических сопротивлений.