
- •1 Вариант
- •6. Показатели разработки нефтяного месторождения при упругом режиме (обводненность, нефтеотдача, дебит нефти и дебит воды).
- •7. Уравнение акустики. Постановка прямой задачи сейсморазведки для него.
- •8. Понятие об обратной задачи электроразведки.
- •9. Вывод нестационарного уравнения нестационарного распределения температуры в грунте.
- •2 Вариант
- •6.Конечно-разностная аппроксимация первой производной и ее погрешность.
- •7. Расчет падения давления на контуре нефтяной залежи при упругом режиме (прямоугольная область). Модель Карслоу-Егеря
- •Решение задачи 1.
- •9. Расчет кажущегося сопротивления при помощи трансформант..
- •3 Вариант
- •6. Блок-схема для расчета значений сплайна первого порядка.
- •7. Вывод уравнения Баклея-Леверетта для текущей обводненности.
- •8. Установка Шлюмберже. Нахождение кажущихся удельных электрических сопротивлений.
- •Вертикальное электрическое зондирование. Установка Шлюмберже.
- •9. Граничные и начальные условия для нестационарного уравнения распределения температуры в грунте.
- •4 Вариант
- •5 Вариант
- •Случай точечного источника
- •7. Схема решении обратной задачи электроразведки градиентным методом.
- •8. Последовательность вычислений решения задачи распростнения тепла от поверхности трубы до поверхности грунта. Постановка задачи
- •7.2. Математическая модель.
- •9. Стандартный метод Рунге-Кутта и его погрешность.
- •2. Метод Рунге – Кутта второго порядка точности.
- •3. Метод Рунге – Кутта третьего порядка точности.
- •4. Метод Рунге – Кутта четвертого порядка точности.
- •6 Вариант
- •6. Расчетные формулы сплайна первого порядка
- •8. Значения трансформанты сопротивления рассчитываются по соотношениям Пекериса.
- •Блок-схема основной программы
- •9. Стандартный метод Рунге-Кутта и его погрешность.
- •3. Метод Рунге – Кутта третьего порядка точности.
- •4. Метод Рунге – Кутта четвертого порядка точности.
- •7 Вариант
- •6. Метод прямоугольников для численного интегрирования. Погрешность.
- •8. Установка Шлюмберже. Схема измерений с помощью установки Шлюмберже..
- •Для установки Шлюмберже и , следовательно, (1.1) и (1.2) записываются следующим образом:
- •9. Схема численного решения прямой задачи сейсморазведки.
1 Вариант
6. Показатели разработки нефтяного месторождения при упругом режиме (обводненность, нефтеотдача, дебит нефти и дебит воды).
Задача
3. Для условий, данных в задаче 2 требуется
определить изменение добычи нефти,
воды, текущей нефтеотдачи и обводненности
продукции при заданной динамике жидкости
в течение 15 лет. Для рассматриваемого
месторождения известны данные зависимости
(рис.3.1) текущей обводненности продукции
от отношения
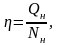 (Qн – накопленная добыча нефти, Nн –
запасы нефти). Считается, что эта
зависимость будет справедливой в течение
(Qн – накопленная добыча нефти, Nн –
запасы нефти). Считается, что эта
зависимость будет справедливой в течение
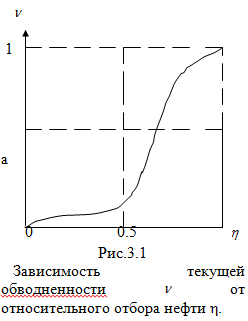
Текущая обводненность продукции скважин определяется следующим соотношением:
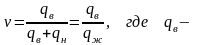 дебит
воды, добываемой одновременно с нефтью
из всех скважин;
дебит
воды, добываемой одновременно с нефтью
из всех скважин;
qн – дебит нефти.
Понятно,
что
 . Так как кривая на рис.3.1 выражает
зависимость
. Так как кривая на рис.3.1 выражает
зависимость
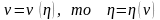 .
.
Поскольку
 получим
получим
 . Из предыдущего равенства имеем
. Из предыдущего равенства имеем
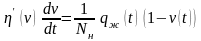 .
или
.
или
 .
(3.1)
.
(3.1)
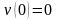 (3.2)
(3.2)
Полученная задача Коши (3.1) – (3.2) решается различными численными методами.
Теория вытеснения нефти водой, развитая Баклеем и Левереттом, изложена в [4]. В качестве аппроксимирующей функций зависимости приведенной в рис.6 используем выражение
 (3.3)
(3.3)
(3.3) называется функцией Баклея – Леверетта, где а – положительная константа.
7. Уравнение акустики. Постановка прямой задачи сейсморазведки для него.
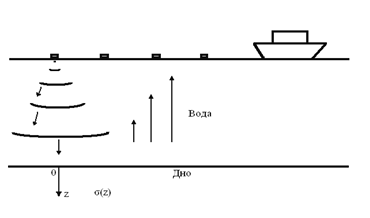

Задача (1) – прямая задача акустики: по падающей волне g(t) и известной акустической жесткости среды σ(z) требуется определить реакцию среды (z > 0)
u(0,t)=f(t) – сейсмограмму.
Обратная задача (1), (2): по заданным g(t) и f(t) требуестя определить строение морского дна, т.е. акустическую жесткость среды σ(z).
Конечно-разностный метод решения прямой задачи
Решаем
прямую задачу конечно-разностным
методом. Пусть
 , где l – глубина, N – число разбиений.
Заменим производные конечно-разностными
аналогами:
, где l – глубина, N – число разбиений.
Заменим производные конечно-разностными
аналогами:

Схему (11) упростим, сокращая и группируя подобные слагаемые:
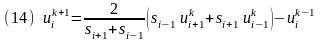
.
Из (13) находим
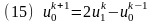 .
.
Алгоритм решения прямой задачи:
1) Находим
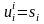 , при
, при
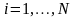 ;
;
2) По
формуле (15) определяем
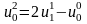 ;
;
3) Из
схемы (14) находим
 ;
;
4) Из
(15) находим
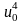 ;
;
5) По
формуле (14) определяем
 ;
;
6) По
формуле (14) определяем
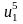 ;
;
7) Из
(15) находим
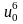 ;
;
и т.д.
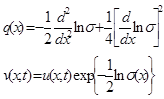
8. Понятие об обратной задачи электроразведки.
Решение обратной задачи электроразведки градиентным методом.
Для разработки прикладной программы на языке Турбо-Паскаль 7.0 и решения обратной задачи, будем использовать следующую версию градиентного метода. Функционал невязки вычисляется как среднее квадратов относительных разностей между дискретными значениями кажущегося сопротивления, полученными по полевым данным и для теоретической модели. Таким образом
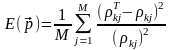 (4.4)
(4.4)
 (4.5)
(4.5)
В
качестве градиента невязки Е берется
вектор с компонентами
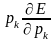 .
.
9. Вывод нестационарного уравнения нестационарного распределения температуры в грунте.
7.1. Постановка задачи
Подогретый до температуры θ1 (град.) нефть перевозится по подземному трубопроводу.
Глубина прокладки нефтепровода Н(м).
Считая, что теплоотдача происходит только по вертикальному направлению определить распределение температуры от трубы до поверхности земли.
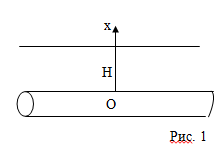
Ось ОХ направим вертикально вверх (рис. 1). На оси ОХ выделим элемент с координатами х и х + Δх. Тогда приращение энергии в направлений оси х за время Δt будет
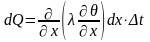 (7.1)
(7.1)
С другой стороны, согласно закону сохранения энергий,
 (7.2)
(7.2)
Левые части (7.1) и (7.2) равны, поэтому
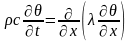
где ρ– плотность грунта [кг/м3];
с – массовая теплоемкость грунта [кдж/кг.град];
λ – коэффициент теплопроводности грунта [вт/м•град.].
При х = 0 задается температура . На поверхности земли происходит конвективный теплообмен между поверхностью тела и окружающей средой (воздух).
В основу изучения конвективного теплообмена положен закон Ньютона-Рихмана
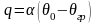
где q – плотность теплового потока, вт/м2;
θ0 – температура воздуха, 0С;
θгр – температура поверхности грунта,0С;
α – коэффициент теплоотдачи, вт/(м2•град);
Согласно закону сохранения энергии, количество теплоты, отдаваемый единицей поверхности тела окружающей среде за единицу времени вследствие теплоотдачи, должно быть равно теплоте, которая путем теплопроводности подводится к единице поверхности в единицу времени со стороны внутренних частей тела, т.е.
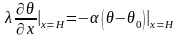 (7.3)
(7.3)
Равенство (7.3) является математической формулировкой граничного условия третьего рода; оно является действительной для каждого момента времени t.
называется граничным условием первого рода.
Получена
задача: найти решение нестационарного
параболического уравнения со смешанными
граничными условиями, т.е.
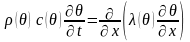 (7.4)
(7.4)
θ(t,0) = θ1 = const (7.5)
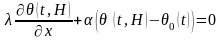 (7.6)
(7.6)
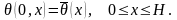 (7.7)
(7.7)
Теорема 1. При определенных условиях на ρ(θ), с(θ) и λ(θ) задача (7.4) - (7.7) имеет единственное решение.
Приближенный метод решения задачи (7.4) – (7.6).
Решение
задачи (7.4) – (7.6) зависит от двух переменных
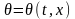 , где t – время, час; х – координата точки
грунта, м. Поэтому задача (7.4) – (7.6)
решается в области Q= (0, Тmax)•(0,H),
, где t – время, час; х – координата точки
грунта, м. Поэтому задача (7.4) – (7.6)
решается в области Q= (0, Тmax)•(0,H),

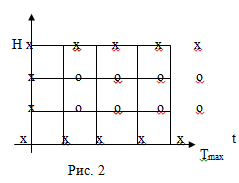
Сетка.
Отрезок [0, H] разбиваем на N равных частей
с шагом h = H/N, а отрезок [0, Tmax] на М равных
частей с шагом ∆t = Tmax /M. Тогда получается
сетка (рис. 2).

В рис.2 «крестиками» - х обозначены граничные узлы, а «ноликами» - 0 обозначены внутренние узлы.
Аппроксимация выражений
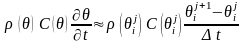
т.е. функций ρ(θ) и с(θ) определяются на нижних слоях. В начальный момент времени, т.е. при
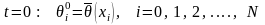 .
.
Вместо задачи (7.4) – (7.7) решается приближенная задача
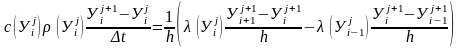 (7.8)
(7.8)
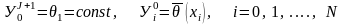 (7.9)
(7.9)
 (7.10)
(7.10)
В системе (7.8) i = 1, 2, …, N-1 при каждом j=0,1,…,M-1.
Систему линейных алгебраических уравнений перепишем в виде
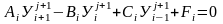 (7.11)
(7.11)
i = 1, 2, …, N-1 при каждом j=0,1,…,M-1.
Где

