Задача 3

Вы имеете 10 млн. грн. и хотели бы удвоить эту сумму через 5 лет. Каково минимально приемлемое значение процентной ставки?

Стратегия решения

Известно, что PV = 10 млн. грн. Схема начисления процентов не указана, следовательно – сложная. Периоды начисления не оговариваются, следовательно, период начисления – ежегодно. Тогда n = 5, FV = 20 млн. грн. Найти величину i.

Решение задачи

Используем формулу (6) в которой неизвестной величиной есть i.

Из этой формулы выразим i, получим:

Ответ: Для того чтобы удвоить 10 млн. грн. через 5 лет необходимо их положить на депозитный счет под минимально приемлемую ставку, равную 14,9%.

4. Приведенная стоимость

В финансах часто используется понятие ПРИВЕДЕННАЯ СТОИМОСТЬ. Суть этого понятия раскроем на примере решения задачи 4.

Задача 4

Какая сумма денег для Вас предпочтительнее при годовой процентной ставке 9%: $1000 сегодня или $2000 через 8 лет?

Стратегия решения

Решение задачи предполагает выбор Вами одной из денежных сумм – $1000 сегодня или $2000 через 8 лет. Проблема выбора одной из вышеуказанных сумм состоит в том, что эти суммы находятся в разном времени. $1000 Вы можете «взять» сейчас, сегодня, а чтобы «взять» $2000 Вам надо ждать 8 лет, после чего Вы их можете “получить”. Естественно, Вы будете выбирать большую сумму денег. Поэтому нужно узнать какая из сумм денег больше – $1000 сегодня или $2000 через 8 лет.

В связи с тем, что СТОИМОСТЬ ДЕНЕГ ИЗМЕНЯЕТСЯ ВО ВРЕМЕНИ, сравнивать $1000 сегодня и $2000 через 8 лет можно только при условии, что сравниваемые суммы находятся в одном и том же времени.

Условие задачи можно изобразить графически (рис. 1):

9 % 9% 9% 9% 9% 9% 9% 9%

Г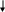 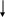оды: 0 1 2 3 4 5 6 7 8

Деньги: $1000 $2000

Рисунок 1.

На рисунке 1 изображена временная ось. Точка 0 обозначает начало первого года (это и ест наше «сегодня»), точка 1 – конец первого года и начало второго, точка 2 – конец 2-го года и начало 3-го, и т.д. Точка 8 – конец 8-го года (это и есть наше «будущее»). Из условия задачи – ставка процентная, начисление процентов – ежегодное.

Для выяснения вопроса, какая из сумм больше – $1000 сегодня или $2000 через 8 лет, механизм расчета следующий: $1000 сегодня мы пересчитываем в будущее время – на конец 8-го года и после этого пересчета будущую стоимость $1000 сравниваем с $2000, т.е. выясняем, какая из сумм больше.

Решение задачи

Находим стоимость $1000 через 8 лет. Другими словами, находим какой суммой станет $1000, если ее положить в банк на срок 8 лет под 9% годовых с ежегодным сложным начислением процентов. Используем формулу (6) .

FV₁₀₀₀ = $1000(1+0,09)⁸ = $1992,56

Расчет показывает, что будущая стоимость $1000 через 8 лет будет равна $1992,56. Величина $1992,56 может сравниваться, сопоставляться с величиной $2000, т.к. эти величины находятся в одном времени. Следовательно, $2000 через 8 лет предпочтительнее, чем $1000 сегодня, конечно, если условия задачи будут выполнены.

Эта задача может быть решена другим способом.

Находим стоимость $2000 сегодня. Другими словами, находим, какую сумму надо было бы иметь сегодня, чтобы положив ее в банк на 8 лет под 9% годовых с ежегодным сложным начислением процентов, получить через 8 лет $2000.

Для решения этого вопроса используем формулу (9):

Расчет показывает, что настоящая стоимость $2000 равна $1003,73. Величина $1003,73 может сравниваться, сопоставляться с величиной $1000, т. к. эти величины находятся в одном времени. Следовательно, $2000 через 8 лет предпочтительнее, чем $1000 сегодня, конечно, если условия задачи будут выполнены.

Ответ. $2000 через 8 лет предпочтительнее, чем $1000 сегодня.

При решении задачи 4 мы ПЕРЕВОДИЛИ (пересчитывали) стоимость $1000 сегодняшнюю в будущую стоимость, а при решении вторым способом будущую стоимость $2000 ПРИВОДИЛИ (пересчитывали) в стоимость настоящую, или, как ее называют финансисты, текущую. Таким образом, можно сделать вывод, что ПЕРЕВЕДЕНИЕ стоимости и ПРИВЕДЕНИЕ стоимости – это ПЕРЕСЧЁТ стоимости по формулам (5), (6), (7), (8), (9) в зависимости от условий пересчёта.

Пересчёт стоимости из настоящего момента времени к определенному моменту в будущем называется МУЛЬТИПЛИКАЦИЯ. Формулы (5), (6), соответствующие такому пересчёту, называются МУЛЬТИПЛИКАТИВНЫМИ. Пересчёт будущей стоимости к настоящему моменту времени называется ДИСКОНТИРОВАНИЕМ. Следовательно, дисконтный пересчёт предполагает использование формул (7), (8), (9).

Формула (9) имеет самостоятельное значение и трактуется в расчетах, как ФОРМУЛА ПРИВЕДЕНИЯ. Безразмерный коэффициент в этой формуле в виде - называется КОЭФФИЦИЕНТОМ ДИСКОНТИРОВАНИЯ или, как часто встречается в литературе, ДИСКОНТОМ.