1.2. Процентные ставки и методы их начисления.

Простые и сложные проценты.

Стандартным временным интервалом в финансовых операциях является один год. Поэтому наиболее распространен вариант, когда процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечение года.

Известны две основные схемы дисконтированного начисления процентов:

• Схема простых процентов (simple interest).

• Схема сложных процентов (compound interest).

Схема простых процентов предполагает неизменность базы, с которой происходит начисление.

. (4)

Схема сложных процентов предполагает, что очередной годовой доход исчесляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные, и невостребованные инвестором проценты.

. (5)

Очень важно помнить, что

- при 0 < n < 1

- при n = 1

- при n > 1

Таким образом, в случае ежегодного начисления процентов, для лица, предоставляющего кредит:

• выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);

• более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);

• обе схемы дают одинаковые результаты при продолжительности периода в один год и однократном начислении процентов (рис. 2).

Пример 1.

Рассчитать наращенную сумму с исходной суммы 1000$ при размещении ее в банке на условиях начисления простых и сложных процентов, если годовая ставка 20 %, период наращивания: 90 дн., 180 дн., 1 год, 5 лет, 10 лет.

($)

Рис. 2. Простая и сложная схема наращивания капитала.

Пример2.

Компания хочет купить машину для снятия фотокопий за 10 000$. Продавец согласен, чтобы компания выплатила деньги по истечение 2 лет, при условии, что она заплатит за это 14 простых процентов за каждый год. Определить сумму процентов и полную выплату.

Проценты:

,

.

Если продавец машины согласен на отсрочку платежа всего на 90 дней, тогда

.

Если продавец машины согласен на отсрочку платежа на 15 месяцев, тогда

.

Процедура начисления процентов на проценты (сложные проценты) называются компаундингом.

Множитель называется коэффициентом аккумулирования.

Пример 3.

Вклад 3000$ помещены в банк под 5 % годовых на 3 года. Какая сумма будет накоплена через 3 года (сложные %)?

.

Пример 4.

Предприниматель желает инвестировать значительную сумму денег в акции некоторой корпорации. Корпорация выплачивает ежегодно дивиденды на одну акцию в сумме 3 %. Ожидается, что в течение ближайших 3 лет дивиденды будут увеличиваться ежегодно на 20 %. Рассчитать величину дивидендов для каждого года.

,

,

.

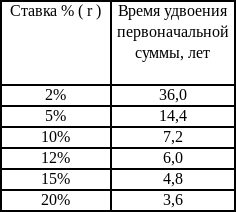
В практических расчетах при реализации схемы сложных процентов для быстрой оценки эффективности предлагаемой процентной ставки пользуются приблизительным расчетом времени, необходимого для удвоения инвестированной суммы. Это правило называется «правило 72-х» и заключается в следующем: если r-процентная ставка, выраженная в процентах, то k = 72/r представляет собой число периодов, за которое исходная сумма приблизительно удваивается. Если базовым периодом, т. е. периодом наращивания является год, то в расчете используется годовая ставка, если квартал, то необходимо использовать квартальную ставку.

Это правило хорошо срабатывает для небольших значений r (до 20 %).