3.Самостоятельное решение задач.

Пример №1 (263)

Дана функция распределения непрерывной случайной величины Х:

Найти плотность распределения f(x).

Пример №2 (338).

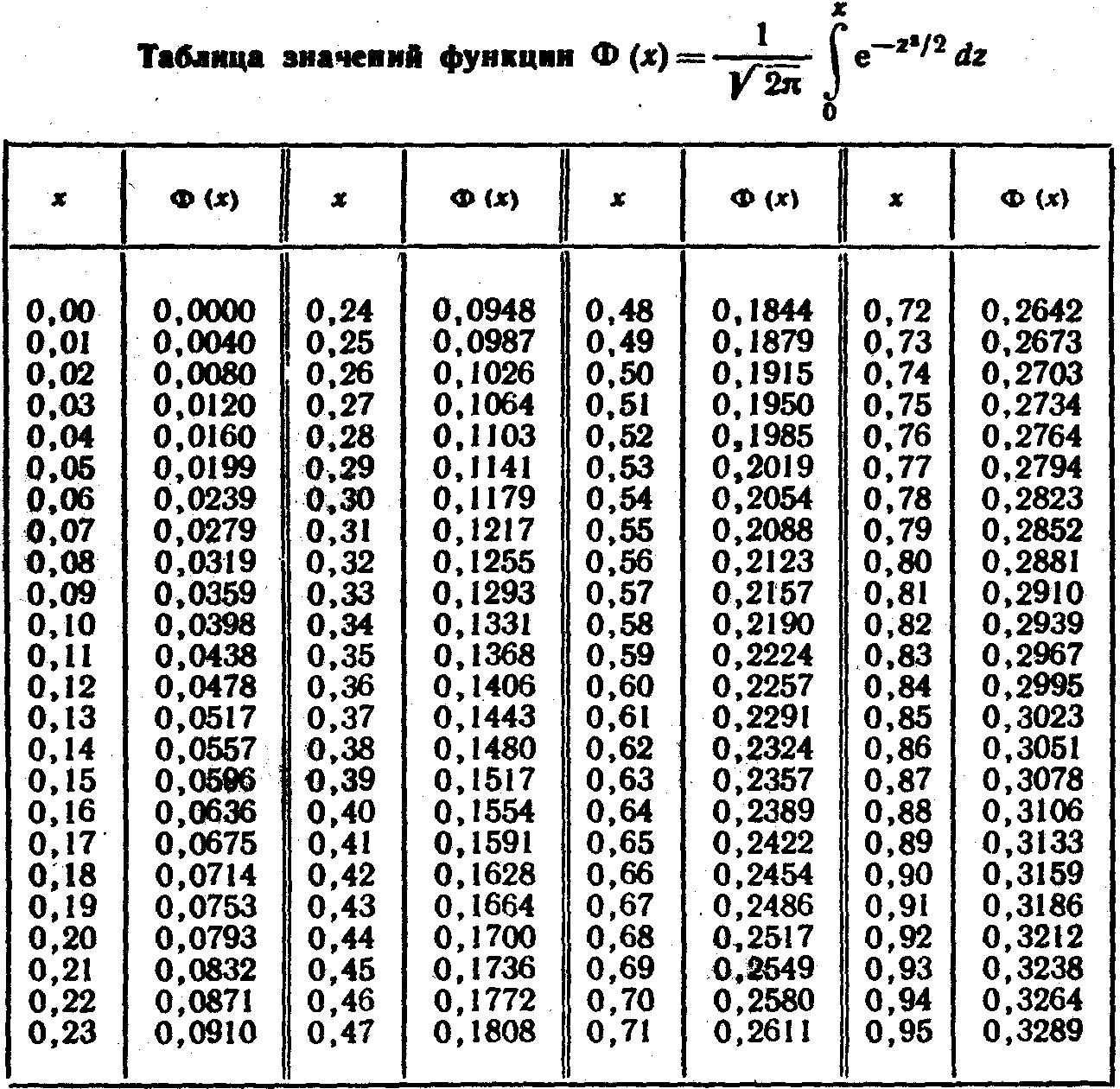
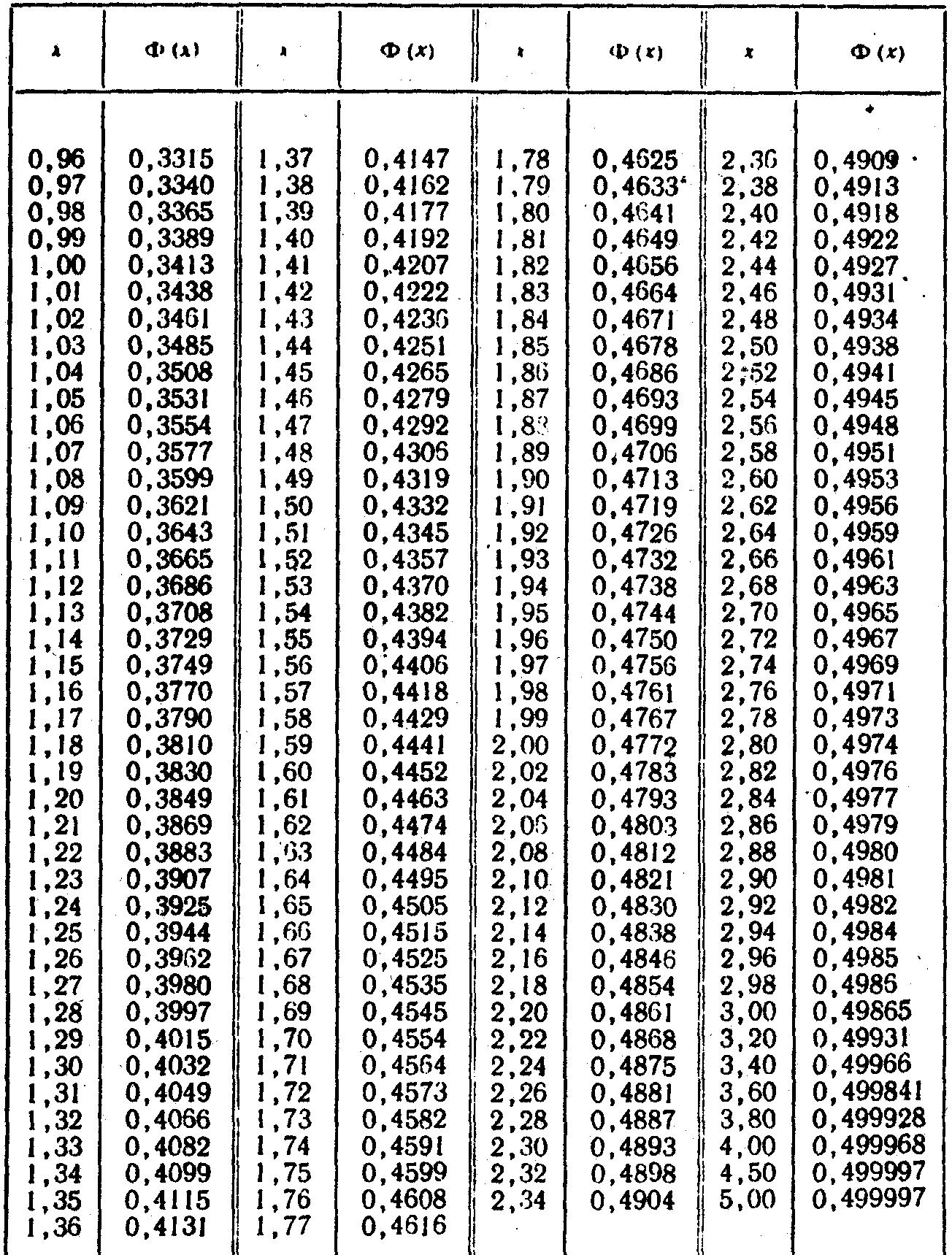
Случайная величина X распределена нормально с математическим ожиданием а = 25. Вероятность попадания Χ в интервал (10, 15) равна 0,2. Чему равна вероятность попадания Χ в интервал (35, 40)?

Пример №3 (268)

Задана плотность распределения непрерывной случайной величины Х:

Найти функцию распределения F(x).

Пример №4 (329)

Математическое ожидание и среднее квадратическое отклонение нормально распределённой случайной величины Х соотвтственно равны 20 и 5. Найти вероятность того, что в результате испытания Х примет значение, заключённое в интервале (15, 25).

Пример №5 (332)

Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону распределения с СКО равным 20 г. Найти вероятностьтого, что взвешивание будет произведено с ошибкой, не превышающей по абсолютной величине 10г.

Пример №6

Заработная плата сотрудников предприятия в течении последних 5ти лет изменяется случайным образом и может быть описана нормальным законом распределения с математическим ожиданием т_х = 10200 руб. и средним квадратичным отклонением = 2200 руб.

Найти вероятность того, что текущая зароботная плата будет находиться в пределах 5200 руб х < 16000 руб. С помощью правила трех сигм найти границы, в которых должна находиться текущая заработная плата и вероятность нахождения её в этих границах.