10

«Утверждаю»

Заведующий кафедрой

«Управление качеством и

техническое регулирование» ВлГУ ________Ю.А. Орлов

«__»_______2013 г.

Методическая разработка для проведения практического занятия

по дисциплине «Теория вероятностей, математическая статистика» для бакалавров направления 221400.62 «Управление качеством»

Тема №2. Случайные величины и их законы распределения

Занятие №2.9 Решение задач по определению плотности распределения и на нормальный закон распределения

Вид занятия: практическое (6)

Литература: 1. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб.пособие для вузов.-8-е изд.,стер.-М.:Высш.шк.,2002-479 с. (116-122). 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб.пособие для студентов вузов.Изд.5-е,стер.-М:.Высш.,шк.,2001.-400 с.(91,92,109-112).

Владимир 2013 план

проведения занятия

№ п/п	Учебные вопросы занятия	Время, мин.
I. II	Вводная часть: Объявление темы, темы занятия. Постановка учебных целей занятия. Основная часть.	2-3 75
	Решение задач по определению плотности распределения непрерывной случайной величины. Решение задач на нормальное распределение случайных величин. 3. Самостоятельное решение задач.
III.	Заключительная часть	2-3
	Подведение итогов занятия. Выдача задания на самостоятельную работу.

МАТЕРИАЛ ОСНОВНОЙ ЧАСТИ ЗАНЯТИЯ

1. Решение задач по определению плотности распределения непрерывной случайной величины

Плотностью распределения вероятностей непрерывной случай­ной величины называют первую производную от функции распределения:

Часто вместо термина «плотность распределения» используют термины «плотность Вероятностей» и «дифференциальная функция».

Вероятность того, что непрерывная случайная величина Χ примет значение, принадлежащее интервалу (а, b), определяется равенством:

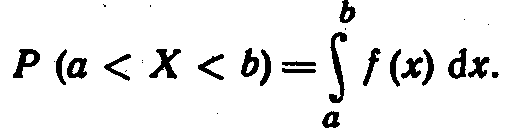
Зная плотность распределения, можно найти функцию распределения

Плотность распределения обладает следующими свойствами:

Свойство 1. Плотность распределения неотрицательна, т. е,

F(х)≥0.

Свойство 2. Несобственный интеграл от плотности распределения в пределах от до равен единице:

В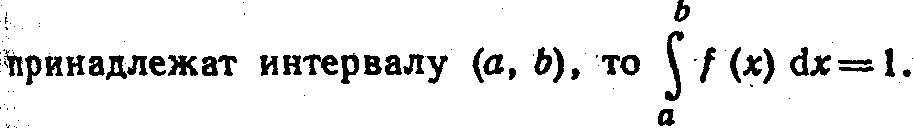 частности, если все возможные значения случайной величины принадлежит интервалу (a,b), то

Модой M₀ (x) непрерывной случайной величины X называют то ее возможное значение, которому соответствует локальный макси­мум плотности распределения. В частности, если распределение имеет два одинаковых максимума, то его называют бимодальным.

Медианой М_e(X) непрерывной случайной величины Χ называют то ее возможное значение, которое определяется равенством

Геометрически медиану можно истолковать как точку, в которой ордината f (х) делит пополам площадь, ограниченную кривой рас­пределения.

ПРИМЕР № 1 (262). Дана функция распределения непрерывной случайной величины Χ

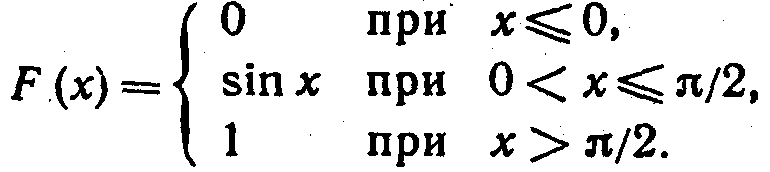
Найти плотность распределения f(x) и построить её график.

Решение. Плотность распределения равна первой производной от функции распределения:

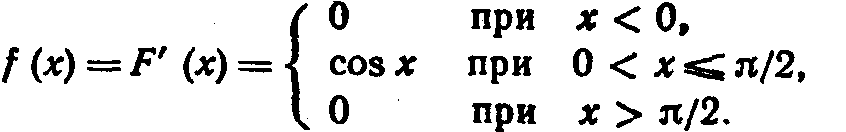
ПРИМЕР № 2 (267). Задана плотность распределения непрерывной случайной величины X:

Найти функцию распределения F(x) и построить её график.

Решение. Используем формулу

Итак, искомая функция распределения

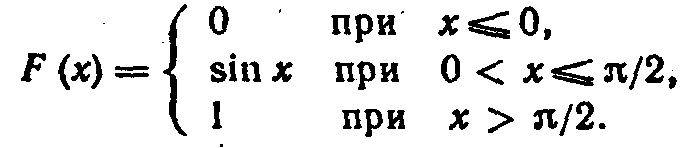
Построим график искомой функции:

Пример №3 (273). Плотность распределения непрерывной случайной величины Х в интервале (0, π/2) равна f(x)=C SIN(2X); вне этого интервала равна f(x)=0.

Найти постоянный параметр С.

Решение.

В соответствии с частным случаем свойства №2 плотности распределения

если x Є (а,в).

Тогда:

Далее используем табличное значение неопределённого интеграла:

.

Теперь, можно вычислить определённый интеграл:

Используя выражение (*), окончательно вычисляем значение «С»:

С = 1/1=1.