Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Санкт-Петербургский государственный университет технологии и дизайна»

Кафедра автоматизации производственных процессов

Моделирование случайного процесса изменения давления

Курсовая работа по дисциплине

«Моделирование систем»

Вариант 8

Выполнила студ. Гр.4-МД-5

Кислицина К.А.

Проверил проф. Смирнов И.Н.

Санкт-Петербург

2013

Содержание

1. Цель работы…………………………………………………….…3

2. Исходные данные о процессе…………………………………….3

3. Основной алгоритм……………….………………………………4

4. Выбор параметров процесса моделирования…………………...5

5. Обработка результатов моделирования…………………………6

6. Составление программы………………………………………….7

7. График……………………………………………………………..10

1. Цель работы

Целью работы является компьютерное моделирование стационарного случайного процесса изменения давления в трубопроводе. Предлагается 30 вариантов заданных параметров процесса. Возможно моделирование с применением стандартной программы Simulink или на основе самостоятельно разработанной программы. В настоящих указаниях предполагается второй случай.

2. Исходные данные о процессе

m=450 кПа

s = 25 кПа

a = 0.02 с^-1

Примем известными математическое ожидание (среднее значение) m давления P(t) как случайной функции времени t и его корреляционную функцию K(τ). Такое описание процесса является исчерпывающим, если он относится к категории нормальных: любой набор его значений в различные моменты времени образует совокупность нормально распределенных случайных величин. Нормальность процесса далее предполагается и обеспечивается алгоритмом моделирования.

Корреляционная функция процесса K(τ) описывается выражением

K(τ)=s²e^-a|t| , (1)

где s – стандартное (среднее квадратическое) отклонение процесса (кПа),

а a - параметр, измеряемый в 1/с и характеризующий степень убывания корреляционной функции по мере увеличения ее аргумента τ. Последний означает интервал времени между двумя значениями процесса и исчисляется в секундах.Наряду с приведенными используются следующие понятия.

Центрированный процесс 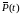, получающийся из исходного вычитанием из его значений математического ожидания:

=P(t) – m. (2)

Дисперсия процесса D, равная квадрату стандартного отклонения:

D = s². (3)

Коэффициент вариации v – отношение стандартного отклонения к математическому ожиданию:

v = s/m. (4)

Коэффициент вариации часто выражают в процентах; тогда к отношению в правой части добавляется множитель 100.

Нормированная корреляционная функция (НКФ) ρ(τ), получаемая путем деления K(τ) на дисперсию

ρ(τ) = K(τ)/D. (5)

Кроме того, будет использован показатель, обычно именуемый интервалом корреляции τ_кор – значение τ, по достижении которого корреляционная функция не выходит более из «коридора» 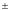0.01s². Для корреляционной функции вида (1) приближенное значение τ_кор составляет

τ_кор = 5/a. (6)

Параметры a или τ_кор позволяют судить о степени хаотичности или, напротив, регулярности процесса: чем больше a (чем меньше τ_кор), тем хаотичнее поведение процесса, ,степень его изменчивости на выделенных промежутках времени.

При подстановке исходных данных получаем следующие значения:

K(τ)=s²e^-a|t| K(τ)=625 e^-0.02|t| K(τ)= 4.21

D = s ². D =625

v = s/m. v=0.05

τ_кор = 5/a. τ_кор = 250

ρ(τ) = K(τ)/D. ρ(τ) = 0.007