Система Уолша–Адамара

Рассмотренные в п. 1.6 функции Уолша задавались целочисленным номером или и аргументом который непрерывно изменялся в интервале Так как функции Уолша кусочно-постоянные на двоичных участках ; ; то для аргумента достаточно указать принадлежность к определенному участку, т. е. можно рассматривать функции Уолша как функции дискретного аргумента или . При таком представлении первым функциям Уолша может быть сопоставлена квадратная матрица Элементами строки этой матрицы являются значения функции Уолша (в нумерации Уолша или Пэли) на двоичных участках. Пример таких матриц в случае п риведён на рис. 1.7.2.

а) б)

Рис. 1.7.2. Функции Уолша, упорядоченные по Уолшу, при

а – непрерывные; б – дискретные

Матрицы ортогональны, т. е.

где – единичная матрица, а верхний индекс означает транспонирование. Элементы строк равны кроме того, матрицы симметричны.

Рассмотрим теперь ещё одну систему функций Уолша – систему Уолша–Адамара. В этой системе функции Уолша расположены одна под другой в таком порядке, что из них образуется матрица Адамара. Для матриц Адамара порядка существует метод итеративного построения на базе элементарной матрицы порядка 2:

С троки матрицы Адамара представляют значения функций Уолша, расположенных в порядке Адамара (рис. 1.7.3).

а) б)

Рис. 1.7.3. Функции Уолша, упорядоченные по Адамару, для

а – непрерывные; б – дискретные

Функции Уолша–Адамара определяются следующим образом:

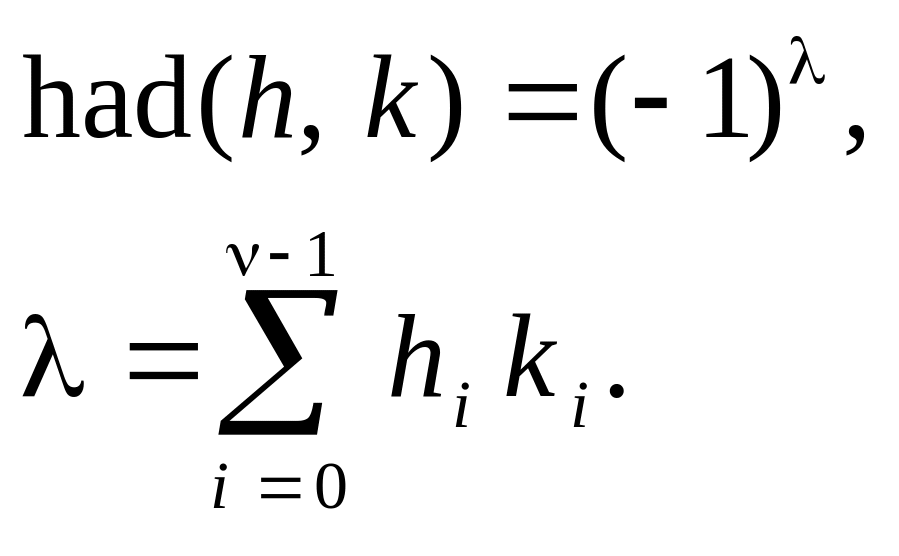
Здесь и – коэффициенты двоичного представления чисел и

Функции ортогональны:

симметричны:

,

N-периодичны по обеим переменным:

Функции Хаара

Система функций Хаара где – безразмерное время и была введена Хааром в 1910 году как полная ортонормированная система функций в На рис. 1.7.4а изображены первые восемь функций Хаара.

б)

Рис. 1.7.4. Функции Хаара при :

а – непрерывные; б – дискретные

а)

Функции Хаара можно получить, используя рекуррентное соотношение [29]:

где

Функции Хаара дискретного аргумента изображены на рис. 1.7.4б. Каждая строка матрицы является дискретной функцией Хаара. Полученные таким образом матрицы используются для дискретного преобразования Хаара и обозначаются где

Функция Хаара является примером материнского вейвлета. Путём целочисленных двоичных растяжений и двухпараметрических сдвигов одной вейвлет-функции образуется ортогональный базис. Сигналы, как элементы гильбертова пространства, анализируются путём разложения по полученным базисным функциям. При обработке сигналов с изменяющимися частотно-временными параметрами (например, речевых сигналов) вейвлет-анализ может оказаться более предпочтительным, чем фурье-анализ. Введение в вейвлет-анализ сигналов рассматривается в п. 1.14.

Вопросы, задачи и упражнения к пп. 1.1–1.7

1. Определить линейное метрическое, нормированное и гильбертово пространства сигналов.

2. Определить линейную зависимость и независимость, а также ортогональность сигналов.

3. Определить обобщенный ряд Фурье.

4. Доказать формулы (1.14), (1.16).

5. Доказать равенство Парсеваля (1.17).

6. Пространство 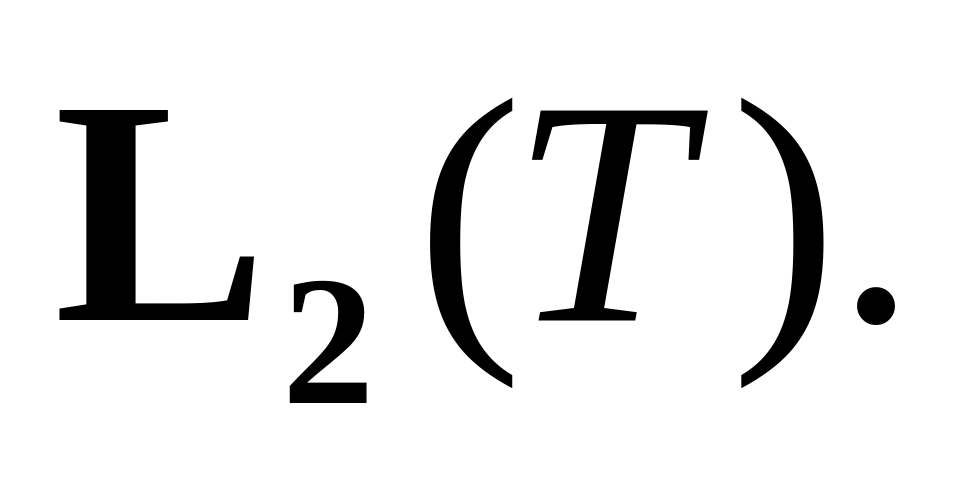Определение и примеры. Ряды Фурье в Среднеквадратичная метрика.

7. Множество М состоит из прямоугольных видеоимпульсов длительностью  и амплитудой А. Образует ли множество М линейное пространство?

8. Пусть система линейно независимых функций в Обозначим через линейное подпространство, натянутое на эти функции. Показать, что представление

единственно вследствие линейной независимости базисных функций.

9. Используя неравенство Коши–Буняковского 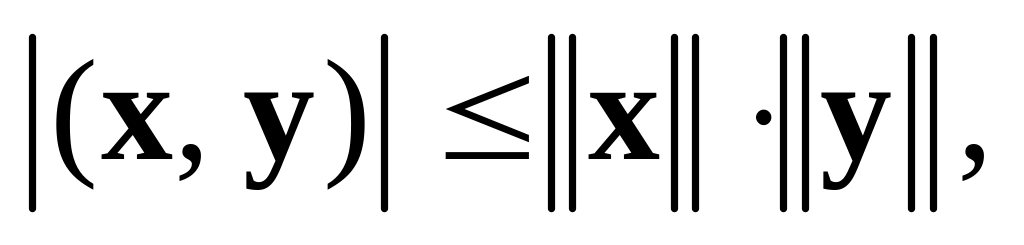доказать, что среднее значение действительной периодической функции всегда меньше или равно её среднеквадратическому значению:

10. Автокорреляционная функция действительного периодического процесса определяется следующим выражением:

Используя неравенство Коши–Буняковского доказать, что

11. Сигнал представляет собой несимметричный треугольный импульс амплитудой и длительностью Вычислить энергию и норму такого сигнала.

12. Вычислить энергию и норму радиоимпульса, содержащего периодов косинусоидальной функции

Рассмотреть случай

13. Имеются два сигнала:

где – прямоугольная функция длительностью и единичной амплитудой. Выбрать амплитуду так, чтобы расстояние между двумя сигналами было минимальным.

14. Пусть – вещественное гильбертово пространство, содержащее сигналы x и y. Доказать, что имеет место равенство параллелограмма

15. Доказать минимальное свойство коэффициентов Фурье.

16. Пространство сигналов Определение и примеры. Ряды Фурье в Среднеквадратичная метрика.

17. Практический смысл полноты ортогональной системы. Равенство Парсеваля в нормированном и ненормированном базисе.

18. Пусть полная ортонормированная система в Для любых из проверить равенство Парсеваля:

19. Функции отсчетов. Определение и основные свойства. Доказать ортогональность функций отсчетов на бесконечном интервале

20. Комплексные экспоненциальные функции и их основные свойства.

21. Функции Уолша. Основные свойства. Построить первые восемь функций системы Уолша.

22. Построить первые восемь функций системы Уолша–Пэли.

23. Матрицы Адамара. Построить первые восемь функций системы Уолша–Адамара.

24. Дискретные экспоненциальные функции (ДЭФ). Основные свойства.

25. Построить матрицу ДЭФ размером с минимальными фазами.

26. Взаимосвязь номеров функций Уолша в нумерации Уолша, Пэли и Адамара.

27. Для линейно изменяющегося сигнала найти первые четыре коэффициента Фурье по системе Уолша. Найти среднеквадратичную ошибку представления такого сигнала четырьмя первыми членами ряда Уолша–Фурье.

28. Сигнал представляет собой симметричный треугольный импульс с амплитудой А и длительностью 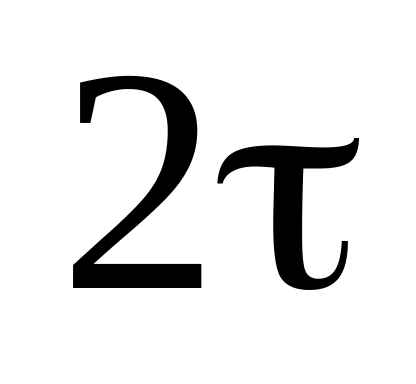. Сигнал прямоугольной формы вписан в треугольный. Найти амплитуду при которой расстояние между двумя сигналами будет минимальным. Рассмотреть три метрики (1.1), (1.2), (1.3).

29. С использованием среднеквадратичной метрики определить взаимные расстояния между любыми двумя функциями из совокупности первых четырех: а) функций Уолша; б) функций ДЭФ, в) функций Хаара.

30. Построить первые 16 функций Хаара.

31. Изобразить матрицу, соответствующую первым 16 функциям Хаара дискретного аргумента.