1.3. Примеры пространств сигналов Пространство
Элементами множества
являются в общем случае комплексные
функции
заданные на интервале
конечном или бесконечном. Будем считать,
что функции
являются функциями с интегрируемым
квадратом
Этот
интеграл обычно трактуется как энергия
сигнала, если принять, что
это ток или напряжение на сопротивлении
При этом является пространством с ограниченной энергией. Все физические сигналы имеют конечную энергию.
В скалярное произведение, норма и расстояние определяются соответственно
Метрика
называется среднеквадратичной метрикой
и определяет среднеквадратичное
отклонение сигнала
от
Условие
ортогональности двух векторов
и
в
записывается в виде
Обобщенный ряд Фурье (1.2.13) в принимает вид
где
есть коэффициенты Фурье по системе {n}.
Пространство
Элементами множества
являются последовательности чисел (в
общем случае комплексные)
удовлетворяющие
условию
Такие последовательности называют также счётномерными векторами. В данном классе последовательностей вводят операции сложения векторов и умножения их на скаляр:
Скалярное произведение, норма и расстояние определяются соответственно
Эти
соотношения определяют пространство
которое можно рассматривать как
координатную реализацию гильбертова
пространства
Обратимся
к формулам обобщенного ряда Фурье
(1.2.13) – (1.2.16). Эти формулы устанавливают
взаимно однозначное соответствие
(изоморфизм)
между сигналом и совокупностью его
коэффициентов Фурье. Сигнал
является элементом пространства
а совокупность коэффициентов Фурье
(счетномерный вектор) – элементом
пространства
Между
пространствами
и
устанавливается изометрия, при которой
сохраняется норма элементов пространств
и
(1.2.18).
Пространство
Ограничение
размерности векторов до
координат
приводит к пространству
которое является подпространством
комплексного гильбертова пространства
Характерно, что в
существуют
линейно независимых векторов
Эти
векторов называют базисом N-мерного
пространства.
Обобщенный
ряд Фурье в пространстве
с ортогональным базисом
принимает вид
где
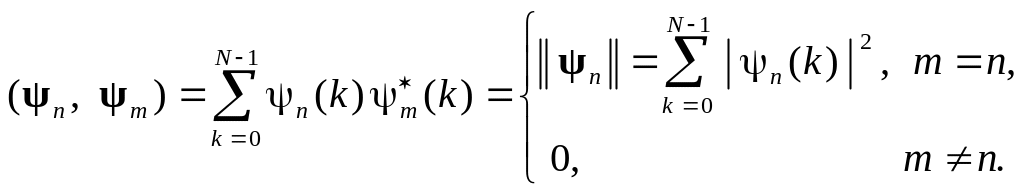
Пример 1.3.1. В качестве базисной системы в рассмотрим дискретные экспоненциальные функции (ДЭФ) (см. п. 1.7):
В
этой формуле
и
принимают целочисленные значения,
т.
е. число функций в системе равно числу
отсчетов каждой функции. Вследствие
этого, а также в силу линейной независимости,
система ДЭФ является полной в пространстве
Функции (ДЭФ) ортогональны:
Поэтому ряд Фурье по этой системе
где коэффициенты Фурье
Соотношения
и определяют пару дискретного
преобразования Фурье (ДПФ),
которое будет рассмотрено в главе 3.
Отличительной особенностью ДПФ является
то, что сигнал и его спектр определяются
на конечных и равных интервалах
Последовательности
и
–
периодические (с периодом
)
функции дискретного аргумента. Это
объясняется N-периодичностью
базисных функций ДПФ по обоим аргументам.
При этом меняется привычное понятие
сдвига, а именно: сдвиг сигнала и его
спектра на интервале
понимается как циклическая перестановка
отсчетов (часть сигнала или его спектра,
выходящая за пределы интервала
с одного конца, вставляется в этот
интервал с другого конца). При циклическом
сдвиге значения индексов k
и n
отсчитываются по модулю