
- •Г л а в а 1. Математические основы обработки сигналов
- •1.1. Классификация сигналов
- •1.2. Пространства сигналов Метрические пространства
- •Линейные пространства
- •Гильбертово пространство
- •1.3. Примеры пространств сигналов Пространство
- •Пространство
- •Пространство
- •1.4. Представление сигналов ортогональными рядами. Общий метод дискретизации
- •1.5. Обобщённые ряды Фурье. Полные ортонормированные системы
- •1.6. Некоторые системы базисных функций из l2
- •Функции отсчётов
- •Импульсные базисные функции
- •Комплексные экспоненциальные функции
- •Функции Уолша
- •1.7. Некоторые базисные системы из
- •Система единичных импульсов
- •Дискретные экспоненциальные функции (дэф)
- •Система Уолша–Адамара
- •Функции Хаара
- •Вопросы, задачи и упражнения к пп. 1.1–1.7
- •1.8. Спектральный метод анализа линейных систем
- •1.8.1. Преобразование Фурье. Основные свойства
- •Свойства спектральной плотности
- •Основные спектральные теоремы
- •1) Свойство линейности (спектр суммы равен сумме спектров)
- •1.8.2. Импульсные воздействия в линейных системах
- •1.8.3. Спектры импульсных сигналов Спектр одиночного прямоугольного импульса
- •Спектр симметричного треугольного импульса
- •Спектр косинусоидального импульса
- •С пектр одностороннего экспоненциального импульса
- •Спектр двустороннего экспоненциального импульса
- •Спектр колокольного импульса
- •Спектр короткого одиночного импульса
- •Связь между длительностью импульса и шириной его спектра
- •1.8.4. Дельта-функция и её спектр
- •Производные от дельта функций
- •1.8.5. Спектры некоторых неинтегрируемых сигналов Спектр действительного гармонического сигнала
- •Спектр функции включения
- •Спектр функции знака
- •1.8.6. Примеры нахождения спектров Спектр сигнала на выходе интегратора
- •Спектр отрезка синусоиды
- •Спектр пачки равноотстоящих импульсов
- •Сводка основных свойств пф
- •1.9. Спектры периодических сигналов Спектр гармонического сигнала
- •Спектр t-периодического сигнала
- •Спектр периодической последовательности дельта-функций
- •Спектральная функция периодической последовательности прямоугольных импульсов
- •Задачи и упражнения к пп. 1.8–1.9
- •1.10. Преобразование Лапласа в линейных системах
- •1.10.1. Теорема разложения Хевисайда
- •Кратные полюсы
- •1.10.2. Применение преобразования Лапласа для анализа цепей
- •1.11. Динамическое представление сигналов
- •Задачи и упражнения к п. 1.11
- •1.12. Представление колебаний в комплексной форме Комплексная огибающая
- •Спектр комплексной огибающей
- •Аналитический сигнал. Преобразование Гильберта
- •Некоторые свойства преобразования Гильберта
- •Упражнения и задачи к п. 1.12
- •1.13. Преобразование Хартли
- •Примеры вычисления преобразования Хартли
- •Упражнения и задачи к п. 1.13
- •1.14. Введение в вейвлет-анализ сигналов
- •От анализа Фурье к вейвлет-анализу
- •Признаки вейвлета
- •Примеры материнских вейвлетов
- •Вейвлет-преобразование (вп)
- •Свойства вейвлет преобразования
- •Частотно-временная локализация вп
- •Вейвлет-ряды
- •Дискретное вейвлет-преобразование
- •Пример вейвлет преобразования
Задачи и упражнения к п. 1.11
Ё

 мкость
мкость
 и сопротивление
соединённые последовательно, подключаются
при
к источнику ЭДС в виде линейно
изменяющегося напряжения
и сопротивление
соединённые последовательно, подключаются
при
к источнику ЭДС в виде линейно
изменяющегося напряжения
 Найти и изобразить закон изменения
выходного напряжения
Найти и изобразить закон изменения
выходного напряжения
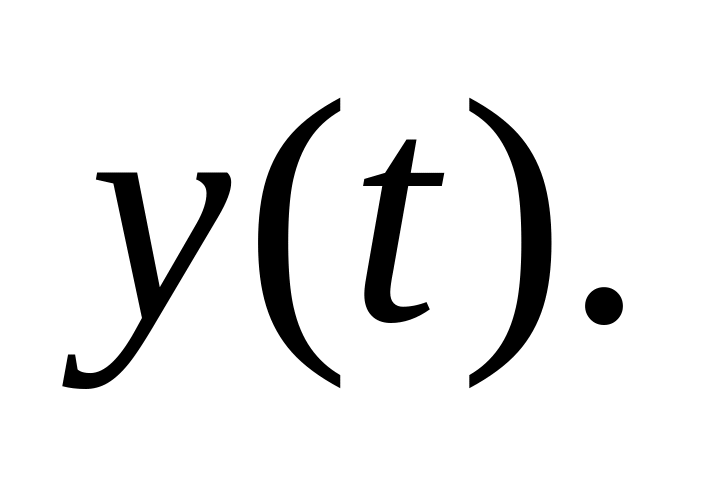 Поменять местами ёмкость и сопротивление
и проделать то же самое. Отметить влияние
постоянной времени
Поменять местами ёмкость и сопротивление
и проделать то же самое. Отметить влияние
постоянной времени
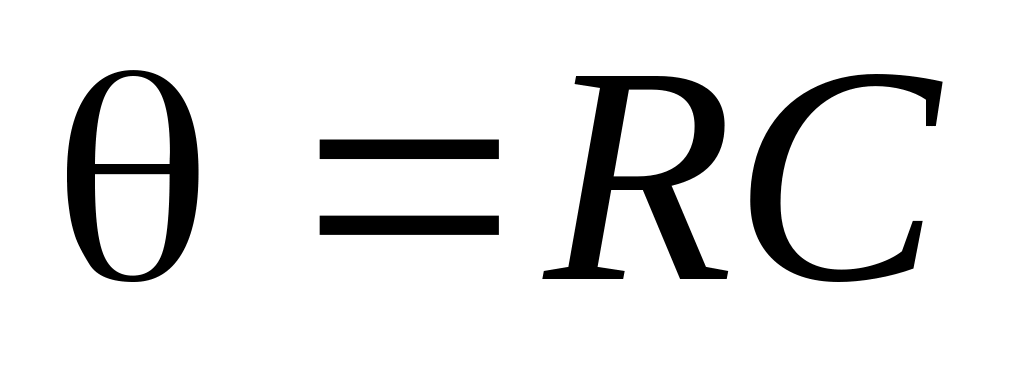 и коэффициента наклона
на вид выходного напряжения.
и коэффициента наклона
на вид выходного напряжения.С

 опротивление
и ёмкость
соединённые последовательно, подключаются
при
к источнику ЭДС
в виде симметричного треугольного
импульса. Определить ток в цепи при
опротивление
и ёмкость
соединённые последовательно, подключаются
при
к источнику ЭДС
в виде симметричного треугольного
импульса. Определить ток в цепи при
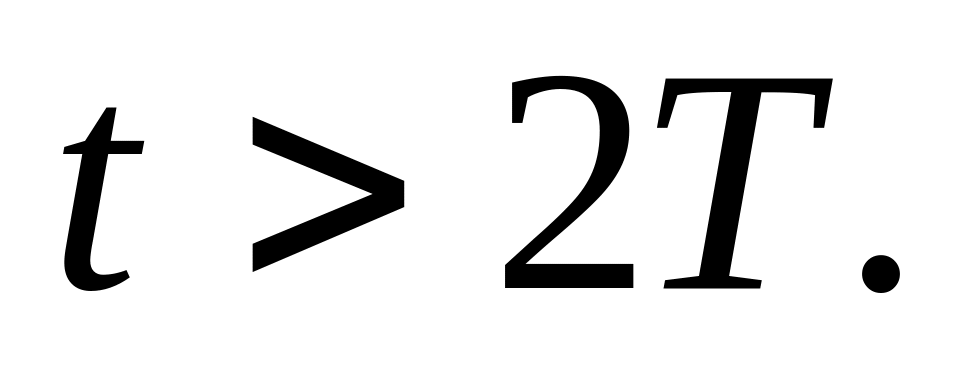
Сопротивление
 и индуктивность
и индуктивность
 соединённые последовательно, подключаются
при
к источнику ступенчатой ЭДС, показанной
на рисунке. Определить ток в цепи при
соединённые последовательно, подключаются
при
к источнику ступенчатой ЭДС, показанной
на рисунке. Определить ток в цепи при
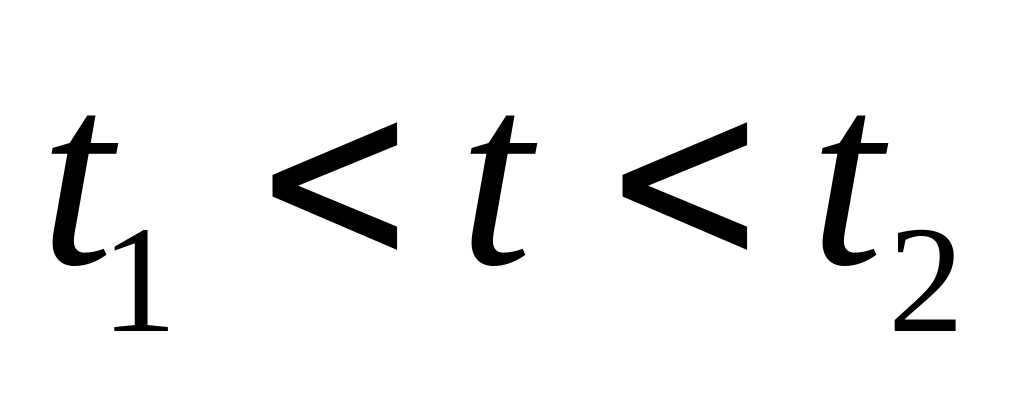 и
и
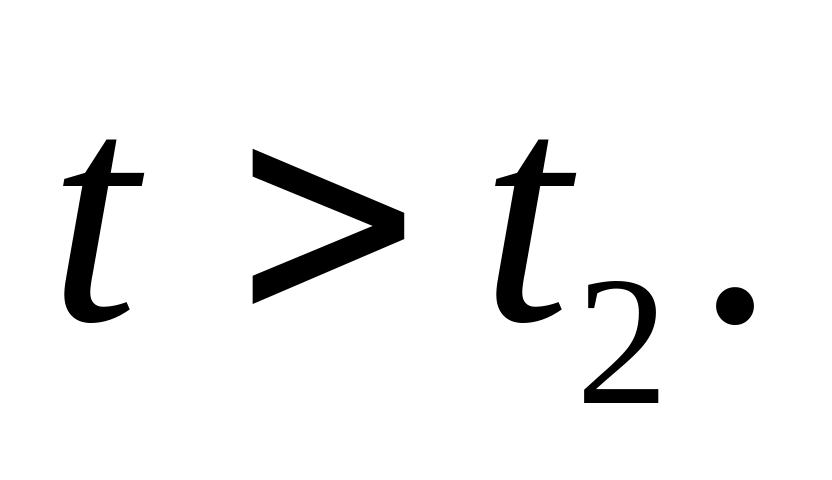
Сопротивление и индуктивность соединённые последовательно, подключаются при к источнику ЭДС
 Определить ток в цепи при
Определить ток в цепи при
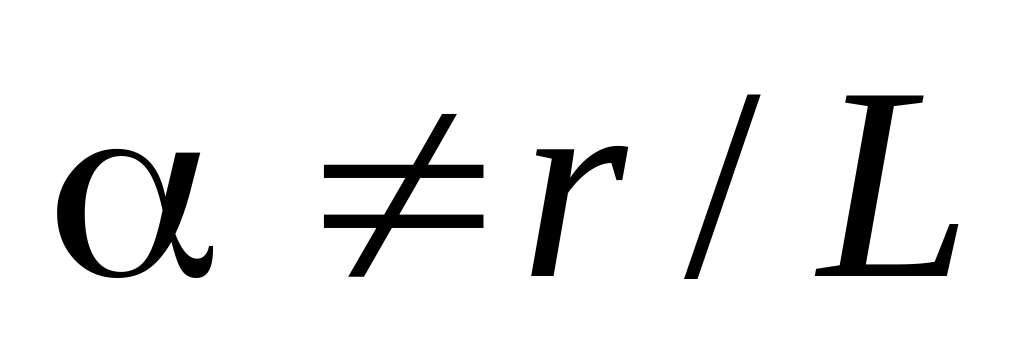 и
и

О т в е т:
![]()
Решить предыдущую задачу, если ЭДС равна

О т в е т:
![]()
а
 )
Найти с помощью свёртки переходную
характеристику
системы, импульсная характеристика
которой
показана на рисунке.
)
Найти с помощью свёртки переходную
характеристику
системы, импульсная характеристика
которой
показана на рисунке.
б) Проверить
полученный результат, исходя из того,
что
![]()
в) Построить блок-схему фильтра по его импульсной характеристике.
П
 усть
усть
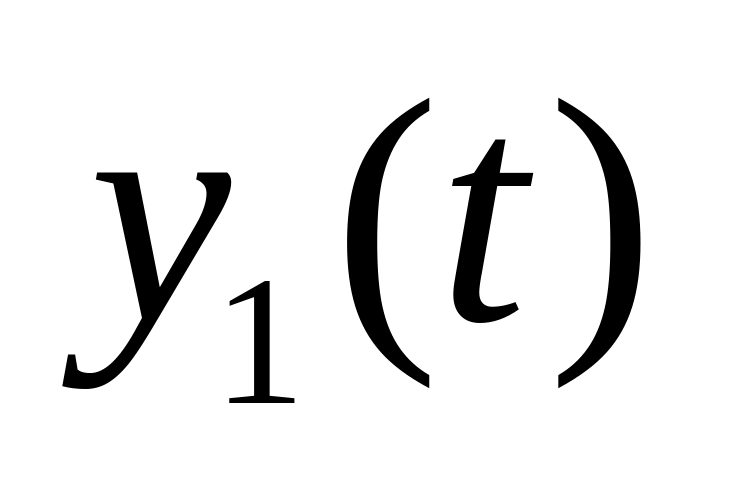 –
реакция ЛИВС на воздействие
–
реакция ЛИВС на воздействие

а) Найти импульсную характеристику системы.
б) Найти реакцию
![]() на воздействие
на воздействие
![]()
О
 пределить
пределить
 при
при
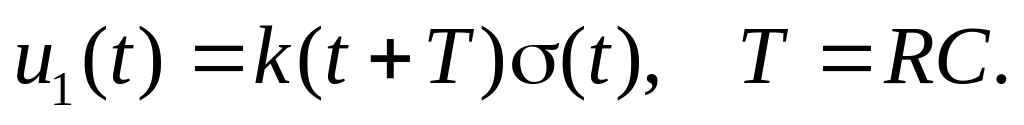
Определить переходную характеристику идеального фильтра нижних частот и с её помощью проиллюстрировать явление Гиббса.
1.12. Представление колебаний в комплексной форме Комплексная огибающая
Р ассмотрим
узкополосное колебание, у которого
спектр ограничен полосой частот
ассмотрим
узкополосное колебание, у которого
спектр ограничен полосой частот![]() ,
причем
,
причем
![]() (рис. 1.12.1).
(рис. 1.12.1).
Рис. 1.12.1
Наиболее общая форма записи узкополосного колебания имеет вид
![]()
где
![]() и
и
![]() – медленно меняющиеся по сравнению с
циклическим множителем функции времени.
Гармонический сигнал (косинусоида с
постоянной частотой
и начальной фазой
– медленно меняющиеся по сравнению с
циклическим множителем функции времени.
Гармонический сигнал (косинусоида с
постоянной частотой
и начальной фазой![]() )
подвергается одновременно амплитудной
и фазовой модуляции. Так, в случае строгой
амплитудной модуляции гармонического
сигнала дисперсионность среды
распространения производит частичное
преобразование амплитудных изменений
в фазовые. Узкополосные сигналы можно
считать квазигармоническими
их амплитуда и фаза медленно изменяются
во времени.
)
подвергается одновременно амплитудной
и фазовой модуляции. Так, в случае строгой
амплитудной модуляции гармонического
сигнала дисперсионность среды
распространения производит частичное
преобразование амплитудных изменений
в фазовые. Узкополосные сигналы можно
считать квазигармоническими
их амплитуда и фаза медленно изменяются
во времени.
Комплексное представление полосовых сигналов является прямым развитием известного символического метода, позволяющего представлять гармоническое колебание как действительную или мнимую часть комплексной функции:
![]()
Число
![]() называют комплексной амплитудой
гармонического колебания.
называют комплексной амплитудой
гармонического колебания.
В соответствии с полосовой радиосигнал представляет собой сложное колебание, получающееся из гармонического сигнала с частотой при одновременной его модуляции как по амплитуде, так и по фазе. Мы попытаемся корректно распространить символический метод на такие колебания. Для этого представим в виде
![]()
Здесь
![]() и
и
![]()
называются
квадратурными
составляющими
узкополосного колебания
соответственно
![]() − синфазная, а
− синфазная, а
![]() − квадратурная компоненты. Квадратурные
составляющие являются низкочастотными
действительными функциями и несут всю
информацию о модуляции сигнала. Спектры
этих функций сконцентрированы возле
начала координат в полосе
− квадратурная компоненты. Квадратурные
составляющие являются низкочастотными
действительными функциями и несут всю
информацию о модуляции сигнала. Спектры
этих функций сконцентрированы возле
начала координат в полосе
![]()
К вадратурные
компоненты могут быть получены в
следующей схеме.
вадратурные
компоненты могут быть получены в
следующей схеме.
Рис. 1.12.2. Получение квадратурных компонент узкополосного колебания
Действительно, после умножения на сигнал когерентного гетеродина в верхнем канале имеем
![]()
Высокочастотные
составляющие вблизи
![]() подавляются фильтром нижних частот
(ФНЧ) и на выходе верхнего канала остается
синфазная компонента
подавляются фильтром нижних частот
(ФНЧ) и на выходе верхнего канала остается
синфазная компонента
![]() Аналогично в нижнем канале выделяется
квадратурная компонента
Аналогично в нижнем канале выделяется
квадратурная компонента
![]()
В реальных формирователях квадратур предъявляются высокие требования к идентичности, линейности и стабильности амплитудных характеристик каналов, а также к точному соблюдению 90 сдвига фаз между гармоническими колебаниями когерентного гетеродина.
Амплитудную и фазовую модуляции сигнала можно определить с помощью квадратурных компонент. Из имеем
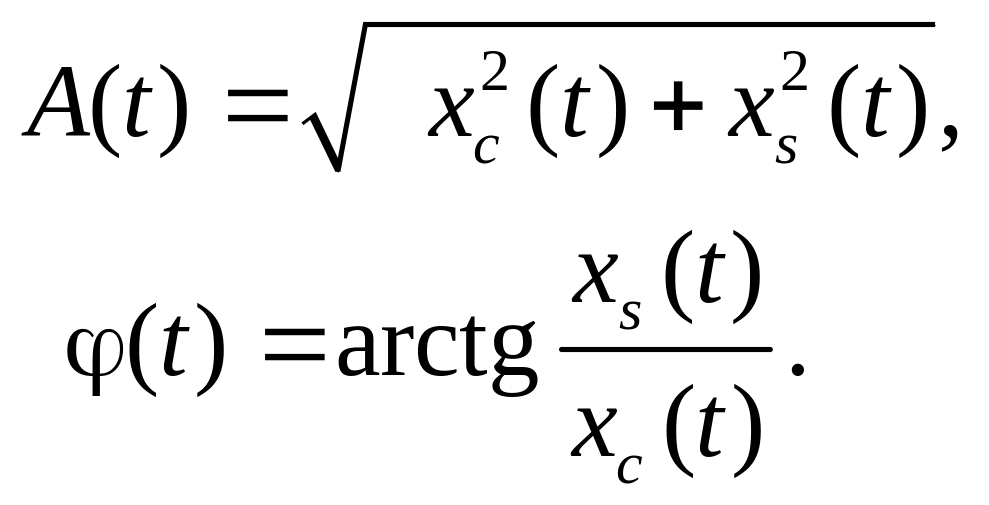
Ветвь арктангенса выбирается таким образом, чтобы была непрерывной функцией времени.
Введём комплексную огибающую
![]()
Эта функция содержит всю обусловленную модуляцией информацию. При этом физическая огибающая равна
![]()
Полная фаза узкополосного колебания
![]()
а мгновенная частота определяется как производная по времени от полной фазы:

Комплексную
огибающую можно представить на комплексной
плоскости вектором, который совершает
некоторое сложное движение, изменяясь
как по модулю, так и по направлению (рис.
1.12.3). Исходный действительный сигнал
связан с комплексной огибающей
![]() соотношением
соотношением
![]()

Таким образом, понятие комплекс-ной огибающей обобщает понятие комплексной амплитуды на случай узкополосных радиосигналов.
Рис. 1.12.3
