1.8.5. Спектры некоторых неинтегрируемых сигналов Спектр действительного гармонического сигнала

Используя формулу Эйлера и соотношение , можем записать

Таким образом, модуль спектра действительного гармонического сигнала с частотой и амплитудой представляет собой пару дельта-функций с весом расположенных на частотах Для частоты соответствие записывается в виде

Спектр функции включения

Функция была определена соотношениями – . Возьмём функцию где параметр выбирается так, чтобы функция была абсолютно интегрируемой, т. е.

Тогда

Следовательно:

Переход к пределу справедлив при всех частотах, кроме

С другой стороны, функция включения имеет постоянную составляющую поэтому можем записать окончательно:

Рис. 1.8.10

Действительная и мнимая части спектра функции включения изображены на рис. 1.8.10.

Спектр функции знака

Эта функция определяется выражением

Е ё связь с функцией включения поясняет рис. 1.8.11.

Рис. 1.8.11

Видно, что Отсюда окончательно

Спектр чисто мнимый, как у всякой нечётной функции.

1.8.6. Примеры нахождения спектров Спектр сигнала на выходе интегратора

Упражнение 1.8.1. Найдём спектр функции

Представим интеграл в виде свёртки:

По теореме о спектре свёртки с учётом можем написать

Упражнение 1.8.2. Определить спектральную плотность сигнала на выходе реального интегратора

Здесь – фиксированный параметр. Этот определённый интеграл равен разности двух значений первообразной: одно при аргументе а другое – при аргументе

Используя спектр первообразной и теорему запаздывания, получаем

Здесь – оператор задержки на . Модуль знаменателя линейно растёт с частотой, а величина ограничена по модулю. Поэтому интегратор подобно фильтру нижних частот ослабляет высокие частоты в спектре входного сигнала

Спектр отрезка синусоиды

Упражнение 1.8.3. Определим спектр отрезка синусоиды, состоящего из целого числа периодов:

где – целое. Представим в виде

Здесь а – симметричный прямоугольный импульс длительностью и амплитудой 1. Мы уже знаем, что

и .

По теореме о спектре произведения можем записать

Для случая (два периода синуса) на рис. 1.8.12 изображены смещённые ядра Дирихле и и модуль результирующего спектра

Рис. 1.8.12. Спектр отрезка из двух периодов синусоиды

Как видно, боковые лепестки смещённых ядер, примыкающие к началу координат, синфазно складываются, в результате спектр отрезка синусоиды при является ассиметричным: левый лепесток больше правого. Для отрезка косинусоиды, наоборот, правый лепесток будет больше левого.

Спектр пачки равноотстоящих импульсов

У пражнение 1.8.4. Найдём спектр пачки равноотстоящих импульсов. Для определённости возьмём пачку из прямоугольных импульсов (рис. 1.8.13).

Рис. 1.8.13

Обозначим через спектральную плотность первого импульса. Тогда для группы из равноотстоящих импульсов в соответствии с теоремой запаздывания будем иметь

На частотах , где – целое, каждое слагаемое в квадратных скобках равно единице, следовательно:

Таким образом, на частотах модуль спектра пачки в раз больше модуля спектра одиночного импульса. Это объясняется тем, что на частотах спектральные компоненты различных импульсов складываются с фазовыми сдвигами, кратными

Суммируя членов геометрической прогрессии, получаем

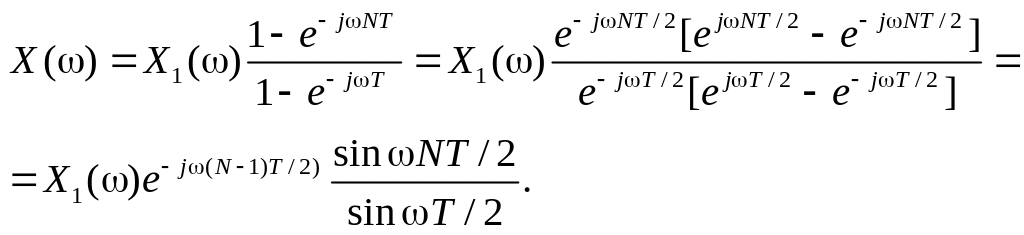
Видно, что на частотах где – целое, Подставляя сюда значение

где – длительность отдельного импульса, получаем окончательно для спектра пачки из равноотстоящих прямоугольных импульсов:

Для иллюстрации на рис. 1.8.14а изображён модуль спектра пачки из трёх прямоугольных импульсов, а на рис. 1.8.14б – из четырёх. При этом интервал между соседними импульсами Пунктиром изображён модуль спектра одиночного импульса. С увеличением числа импульсов в пачке спектральная плотность при принимает дискретную структуру спектра периодической функции (рис. 1.9.2).

Нетрудно обобщить этот результат на произвольную форму одиночного импульса.

Рис. 1.8.14. Модуль спектра пачки прямоугольных импульсов:

а – три импульса в пачке, б – четыре импульса в пачке

В заключении этого параграфа приведём сводку основных свойств преобразования Фурье. Их можно рассматривать как задачи и упражнения для самостоятельной работы.