1.8.4. Дельта-функция и её спектр

Введём в рассмотрение дельта-функции Дирака. Их корректное определение даётся в теории обобщённых функций [5–7]. Здесь мы воспользуемся некоторыми полезными свойствами этих функций.

Дельта-функция Дирака по определению равна бесконечности, когда её аргумент равен нулю, и нулю – при остальных значениях, причём площадь под её графиком равна единице. Таким образом,

и

Из последнего соотношения следует, что дельта-функция имеет размерность, обратную размерности её аргумента.

Часто желательно определять эту функцию так, чтобы она была чётной функцией своего аргумента:

в этом случае

Предположим, что дельта-функция интегрируема по интервалу

Тогда

где – функция единичного скачка или функция Хевисайда:

Таким образом, функция единичного скачка является интегралом от дельта-функции. Следовательно:

а) б)

Рис. 1.8.9. а – дельта-функция, б – функция единичного скачка

Рассмотрим три импульса (рис. 1.8.10), отличающиеся тем, что площади их равны единице.

Р ис. 1.8.10. Импульсы, обращающиеся в дельта-функцию,

при стремлении их длительности к нулю

Введём предельные соотношения:

Каждая из приведённых аппроксимирующих функций (импульсов) является простым и физически наглядным прототипом дельта-функции. Однако следует отметить, что дельта-функция не является ни функцией в классическом смысле, ни импульсом, а является обобщенной функцией.

Известно так называемое фильтрующее свойство дельта-функции, заключающееся в том, что её свёртка с любой ограниченной и непрерывной в точке функцией равна

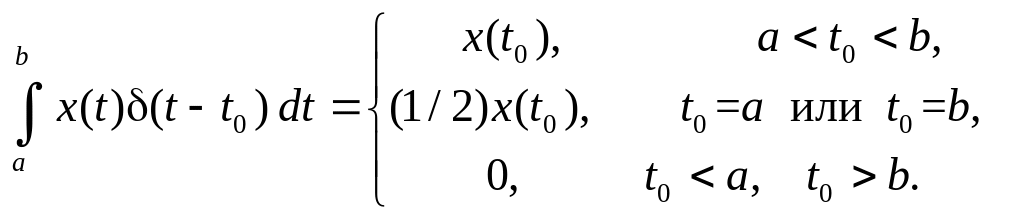
Если функция в точке имеет разрыв (первого рода), то

где – значения справа и слева от точки разрыва.

Доказательство получается, если под знак интеграла подставить вместо любую аппроксимирующую её функцию (рис. 1.8.10), а затем перейти к пределу.

Если – действительная величина, то выполняются следующие равенства:

На основании находим, что

т. е. спектр дельта-функции постоянен на всех частотах. Отсюда еще одно полезное соотношение (обратное ПФ):

Аналогично, из того, что можем записать

Из последних соотношений видно, что спектр единичной константы есть дельта-функция, сосредоточенная в нуле, а спектр комплексной экспоненты – одиночная дельта-функция, сосредоточенная в точке Для частоты соответствие записывается в виде

Производные от дельта функций

Производные от дельта-функции определяются как пределы соответствующих производных от аппроксимирующих функций.

Так, например, в случае гауссовой аппроксимации для n-й производной от дельта-функции получаем следующее определение:

Так же как и сама дельта-функция, её производные равны нулю при Поведение производных при несколько сложнее. Так, например, первая производная

равна при подходе к началу координат слева ( и равна при подходе справа ( Таким образом, в окрестности поведение сравнимо с поведением функции

Фильтрующее свойство дельта-функции распространяется также и на её производные:

Если производная терпит разрыв (первого рода) в точке то

Спектр производной дельта-функции получаем с использованием

Отсюда видно, что если то