7. Причины применения в эвм двоичной системы счисления:

Двоичная система счисления оказалась удобной для использования в ЭВМ. Использование двоичной системы оказалось наиболее эффективным в электронных схемах: цифры 0 и 1 удобно кодировать уровнями напряжения, соответствующим напряжению на шинах питания, „0“ и„+V“; использование большего количества уровней привело бы к усложнению схем. Для предоставления информации используется двоичное кодирование, т.к удалось создать надежно работающие технические устройства способные со стопроцентной надежностью сохранять и распознавать не более двух различных состояний (цифр).

8-10. Алгоритмы перевода чисел из одной позиционной системы исчисление в другую

1. Для перевода чисел из системы исчисления с основой p в систему исчисления с основой q, используя арифметику новой системы исчисления с основой q, нужно записать коэффициенты разложения, основы степеней и показатели степеней в системе с основой q и выполнить все действия в этой самой системе. Очевидно, что это правило удобно при переводе в десятичную систему исчисления. Например:

из шестнадцатеричной в десятичную:

92C816=9*10163+2*10162+C*10161+8*10160= 9*16103+2*16102+12*16101+8*16100=37576

из восьмеричной в десятичную:

7358=7*1082+3*1081+5*1080= 7*8102+3*8101+5*8100=47710

из двоичной в десятичную:

1101001012=1*1028+1*1027+ 0*1026+1*1025+0*1024+0*1023+ 1*1022+0*1021+1*1020= 1*2108+1*2107+0*2106+1*2105+ 0*2104+0*2103+1*2102+0*2101+ 1*2100=42110

2. Для перевода чисел из системы исчисления с основой p в систему исчисления с основой q с использованием арифметики старой системы исчисления с основой p нужно:

для перевода целой части:

последовательно число, записанное в системе основой делить на основу новой системы исчисления, выделяя остатки. Последние записанные в обратном порядке, будут образовывать число в новой системе исчисления;

для перевода дробной части:

последовательно дробную часть умножать на основу новой системы исчисления, выделяя целые части, которые и будут образовывать запись дробной части числа в новой системе исчисления.

Этим же правилом удобно пользоваться в случае перевода из десятичной системы исчисления, поскольку ее арифметика для нас привычна.

Пример: 999,35₁₀=1111100111,01011₂

15. Кодирование информации в эвм.

Кодирование текстовой информации:

Для определения количества информации был найден способ представить любой ее тип (символьный, текстовый, графический) в едином виде, что позволило все типы информации преобразовать к единому стандартному виду. Таким видом стала так называемая двоичная форма представления информации. Она заключается в записи любой информации в виде последовательности только двух символов. Каждая такая последовательность называется двоичным кодом. Недостаток двоичного кодирования – длинные коды. Но в технике легче иметь дело с большим числом простых однотипных элементов, чем с небольшим числом сложных.

С помощью набора битов, можно представить любое число и любой знак. В информационных документах широко используются не только русские, но и латинские буквы, цифры, математические знаки и другие специальные знаки, всего их количество составляет примерно 200-250 символов. Поэтому для кодировки всех указанных символов используется восьмиразрядная последовательность цифр 0 и 1.

Для представления текстовой информации используется таблица нумерации символов или таблица кодировки символов, в которой каждому символу соответствует целое число (порядковый номер). Восемь двоичных разрядов могут закодировать 256 различных символов.

Существующий стандарт ASCII (8 – разрядная система кодирования) содержит две таблицы кодирования – базовую и расширенную. Первая таблица содержит 128 основных символов, в ней размещены коды символов английского алфавита, а во второй таблице кодирования содержатся 128 расширенных символов.

Так как в этот стандарт не входят символы национальных алфавитов других стран, то в каждой стране 128 кодов расширенных символов заменяются символами национального алфавита. В настоящее время существует множество таблиц кодировки символов, в которых 128 кодов расширенных символов заменены символами национального алфавита.

Так, например, кодировка символов русского языка Widows – 1251 используется для компьютеров, которые работают под ОС Windows. Другая кодировка для русского языка – это КОИ – 8, которая также широко используется в компьютерных сетях и российском секторе Интернет.

В настоящее время существует универсальная система UNICODE, основанная на 16 – разрядном кодировании символов. Эта 16 – разрядная система обеспечивает универсальные коды для 65536 различных символов, т.е. в этой таблице могут разместиться символы языков большинства стран мира.

Кодирование графической и звуковой информации :

Для представления графической информации в двоичной форме используется так называемый поточечный способ. На первом этапе вертикальными и горизонтальными линиями делят изображение. Чем больше при этом получилось квадратов, тем точнее будет передана информация о картинке. Как известно из физики, любой цвет может быть представлен в виде суммы различной яркости зеленого, синего, красного цветов. Поэтому информация о каждой клетке должна содержать кодировку значения яркости и количеств зеленого, синего и красного компонентов. Таким образом кодируется растровое изображение – изображение, разбитое на отдельные точки. Объем растрового изображения определяется умножением количества точек на рисунке на информационный объем одной точки, который зависит от количества возможных цветов отображения (для черно-белого изображения информационный объем одной точки равен 1 биту и кодируется двумя цифрами – 0 или 1). Разные цвета и их оттенки получаются за счет наличия или отсутствия трех основных цветов – красного, синего, зеленого и их яркости. Каждая точка на экране кодируется с помощью 4 битов.

Векторное изображение кодируется разбиением рисунка на элементарные отрезки, геометрические фигуры и дуги. Положение этих элементарных объектов определяется координатами точек. Для каждой линии указывается ее тип (сплошная, пунктирная, штрих- пунктирная ), толщина и цвет. Информация о векторном изображении кодируется как обычная буквенно-цифровая и обрабатывается специальными программами.

Режим представления цветной графики в системе RGB с использованием 24 разрядов (по 8 разрядов для каждого из трех основных цветов) называется полноцветным. Для поноцветного режима в системе CMYK необходимо иметь 32 разряда (четыре цвета по 8 разрядов).

Кодирование звуковой информации.

Физически звук представляет собой волновые колебания давления в той или иной среде. Каковы бы ни были физические характеристики колебаний, в данном случае важно то, что звук представляет собой нечто неделимое на части (непрерывное), пробегающее в пространстве и времени. Чтобы записать звук на какой-нибудь носитель можно соотнести его уровень (силу) с какой-нибудь измеряемой характеристикой этого носителя. Так, например, степень намагниченности магнитной ленты в различных ее местах зависит от особенностей звука, который на нее записывался. Намагниченность может непрерывно изменяться на протяжении ленты, подобно тому, как параметры звука могут меняться в воздухе. Т.е. магнитная лента прекрасно справляется с задачей хранения звука. И хранит его в так называемой аналоговой форме, когда значения изменяются непрерывно (плавно), что близко к естественному звуку.

Но как хранить звук на компьютере. Здесь любая информация представлена в цифровой форме. Данные должны быть представлены числами, а, следовательно, информация в компьютере дискретна (разделена). Для того, чтобы записать звук на цифровой носитель информации (например, жесткий диск), его подвергают так называемой оцифровке, механизм которой заключается в измерении параметров звука через определенные промежутки времени (очень малые).

Дискретизация и квантование

При преобразовании звуковой информации в цифровую форму ее подвергают дискретизации и квантованию. Дискретизация заключается в замерах величины аналогового сигнала огромное множество раз в секунду. Полученной величине аналогового сигнала сопоставляется определенное значение из заранее выделенного диапазона: 256 (8 бит) или 65536 (16 бит). Глубина кодирования звука - это количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука.

Если известна глубина кодирования, то количество уровней громкости цифрового звука можно рассчитать по формуле N = 2I. Пусть глубина кодирования звука составляет 16 битов, тогда количество уровней громкости звука равно:

N = 2I = 216 = 65 536.

В процессе кодирования каждому уровню громкости звука присваивается свой 16-битовый двоичный код, наименьшему уровню звука будет соответствовать код 0000000000000000, а наибольшему - 1111111111111111. Привидение в соответствие уровня сигнала определенной величине диапазона и есть квантование.

Понятно, что как бы часто мы не проводили измерения, все равно часть информации будет теряться. Однако и понятно, что чем чаще мы проводим замеры, тем точнее будет соответствовать цифровой звук своему аналоговому оригиналу.

Также, чем больше бит отведено под кодирование уровня сигнала (квантование), тем точнее соответствие.

С другой стороны, звук хорошего качества будет содержать больше данных и, следовательно, больше занимать места на цифровом носителе информации.

В качестве примера можно привести такие расчеты. Для записи качественной музыки аналоговый звуковой сигнал измеряют более 44 000 раз в секунду и квантуют 2 байтами (16 бит дает диапазон из 65536 значений). Т.е. за одну секунду записывается 88 000 байт информации. Это равно (88 000 / 1024) примерно 86 Кбайт. Минута обойдется уже в 5168 Кбайт (86*60), что немного больше 5 Мб.

16. Формы и форматы представления числовых данных в ЭВМ - естественная, нормальная форма, порядок, характеристика.

В форме с фиксированной запятой в разрядной сетке выделяется строго определенное число разрядов для целой и для дробной частей числа. Левый (старший) разряд хранит признак знака (0 – "+", 1 – "-") и для записи числа не используется.

Сама запятая никак не изображается, но ее место строго фиксировано и учитывается при выполнении всех операций с числами. Независимо от положения запятой в машину можно вводить любые числа, т.к.

A = [A] · KА,

где А – произвольное число, [A] – машинное изображение числа в разрядной сетке, KА - масштабный коэффициент.

Естественная форма числа в неявном, условном виде реализуется формулой:

т.е. число записывается только с помощью набора значащих цифр xj без явного указания их весов и знаков сложения между ними. Отсчет ведется от точки, которая обычно фиксируется между целой и дробной частями числа.

С фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной(например, 32,54; 0,0036; –108,2). Форма представления чисел с фиксированной запятой упрощает аппаратную реализацию ЭВМ, уменьшает время выполнения машинных операций, однако при решении задач на машине необходимо постоянно следить за тем, чтобы все исходные данные, промежуточные и окончательные результаты находились в допустимом диапазоне представления. Если этого не соблюдать, то возможно переполнение разрядной сетки, и результат вычислений будет неверным. От этих недостатков в значительной степени свободны ЭВМ, использующие форму представления чисел с плавающей точкой, или нормальную форму. В современных компьютерах форма представления чисел с фиксированной запятой используется только для целых чисел.

Нормальная форма

С плавающей запятой (ПЛЗ) числа изображаются в виде:

X = ± M×P ±r,

где M - мантисса числа (правильная дробь в пределах 0,1 ≤ M < 1), r - порядок числа (целое), P - основание системы счисления. Например, приведенные выше числа с фиксированной запятой можно преобразовать в числа с плавающей запятой так: 0,3254×102, 0,36×10-2, –0,1082×103.

Нормализованная экспоненциальная запись числа - это запись вида a= m*Pq, где q - целое число (положительное, отрицательное или ноль), а m - P-ичная дробь, у которой целая часть состоит из одной цифры. При этом m - мантиссa числа, q - порядк числа.

Tо есть нормальная форма реализуется формулой:

Нормальная форма представления имеет огромный диапазон чисел и является основной в современных ЭВМ.

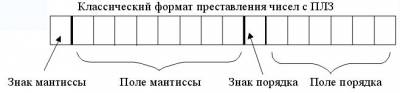
При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды - для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы. Для того, чтобы не хранить знак порядка, используется так называемый смещённый порядок, который рассчитывается по формуле 2(a-1) + ИП, где a - количество разрядов, отводимых под порядок, ИП - истинный порядок.

В конкретной ЭВМ диапазон представления чисел с плавающей запятой зависит от основания системы и числа разрядов для представления порядка. При этом у одинаковых по длине форматов чисел с плавающей запятой с увеличением основания системы счисления существенно расширяется диапазон представляемых чисел. Точность вычислений при использовании формата с плавающей запятой определяется числом разрядов мантиссы. Она увеличивается с увеличением числа разрядов.

Алгоритм представления числа с плавающей запятой:

• перевести число из p-ичной системы счисления в двоичную;

• представить двоичное число в нормализованной экспоненциальной форме;

• рассчитать смещённый порядок числа;

• разместить знак, порядок и мантиссу в соответствующие разряды сетки.

При представлении информации в виде десятичных многоразрядных чисел каждая десятичная цифра заменяется двоично-десятичным кодом. Для ускорения обмена информацией, экономии памяти и удобства операций над десятичными числами предусматриваются специальные форматы их представления: зонный (распакованный) и упакованный. Зонный формат используется в операциях ввода-операций. Для этого в ЭВМ имеются специальные команды упаковки и распаковки десятичных чисел.

Пример записи числа в нормальной форме:

A = 7D08,816

B = -7D08,816

mA = 0,7D088 PxA = 40+4 = 44

mB = -0,7D088 PxB = 40+4 = 44

A = 0 100 0100 0111 1101 0000 1000 1000 0000 A = 44D0880 > 0

B = 1 100 0100 0111 1101 0000 1000 1000 0000 B = C4D0880 < 0