
- •Вариант 1.
- •1. Сформулювати та доказати узагальнену формулу Байєса
- •2. Математичне очікування та дісперсія процесу Пуассона дорівнюють відповідно.
- •3. Оцінити наступну ймовірність
- •Вариант 2.
- •1. Описати зв'язок потіка Ерланга з пуассонівським процесом.
- •3. Нехай – незалежні однаково розподілені випадкові величини з для деякого . Нехай позначає їх часткові суми. Показати, що
- •Вариант 3.
- •1. Описати прорідження пуассонівського потоку вимог.
- •2. Для процесу Пуассона є вірним твердження:
- •3. Нехай - рішення рівняння
- •Вариант 4.
- •1. Знайти оптимальне управління та ціну в задачі р. Мертона у термінальному випадку.
- •2. Формула Іто використовується для:
- •3. Припустимо, що є рішенням рівняння
- •Вариант 5.
- •1. Описати неокласичні математичні моделі макроекономіки.
- •2. Складний пуассонівський процес можна представити у вигляді:
- •3. Нехай та - квадратично-інтегровані -мартингали.
- •Вариант 6.
- •1. Сформулювати та доказати варіант теореми Леві для вінеровського процесу.
- •2. Стохастичний інтеграл Іто зі змінною верхньою межею є:
- •3. Використовуючи формулу Іто, довести, що:
- •Вариант 7.
- •1. Описати конструктивне завдання пуассонівського процесу.
- •2. У стохастичному диференціалі відсутній коефіцієнт зносу. У формулі Іто в загальному випадку присутні:
- •3. Нехай - узагальнений пуассонівський процес, де відомі параметри: , , - інтенсивність пуассонівського процесу . Знайти для математичне очікування та дисперсію.
- •Вариант 8.
- •1. Доказати нерівність Колмогорова-Гаєка-Рен'ї для мартінгал-різниць.
- •2. Результатом прорідження пуассонівського потоку вимог з параметром є:
- •3. Нехай – рішення наступного рівняння
- •Вариант 9.
- •1. Описати властивості збереження субмартінгальності у марківські моменти часу.
- •2. Ціна в рівнянні р. Белмана повинна мати наступні властивості гладкості:
- •3. Вирішити стохастичне диференціальне рівняння:
- •Вариант 10.
- •10. Вивести рівняння р. Беллмана.
- •2. Випадкові величини, що фігурують у розкладанні вінерівського процесу в ряд, мають розподіл:
- •3. Нехай на завдано потік -алгебр і випадкова величина , що має скінченне математичне очікування. Показати, що випадкова функція є мартінгалом стосовно .
- •Вариант 11
- •1. Вивести балансове рівняння у задачі р. Мертона із споживанням.
- •2. Прирощення стандартного вінерівського процесу розподілені за:
- •3. Нехай – послідовність незалежних однаково розподілених випадкових величин з та . Показати, що послідовність є мартингалом відносно фільтрації , породженої послідовністю .
- •Вариант 12.
- •1. Описати конструктивне завдання вінеровського процессу.
- •2. Які величини входять у балансове рівняння задачі р.Мертона зі споживанням:
- •3. Знайти та , якщо .
- •Вариант 13.
- •1. Описати та доказати властивості стохастичного інтегралу з випадковою верхньою межею.
- •2. Які величини входять у балансове рівняння для терминальної плати задачі р.Мертона:
- •Вариант 14.
- •1. Вивести балансове рівняння у задачі р. Мертона без споживання.
- •2. Якщо модель еволюції фінансового активу має властивість безарбітражності, то яке з тверджень є вірним:
- •3. Нехай - рішення рівняння
- •Вариант 15.
- •1. Доказати незалежність прирощень пуасонівського процесу
- •2. Стохастичний інтеграл Іто є інтегралом:
- •3. Довести, що , якщо - стандартний вінерівський процес.
- •Вариант 16.
- •1. Доказати властивість Бакстера.
- •2. У сумах Іто значення інтегруємої функції береться:
- •3. Довести формулу дифференціювання добутку двох випадкових процессів:
- •Вариант 17.
- •1. Сформулювати та доказати узагальнення узагальненої формули Іто.
- •2. У стохастичному диференціалі відсутня дифузійна частина. У формулі Іто в загальному випадку присутні:
- •Вариант 18.
- •1. Знайти оптимальні управління та ціну керування в задачі Мертона із споживанням (інтегральний критерій).
- •2. Фінансовий актив х має властивість безарбітражності. Яке з тверджень є вірним:
- •3. Нехай - незалежні однаково розподілені випадкові величині такі що: для кожного . Нехай . Показати, що є -мартингалом для кожного .
- •Вариант 19.
- •1. Сформулювати та доказати узагальнену формулу Іто для стохастичних диференціалів.
- •2. Стандартний вінерівський процес є:
- •3. Доказати, що узагальнений пуассонівський процес , де відомі параметри: , , - інтенсивність пуассонівського процесу , має незалежні прирощення.
- •Вариант 20.
- •1. Доказати нерівність Лундебрга.
- •3. Показати, що однорідний пуасонівський процес є субмартингалом відносно та припускає представлення виду де - мартингал відносно , а - детермінована функція
- •Вариант 21.
- •Вариант 22.
- •Проверим на безарбитражность модель Самуэльсона. Для этого найдём .
- •2. Якщо за деякою ймовірносною мірою модель має властивість безарбітражності, то за деякою еквівалентною мірою модель:
- •3. Нехай задовольняють наступній системі рівнянь
- •Вариант 23.
- •1. Доказати нерівність а. Н. Колмогорова для позитивних субмартінгалів. (включаючі зауваження)
- •2. Якщо в моделі Самуельсона , то процес ціноутворювання є:
- •3. Знайти закон розподілу випадкової величини . Виявити, чи усякий рівень може бути подоланий. Якщо так, то скільки в середньому доведеться чекати моменту настання цієї події.
- •Вариант 24
- •1. Сформулювати поняття арбітражу. Привести достатні умови безарбітражності.
- •Рассмотрим – приращение цены, где – цена в момент времени , Модель будет безарбитражной, если
- •2. Характеристика стандартного вінерівського процесу дорівнює:
- •3. Довести , якщо - супермартінгал, - марківський момент часу, що приймає значення на множині всіх раціональних точок проміжку .
- •Вариант 25.
- •1. Описати модель Кларка та перевірити її на безарбітражність.
- •2. Якщо та , то яке з наведених тверджень є вірним:
- •3. Перевірити, чи є випадковий процес рішенням стохастичного диференціального рівняння , , де - невипадковий параметр.
2. Складний пуассонівський процес можна представити у вигляді:
Ответ: б) стохастичного інтегралу;
3. Нехай та - квадратично-інтегровані -мартингали.
а)
Якщо
 та
та
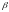 – дійсні числа, показати, що для
будь-якого цілого
– дійсні числа, показати, що для
будь-якого цілого
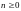
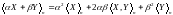
б) Доказати нерівність
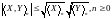
Решение: а) Из определения квадратичной интегрируемости, квадратической ковариации и взаимной характеристики мартингалов, получаем
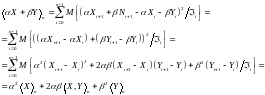
б)
Из того, что квадратическая вариация
всегда положительная и, используя
результат из пункта а), получаем для
любого
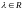 :
:
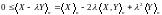
Пусть
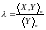 ,
тогда
,
тогда
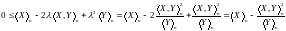
Откуда следует
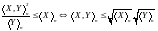 .
.
Вариант 6.
1. Сформулювати та доказати варіант теореми Леві для вінеровського процесу.
Теорема
(Вариант теоремы Леви
для винеровского процесса).
Пусть процесс
определен при
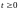 ,
,
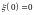 ,
и для всех
определены σ-алгебры
,
и для всех
определены σ-алгебры
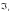 ,
причем
,
причем
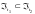 при
при
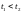 .
Если выполнены условия:
.
Если выполнены условия:
для всех величина
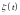 измерима относительно
;
измерима относительно
;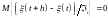 с
вероятностью, равной единице, для всех
и
с
вероятностью, равной единице, для всех
и
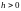 ,
то есть процесс
– мартингал относительно потока
;
,
то есть процесс
– мартингал относительно потока
;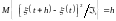 с
вероятностью, равной единице, для всех
и
;
с
вероятностью, равной единице, для всех
и
;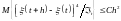 ,
,
тогда является винеровским процессом.
Доказательство.
Вычислим
условное математическое ожидание
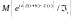 .
Покажем, что верно
.
Покажем, что верно
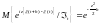 ,
(1)
,
(1)
откуда
очевидным образом вытекает, что
является винеровским процессом.
Положим
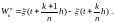
В
силу того, что
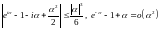 при
при
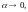 имеем
имеем
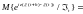
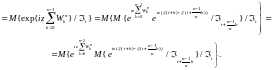 (2)
(2)
В силу того, что
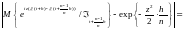
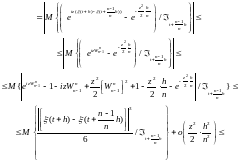
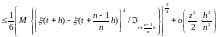
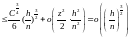 .
.
Из (2) следует, что

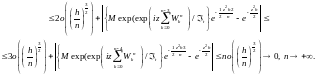
То
есть,
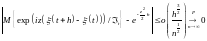
Таким образом, (1) имеет место. Теорема доказана.
2. Стохастичний інтеграл Іто зі змінною верхньою межею є:
Ответ: а) мартингалом
3. Використовуючи формулу Іто, довести, що:
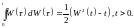
Решение:
Пусть
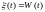 ,
тогда
удовлетворяет стохастическому
дифференциальному уравнению
,
тогда
удовлетворяет стохастическому
дифференциальному уравнению
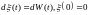 .
Рассмотрим процесс
.
Рассмотрим процесс
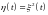 ,
тогда используя формулу Ито для функции
,
и учитывая, что
,
тогда используя формулу Ито для функции
,
и учитывая, что
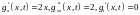 ,
получаем:
,
получаем:
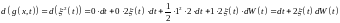
Т.е.
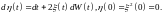 Переходя к интегральной записи, получаем:
Переходя к интегральной записи, получаем:
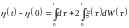
Откуда
с учетом
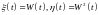 ,
получаем:
,
получаем:
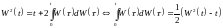 .
.
Вариант 7.
1. Описати конструктивне завдання пуассонівського процесу.
Пусть
наблюдается поток исков, поступивших
в страховую компанию за промежуток
времени
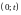 :
:

0 τ1 τ1+τ2 τ1+…+τn t τ1+τ2+…+τn+τn+1
Обозначим
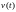 – число исков, поступивших в страховую
компанию за промежуток времени
,
моменты
– число исков, поступивших в страховую
компанию за промежуток времени
,
моменты
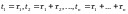 – моменты наступления страховых событий,
причем
– моменты наступления страховых событий,
причем
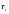 – независимые одинаково распределенные
случайные величины, имеющие экспоненциальное
распределение с параметром
– независимые одинаково распределенные
случайные величины, имеющие экспоненциальное
распределение с параметром
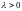 ,
то есть
,
то есть
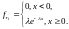
Найдем вероятность того, что на интервале поступит ровно требований, то есть
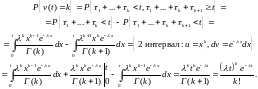
Введем теперь считающий поступления требований процесс :





0 τ1 τ1+τ2 τ1+…+τk
То есть на интервале от нуля до поступления первого требования он равен нулю, на следующем интервале – единице и т.д., то есть в любой момент времени равно числу требований, поступивших в компанию за промежуток времени .
Вероятность
того, что за промежуток времени
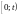 поступит ровно
требований, таким образом, равна
поступит ровно
требований, таким образом, равна
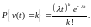
Процесс
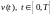 ,
называется процессом Пуассона.
,
называется процессом Пуассона.
2. У стохастичному диференціалі відсутній коефіцієнт зносу. У формулі Іто в загальному випадку присутні:
Ответ: а) частинна похідна за t, частинна похідна за х і друга частинна похідна за х;
