Вариант 1.

1. Сформулювати та доказати узагальнену формулу Байєса

Пусть выполнено:

,

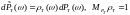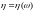– измерима относительно -алгебры ,

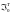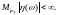
Тогда, если 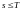, то верно следующее равенство (обобщенная формула Байеса):

.

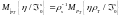Доказательство.

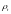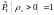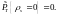Так как является процессом плотности, то отсюда следует, что , т.е. Пусть 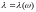– ограниченная 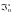-измеримая случайная величина и , тогда

.

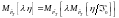С другой стороны, так как 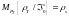, следует

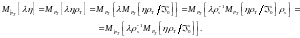
Приравняем выражения в скобках:

,

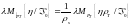откуда следует

.

2. Математичне очікування та дісперсія процесу Пуассона дорівнюють відповідно.

Ответ: в) 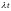і ;

3. Оцінити наступну ймовірність

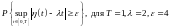
де 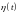– однорідний пуасонівський процес з інтенсивністю .

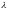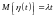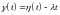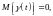
Решение. Так как , то процесс является центрированной случайной функцией с независимыми приращениями, причем 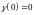. Пусть 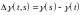для 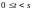. Покажем, что 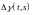не зависит от -алгебры 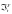. Для этого достаточно показать независимость указанного приращения от произвольного набора сечений 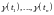, где 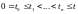. Поскольку эти сечения можно представить в виде линейного преобразования приращений 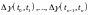, то требуемое утверждение следует из того, что эти приращения не зависят от , т.к. 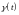- процесс с независимыми приращениями. Теперь в силу независимости от , находим

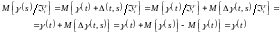
Откуда следует, что – мартингал. Теперь, учитывая что 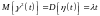(так как – пуассоновский процесс), то воспользуемся неравенством Колмогорова:

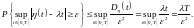
Отсюда при 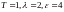получаем

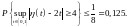
Последнее означает, что с вероятностью, не меньшей 0,875, максимальное отклонение реального числа скачков процесса от ожидаемого числа 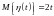на промежутке времени 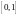будет не больше 4.

Вариант 2.

1. Описати зв'язок потіка Ерланга з пуассонівським процесом.

Если пуассоновский поток «прореживать» так, что сохраняется каждая k-тая точка, а все промежуточные выбрасываются, то такой поток называется потоком Эрланга k-того порядка.

Нетрудно заметить, что требования в таком потоке будут поступать через время 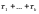. Хорошо известно, что плотность величины имеет вид

,

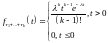причем

, .

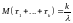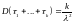Обозначим через 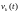эрланговский поток требований k-го порядка. Найдем распределение для . Пусть 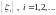последовательность независимых одинаково распределенных случайных величин с плотностью

.

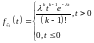Тогда

,

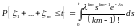а

.

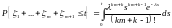Таким образом,

.

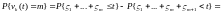
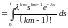
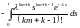Интегрируя последний интеграл k раз по частям, получим

.

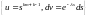
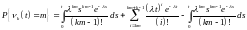Следовательно,

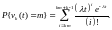
2. Якщо в моделі Самуельсона μ > 0, то процес ціноутворювання є:

Ответ: б) субмартингалом;

3. Нехай – незалежні однаково розподілені випадкові величини з для деякого . Нехай позначає їх часткові суми. Показати, що

а) 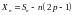є мартингалом;

б) 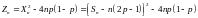є мартингалом.

Решение: Начнем с того, что заметим что:

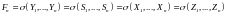
а) Для начала посчитаем

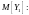
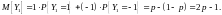
Так как 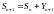, то

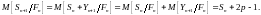
Учитывая вышесказанное и используя тот факт, что 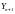и 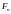- независимы, получаем:

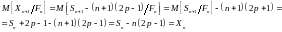
Откуда следует, что 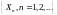является мартингалом.

б) Заметим что мы можем записать 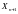как:

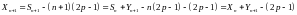
Тогда

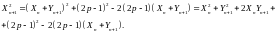
Таким образом, получаем

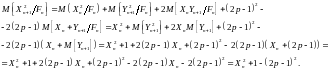
Учитывая все вышесказанное, получаем

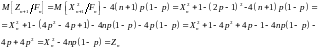
Откуда получаем, что 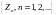является мартингалом.

Вариант 3.

1. Описати прорідження пуассонівського потоку вимог.

Результатом «прореживания» пуассоновского потока требований с параметром является пуассоновский поток требований с параметром .

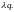Пусть каждое требование в пуассоновском потоке либо сохраняется, либо исключается. 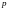– вероятность того, что требование будет исключено. Реально такая ситуация возможна, если ущерб от аварии 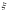меньше франшизы d (размеры выплат независимы от потока требований 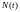и одинаково распределены).

Вероятность того, что на интервале 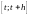будет предъявлено ровно 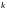требований, равна:

,

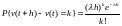тогда вероятность того, что на интервале будет предъявлено ровно одно требование:

;

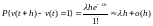более, чем одно требование:

;

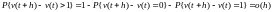требования на этом интервале времени предъявляться не будут:

.

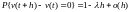Пусть А – событие, состоящее в том, что требование будет сохранено, то есть этот иск будет оплачен. Рассмотрим событие 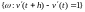, которое состоит в пересечении двух событий .

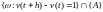В силу того, что событие A и t являются независимыми, имеем

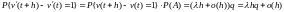
и

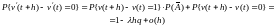
Положим 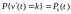, тогда

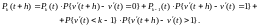(11)

Подставляя в (11) значения соответствующих вероятностей, получим

,

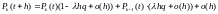откуда

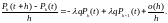(12)

Из (12), учитывая то, что 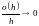при 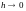равномерно относительно t, находим

.

Положим 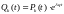, тогда

, ,

,

, ,

,

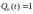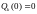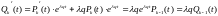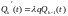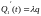
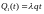
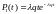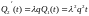
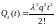
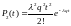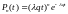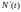то есть _, т.е. «прореженный» пуассоновский процесс действительно будет процессом Пуассона с параметром .
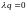