56. Бір қалыпты жинақты болатын тізбек пен қатардың негізгі қасиеттері

1. Теорема (шексіз функцияның үзіліссіздігі). Егер [а,b] кесіндідегі үзіліссіз функциялар тізбегі U₁(X), U₂(X),…U_n(X)…осы кесіндіде бірқалыпты U(X)функциясына жинақталатын болса, онда U(X) функциясы [а,b] кесіндісінде үзіліссіз функция болады.

2. Теорема.Мүшелері [а,b] кесіндісінде үзіліссіз бірқалыпты жинақты болатын қатардың қосындысы осы кесіндіде үзіліссіз функция болады.

3. Теорема. Кесіндідегі шектеулі үзіліссіз функциялардың қосындысы осы кесіндіде үзіліссіз функция болады

57.Функционалдық қатардың дифференциалдануы Егер 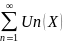қатар мүшелері [а,b] кесіндісінде үзіліссіз дифференциалданып және қатар осы кесіндіде U(X) функциясына жинақталатын болса, ал 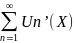қатар бірқалыпты жинақталса, онда оның қосындысы S’(X)функциясына тең болады.

S’(X)=

( )=

Егер қатар кесіндісінде (4) түріндегі қатысты қанағаттандырып дифференциялдауға болады.

58. Функционалдық қатардың интегралдануы Егер үзіліссіз функциялар қатары U₁(X), U₂(X),…U_n(X)… [а,b] кесіндісінде бірқалыпты U(X) функциясына жинақталатын болса онда сандық қатар

жинақты және оның шегі 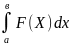интегралына тең болады.

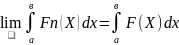
Теорема.Мүшелері [а,b] кесіндісінде үзіліссіз болатын бірқалыпты жинақталатын қатарды осы кесіндіде мүшелеп интегралдауға болады. Яғни [а,b] кесіндісінде қатар мүшелерінің интегралынан құрылған қатар осы кесіндідегі қатар қосындысының интегралына жинақталады.

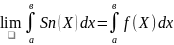
59.Дәрежелік қатар, оның жинақтылығы.Абель теоремасы Мына түрдегі берілген қатарды

(1)

дәрежелік қатар деп аталады.

нақты айнымалысы.

Мұн: а – қайсыбір тұрақты сан

Абель теоремасы: Егер (1) түрде дәрежелік қатар мәнінде жинақталатын болса, онда ол мына теңдікті 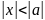қанағаттандыратын х – тің барлық мәнінде абсолютті жинақты болады.

Егер 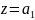нүктесінде дәрежелік қатар жинақсыз болып немесе абсолютсіз жинақталатын болса, онда ол мына

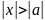
теңсіздікті қанағаттандыратын х – тің барлық мәнінде абсолютті жинақсыз болады.

60. Дәрежелік қатардың жинақталу интервалы және радиусы мысал Егер нүктесі дәрежелік қатардың жинақталу нүктесі болса онда 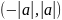интервалы қатардың барлық жинақталу нүктелерінен тұрады.

интервалы дәрежелік қатардың жинақталу интервалы, ал саны жинақталу радиусы деп аталады.

Дәрежелік қатардың жинақталу радиусын мына формула арқылы пайдаланамыз.

Мысал: 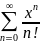қатардың анықталу облысын табайық. пайдаланамыз.

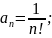
қатар абсолютті жинақты.

61. Дәрежелік қатарды дифференциалдау.мысал 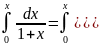(1)

Дәрежелік қатар интервалында жинақты болсын; сонда (1)ді мүшелеп дифференциялдау арқылы

осы қатарды аламыз.

Теорема: Дәрежелік қатарды жинақталу интервалында мүшелеп дифференциялдауға болады. Егер

болса, онда

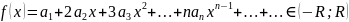
1. Салдар Дәрежелік қатарды жинақталу интервалында соншалықты рет дифф-лдауға болады, яғни

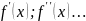
2. Салдар. Дәрежелік қатар қосындысы жинақталу интервалында шексіз көп дифф-данатын функция болады.

Анықтама: Егер функциясы жинақталу интервалындағы нүктеде немесе интервалдың өзінде кез келген ретте дифф-лданса онда функцияны шексіз көп дифф-данатын функция деп атайды.

62. Дәрежелік қатарды интегралдау.мысал Теорема: Дәрежелік қатарды жинақталу интервалында жататын кез келген кесіндісінде мүшелеп интегралдауға болады. Бұл жағдайда да дәрежелік қатар ды 0-ден x- қа дейін мүшелеп интегралдауға болады. Бұл жағдайда

Мысал. Дәрежелік қатарды мүшелеп интегралдаудың мысалы ретінде және функциясының дәрежелік қатарға жіктеуін қарастырамыз.

-тің орнына қойып мына түрдегі теңдікті аламыз.

немесе

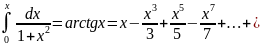теңдігін аламыз.

63.Тейлор және Маклорен қатары Егер 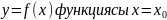нүктелер аймағында -дін ретке дейін қоса алғанда туындыларға ие болса, онда

сияқты. 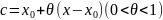нүктелері бар болады. Бұл формула нүктелер үшін 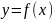функцияларының Тейлор формуласы деп, ал 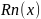Лагранж формуласындағы Тейлор формуласының қалдық мүшесі деп айтады.

Көп мүше.

функциялардың Тейлор көп мүшесі деп аталады.

кезінде формуланың

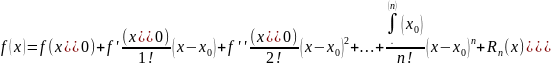
дербес жағдайына келеміз

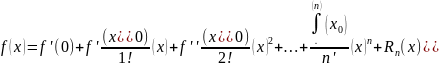
Бұл формула функциясының Маклорен формуласы деп аталады.