37.Жоғрағы ретті тұрақты коэффицентті сызықты біртекті емес дифференциалдық теңдеу(1-теорема) Жоғарғы ретті тұрақты коэффициентті сызықты біртекті емес дифференциалдық теңдеу. (1-теорема)
(1)
Мұн:
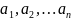тұрақты
нақты коэффициенттер f(x)-(a,b)
аралығындағы
үзіліссіз функция
1
–теорема. Егер (1)-дің оң жағындағы
функция мына түрде берілсе
Мұн:
- дәрежесі «m» болатын көпмұшелік, онда
(1)-дің дербес шешімі
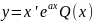түрінде ізделінеді.
Бұл жерде екі жағдайды ескеру керек.
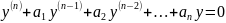
Егер
α мінезедемелік
еселі түбірі болса, онда дербес шешім
түрінде
ізделінеді
38.Жоғарғы ретті тұрақты коэффицентті сызықты біртекті емес дифференциалдық теңдеу(2-теорема) 2-теорема. Егер -тің оң жағы мына түрде берілсе
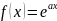
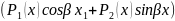
Мұн:
,
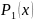– дәрежелері
сәйкес
болатын
көпмүшеліктер онда (1)-дің дербес шешімін
(3)
түрінде іздеуімізге болады.
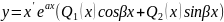
Мұн
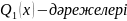m-нен
үлкен
болмайтын көпмүшеліктер (
қанша
рет түбірі болатындығын көрсетеді
39.
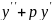+qy=0 теңдеуі берілген.Мінездемелік
теңдеудің түбірлері k1,k2 нақты әр түрлі
шешімін жаз.мысал
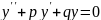
Мұн:
–
тұрақты нақты сандар
Бұл
теңдеудің жалпы интегралын табу үшін
, екі еселі сызықты тәуелсіз дербес
шешімдерін табу жеткілікті.
,
мұн:
k=const
Сонда:
, 
болады.
Енді:
y,
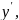→ (1)
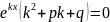
Мінездемелік
теңдеудің екі түбірі
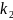бар.
Осы түбірлерге байланысты әртүрлі
жағдайлар болуы мүмкін.
Егер
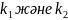–нақты сандар және
Мысал:
,
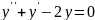мінездемелік теңдеу
,
,
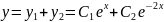теңдеудің жалпы шешімі
40.
+qy=0 теңдеуі берілген.Мінездемелік
теңдеудің түбірлері k1,k2 нақты, қайталанбалы
K1=K2 (Жалпы шешімін жаз, мысал)
Мұн: – тұрақты нақты сандар
Бұл теңдеудің жалпы интегралын табу үшін , екі еселі сызықты тәуелсіз дербес шешімдерін табу жеткілікті. , мұн: k=const
Сонда: , болады.
Енді: y, → (1)
Егер
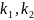–нақты сандар және
бұл жағдайда түбір екі еселі
, 
, 
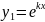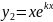және т.с.с.
Мысал:
,
,
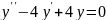(екі
еселі түбір)
, 
,
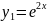жалпы шешім
41. +qy=0 берілген.Мінездемелік теңдеудің түбірлері k1,k2 түйіндес комплексті (Жалпы шешімін жаз, мысал) (1)–екінші ретті сызықты теңдеу
Мұн: – тұрақты нақты сандар
Бұл теңдеудің жалпы интегралын табу үшін , екі еселі сызықты тәуелсіз дербес шешімдерін табу жеткілікті. Дербес шешімдерін мына түрде іздейміз.
, мұн: k=const
Сонда: , болады.
Енді: y, → (1)
Мінездемелік теңдеудің екі түбірі бар. Осы түбірлерге байланысты әртүрлі жағдайлар болуы мүмкін.
Егер түйіндес комплексті түбірлер болса,
,
; 
,
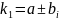онда
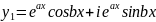
Мысал:
, 
Мұн:
, 
, 
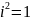
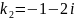
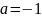
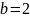
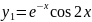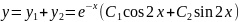
42.Екінші ретті сызықты, біртекті емес дифференциалдық теңдеу, оның жалпы шешімі.Теорема Екінші ретті сызықты емес теңдеу
Теорема:
(1) түріндегі біртекиі емес теңдеудің
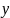жалпы шешімін осы теңдеудің қайсыбір
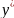дербес шешімін және сол теңдеуге
сәйкес
Біртекті
теңдеудің
жалпы
шешешімінің қосындысы түрінде көрсетуге
болады, яғни
43. Екінші ретті сызықты, біртекті емес дифференциалдық теңдеудің дербес шешімін табудың Логранж әдісі Лагранж әдісі немесе тұрақытыны вариациялау әдісі
Осы теңдеудегі дербес шешімі мына түрде қарастырылады.
,
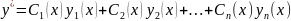
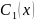функцияларын
төмендегі жүйеден табамыз.
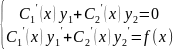теңдеудің
анықтауышы
; 
; 
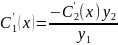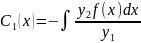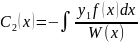
44.Сандық қатар. Дербес және қатар қосындысы. Қатардың жинақты және жинақсыз негізгі қасиеттері Мына түрдегі өрнекті
(1)
Сандық қатар деп аталады.
Мұн:
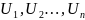– қатар мүшелері
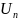– қатардың жалпы мүшесі.
Анықтама: Қатардың алғашқы n мүшесінің қосындысы n- дербес қосындысы деп аталады.
Дербес қатарлардың тізбегі.
Яғни
Анықтама: Егер (3) түрдегі тізбектің шектеулі шегі бар болатын болса, онда ол шекті (1) қатардың қосындысы деп аталады.
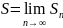
Бұл жағдай қатарды жинақталатын н/е жинақты қатар д.а.
Мысалы:
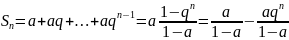
сонда,
a)
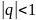болса,
- қатар жинақты
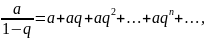
Егер
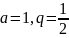болса,
онда
+…+
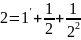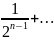
б)
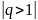бұл жағдайда қатар жинақсыз, себебі
в) q=1, q= -1. Болғанда сәйкес мына түрдегі қатарларды ала аламыз.
-
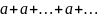қатар
жинақсыз.себебі:
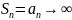
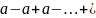
Негізгі
қасиет: 1. Егер (1) түрдегі қатар жинақты
болып және оның қосындысын S болса, онда
мына қатарды
(c=const) жинақты, және оның қосындысын C,S
болады.
2.
Егер қатарлар
,
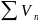жинақталатын болып және олардың сәйкес
қосындылары болып
боолса, онда мына қатарда
жинақты қосындысы
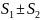болады.
3. Егер (1) түрінде қатар шектеулі мүшелерді қосқаннан шығатын қатар мен (1) түріндегі қатардың жинақтылығы да, не жинақсыздығы да бірдей
45.
Сандық қатар жинақтылығының қажетті
және жеткілікті шарттары.мысал Теорема
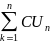түрдегі қатар жинақты болса, онда осы
жалпы мүшесінің шегі нолге ұмтылады
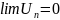
Айталық
(1) түріндегі жинақты болсын және
.
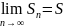Бұл жағдайда
,
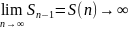онда
. 
екендігін ескеріп
,
деп теңдікті ала аламыз.
Мысал: Қатарды жинақтылыққа зерттейік.
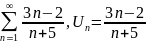
46.Қатар жинақтылығың зерттеудегі Даламбер белгісі.мысал).Егер дәрежелік қатар х-тің барлық дәрежелерін қамтымаса, яғни тікелей берілген қатар мүшелернің модульдерінен құралған қатар үшін Даламбер белг арқылы табамыз. Мыс:Қатардың 1-1/3*3+1/5*32-1/7*33+…+(-1)n-11/(2n-1) анықталу обл болып табылады .Қатар толық қатар емес. Бұл жағдайда Даламбер белгісін пайдаланамыз.