
- •1.Алғашқы функция және анықталмаған интеграл, оның негізгі қасиеттері?
- •2.Анықталмаған интегралда айнымалыны ауыстыру тәсілі (дәлелдеу)
- •9. . Тригонометриялық функцияның интегралы(мысал келтір)
- •10.Тригонометриялық функцияның интегралы (мысал келтір)
- •11. Тригонометриялық функцияның интегралы мысал
- •12. Тригонометриялық функцияның интегралы мысал
- •16.Ньютон-Лейбниц формуласы.Теорема
- •17.Анықталған интегралда айнымалыны ауыстыру.Дәлелдеу
- •37.Жоғрағы ретті тұрақты коэффицентті сызықты біртекті емес дифференциалдық теңдеу(1-теорема) Жоғарғы ретті тұрақты коэффициентті сызықты біртекті емес дифференциалдық теңдеу. (1-теорема)
- •47. Қатар жинақтылығың зерттеудегі Коши радикалдық белгісі.Мысал
- •48. Қатар жинақтылығың зерттеудегі Кошидің интегралдық белгісі
- •49.Қатарларды салыстыру белгісі.Мысал
- •56. Бір қалыпты жинақты болатын тізбек пен қатардың негізгі қасиеттері
1.Алғашқы функция және анықталмаған интеграл, оның негізгі қасиеттері?
Егер кесіндісінің барлық нүктелерінде мына
тендік орындалатын боса,
кесіндісінің барлық нүктелерінде мына
тендік орындалатын боса,
 (x)=f(x)
онда
(x)
f(x) фун-ң
кесіндегі алғашқы
функциясы
д.а. Мысал; f(-x)-F(x)-? Алғашқы ф-ң анықтамасы
бойынша мына функция F(x)=
(x)=f(x)
онда
(x)
f(x) фун-ң
кесіндегі алғашқы
функциясы
д.а. Мысал; f(-x)-F(x)-? Алғашқы ф-ң анықтамасы
бойынша мына функция F(x)= ,f(x)=
,f(x)= кіші функцияның алғашқы функциясы
болады. f(x)=(F(x)
кіші функцияның алғашқы функциясы
болады. f(x)=(F(x)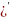 =(
=(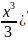 =
=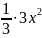 =
.
Ескерту:
Егер f(x)=
ф-сы үшін алғашқы ф-я бар болатын боса,
онда алғашқы функция жалғыз болмайды.
Мысал: 1) F(x)=
2)F(x)=
+2,
(x)=
+0=
,F(x)=
-7,
=
.
Ескерту:
Егер f(x)=
ф-сы үшін алғашқы ф-я бар болатын боса,
онда алғашқы функция жалғыз болмайды.
Мысал: 1) F(x)=
2)F(x)=
+2,
(x)=
+0=
,F(x)=
-7,
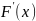 =
-0=
Сонымен жалпы түрде алғашқы фунецияны
мына түрде жаза аламыз; F(x)=
+c-тұрақты
сан.Анықтама: егер
F(x) ф-сы, f(x) ф-ң алғашқы ф-сы болатын боса,
онда мына түрдегі өрнек F(x)+c
өрнекті
ф-я анықталмаған интегралы д.а
=
-0=
Сонымен жалпы түрде алғашқы фунецияны
мына түрде жаза аламыз; F(x)=
+c-тұрақты
сан.Анықтама: егер
F(x) ф-сы, f(x) ф-ң алғашқы ф-сы болатын боса,
онда мына түрдегі өрнек F(x)+c
өрнекті
ф-я анықталмаған интегралы д.а
 dx=F(x)+C
dx=F(x)+C
 белісі f(x)-
белісі f(x)-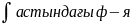 ,
f(x)dx-
,
f(x)dx- стындағы
өрнек, х-ф-я айнымалысы. Негізгі
қасиеттері: 1) Анықталмаған
интеграл туындысы
стындағы
өрнек, х-ф-я айнымалысы. Негізгі
қасиеттері: 1) Анықталмаған
интеграл туындысы
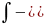 астындағы ф-ға тең. (
астындағы ф-ға тең. (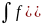 )dx
=(F(x)+c
=
(x)+0=f(x).
2)Анықталмаған
ың
диф-лы
астындағы
өрнекке тең d(
)dx
=(F(x)+c
=
(x)+0=f(x).
2)Анықталмаған
ың
диф-лы
астындағы
өрнекке тең d( (x)dx)=f(x)dx
яғни d(
(x)dx)=(
(x)dx
dx=f(x)dx.
3) Қайсыбір ф-я диф-лы
лы
сол ф-ға қосылған тұрақтыға тең
(x)dx)=f(x)dx
яғни d(
(x)dx)=(
(x)dx
dx=f(x)dx.
3) Қайсыбір ф-я диф-лы
лы
сол ф-ға қосылған тұрақтыға тең
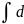 (F(x))=F(x)+C
бұл теңдіктің шындығына көз жеткізу
үшін, теңдіктің 2 жағын бірдей диф-у
керек. 4)
(F(x))=F(x)+C
бұл теңдіктің шындығына көз жеткізу
үшін, теңдіктің 2 жағын бірдей диф-у
керек. 4)
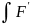 (x)dx=F(x)+C
5)
(x)dx=F(x)+C
5)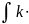 f(x)dx=k
(x)dx
k=const 6)
f(x)dx=k
(x)dx
k=const 6)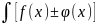 dx=
(x)dx
dx=
(x)dx dx
dx
2.Анықталмаған интегралда айнымалыны ауыстыру тәсілі (дәлелдеу)
Айталық
(x)dx
анықталмаған
ң
бірдей алғашқы ф-сын табу қиынға соқсын,
бірақта ал
ң
бар болатындығы бізге белгілі болсын.
Бұл жағдайда
 өрнекте
айнымалыны ауыстырамыз. Ескерту;
дың
соңында t-бойынша алынған
өрнекте
айнымалыны ауыстырамыз. Ескерту;
дың
соңында t-бойынша алынған
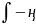 нәтижесі х арқылы өрнектеліп жазылады.
Дәлелдеу; Шындығында айталық F(x)-f(x) ф-ң
алғашқы ф-сы болсын, яғни
(x)=f(x).
Сонда F(
нәтижесі х арқылы өрнектеліп жазылады.
Дәлелдеу; Шындығында айталық F(x)-f(x) ф-ң
алғашқы ф-сы болсын, яғни
(x)=f(x).
Сонда F( (t))
ф-сы мына ф-ң алғашқы ф-сы болады.
(
)dx
=(F(x)+c
=
(x)+0=f(x)
формуланы анықталмағанда
да
айнымалыны ауыстыру формуласы д.а.
Ескерту; Кейбір
(t))
ф-сы мына ф-ң алғашқы ф-сы болады.
(
)dx
=(F(x)+c
=
(x)+0=f(x)
формуланы анықталмағанда
да
айнымалыны ауыстыру формуласы д.а.
Ескерту; Кейбір
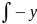 жағдайында айнымалыны ауыстыру мына
түрде t=f(x) болғаны ыңғайлы болады. Мысал
үшін, егер
жағдайында айнымалыны ауыстыру мына
түрде t=f(x) болғаны ыңғайлы болады. Мысал
үшін, егер
 dx-?
онда f(x)=t
dx-?
онда f(x)=t
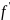 (x)dx=dt
болады. Сонда
(x)dx=dt
болады. Сонда
 =
= =ln
=ln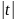 +c=f(f(x))+c.
Мысал
+c=f(f(x))+c.
Мысал
 =
= =
=ln
+c=ln
=
=ln
+c=ln +c
+c
3.Анықталмаған интегралды бөліктен интегралдау тәсілі (мысал келтір)
Айталық
U=U(x),
V=V(x)
-
екі ф-ны диф-цал ф-я босын. Екі ф-ң
көбйтіндісінің диф-лы, мына формулаламен
есептеледі; d(U V)=udv+vdu
түріңдегі теңдіктің 2 жағын бірдей
интегралдацық онда
(U
v)=
V)=udv+vdu
түріңдегі теңдіктің 2 жағын бірдей
интегралдацық онда
(U
v)=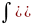 duv+vdu)=
duv+vdu)= dv+
dv+ du.
Сонда;
uv=
dv+
du
н\е
dv=uv
du.
Сонда;
uv=
dv+
du
н\е
dv=uv du
du
4.Квадрат
үш мүшелігі бар функцияның интегралы
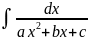
Мына
түрдегі
интегралды
қарастырайық. Алдын ала бөлшектің
бөліміндегі авадрат үшмүшелікті
түрлендірейік; a
+bx+c=a(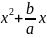 +
+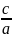 )=a(
+
)=a(
+ x+(
x+( +
-(
+
-(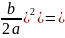 a
a =a
=a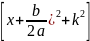 Мысалж;
Мысалж;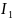 =
=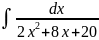 =
= =
=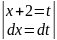 =
=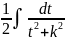 =
=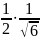 arctg
arctg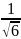 +c=
+c=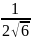 arctg
arctg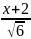 +c
+c
5.
Квадрат үш мүшелігі бар функцияның
интегралы
 dx
dx
 dx
түріндегі
ды
қарастырайық. инг астынғы
өрнекті тепе-теңдік жағдайына түрлендіреміз
dx=
dx
түріндегі
ды
қарастырайық. инг астынғы
өрнекті тепе-теңдік жағдайына түрлендіреміз
dx= dx=
dx=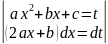 =
= -
- =ln
+c=
ln
=ln
+c=
ln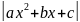 +c
+c
 (B-
(B-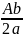 )
=(B-
)-
)
=(B-
)-
Р1 мен Р2 табылған мәндерін орындарына қойып I2 ны табамыз.
6.
Квадрат үш мүшелігі бар функцияның
интегралы
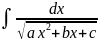 dx
dx
Мына
түрдегі
интегралды
 =
dx
қарастырайық 1-ші
жағдайда түрлендірудің көмегімен бұл
интеграл табылғн интегралға келтіреді.
=
dx
қарастырайық 1-ші
жағдайда түрлендірудің көмегімен бұл
интеграл табылғн интегралға келтіреді.
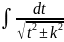 =ln
=ln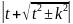 +c,
a
0
н\е
.
+c,
a
0
н\е
.
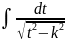 =arcsin
=arcsin +c,
a
+c,
a
7.
Квадрат үш мүшелігі бар функцияның
интегралы
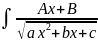 dx
dx
 =
dx
түріндегі
интегралды 2-ші жағдайда қарастырылған
түрлендіру арқылы;
=
dx=
=
dx
түріндегі
интегралды 2-ші жағдайда қарастырылған
түрлендіру арқылы;
=
dx= dx+(B-
dx+(B-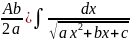 =P+(B-
)
=P+(B-
) P=
dx=
=
P=
dx=
=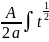 dt=
2
dt=
2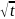 +c=
+c=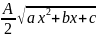 +c Мысал;
+c Мысал; =;
=; =
=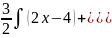 =
= dx-5
dx-5 =3
=3 -5ln
+c
-5ln
+c
8.Анықтамалары (..................) Дұрыс және дұрыс емес бөлшектер. Оларды интегралдау (мысал келтір)
Анықтама;егер
бөлшектің алымының дәрежесі бөлімінің
жәрежесіне кіші боса, онда бөлшек дұрыс
бөлшек деп, ал кері жағдайда бөлшек
дұрысемес бөлшек д.а. Ескерту; Егер
бөлшек дұрыс емес бөлшек боса, онда
бөлшектің алымын бөліміне бөлу арқылы
көпмүшеліктерді бөлу ережесі бойынша,
берілген бөлшекті көпмүшеліктер мен
дұрысбөлшектің қосындысы түрінде
көрсетуімізге болады.
 =M(x)
+
=M(x)
+ ,
мұнда М(x)-көпмүшелік,
-
дұрыс бөлшек. Мысал Бізге дұрыс емес
бөлшек берілген
,
мұнда М(x)-көпмүшелік,
-
дұрыс бөлшек. Мысал Бізге дұрыс емес
бөлшек берілген
 (m=4,n=2) Бөлшектің алымын бөліміне бөлеміз.
(m=4,n=2) Бөлшектің алымын бөліміне бөлеміз.
